
Урок "Формулы приведения"

Краткое описание документа:
Видеоурок «Формулы приведения» вспомогательный материал для обеспечения наглядности учебной информации при объяснении темы на школьном уроке. Формулы приведения – важная тема, знание которой необходимо для решения тригонометрических задач при последующем изучении геометрии. Однако запомнить формулы и научиться правильно применять достаточно сложно. Поэтому желательно применение учителем вспомогательных инструментов, повышающих эффективность данного урока. В ходе видеоурока ученики знакомятся с понятием формулы приведения, различными группами формул, рассматривают примеры по их использованию в решении задач.
Использование наглядного материала, способствующего запоминанию информации, желательно при изучении данной темы. В видеоуроке используется выделение цветом, демонстрация рисунков и таблиц для обеспечения наглядности материала и его запоминания. С помощью голосового сопровождения пособия делаются важные комментарии для понимания материала.
Видеоурок начинается с представления названия темы. Дается определение формул приведения на примере тригонометрической функции, под которой выражение πn/2±t. Отмечается, что вид этой функции можно несколько упростить таким образом, что под знаком функции останется только аргумент t. Определение как важный аспект выделено в рамку и рекомендовано для запоминания. Чтобы облегчить ученикам запоминание формул приведения, в видео рекомендуется принять к сведению мнемонические правила.
В первом правиле отмечается, что для формул приведения, где тригонометрическая функция содержит выражения вида π+t, π-t, 2π+t, 2π-t, в этом случае тригонометрическая функция сохраняет наименование. Второе правило отмечает закономерность для тригонометрических функций, в которых содержится сумма аргументов вида π/2±t, 3π/2±t, в этом случае наименование функции изменится на родственное, то есть синус меняется на косинус или наоборот, а также тангенс на котангенс и наоборот. Еще одно правило направляет ученика на установку правильного знака в функции. Отмечается, что для аргумента 0<t<π/2 перед результирующей функцией ставится знак, как у исходной функции.
Отмечается справедливость формул приведения при указании в них углов в градусной мере, помимо радианной меры. То есть формулы приведения можно использовать, если встречаются выражения 90°+α, 90°-α, 180°+α и т.д.
Далее рассматривается применение формул приведения. Это помогает усвоить учебный материал. Отмечается, что ранее была доказана формула cos(π+t)=- cost, но пользуясь формулой приведения, можно произвести преобразование более быстро. Для этого в правой части экрана напоминается правило преобразования функции, формулы приведения для функции вида π+t. Заметим, согласно правилу, что наименование функции, косинус, сохраняется. Для установки правильного знака указывается, в какой части координатной плоскости располагается угол. На рисунке изображена координатная плоскость, на которой единичная окружность разделена на четыре части с названиями – I, II, III, IV. Ниже напоминается табличная информация о знаке функций синуса и косинуса в зависимости от четверти. Согласно имеющимся данным, находим знак косинуса данного угла - это минус. Согласно изученному мнемоническому правилу, знак минус ставится перед функцией, поэтому cos(π+t)=- cost.
Во втором примере необходимо преобразовать формулу sin(π/2+t). В правой части экрана напоминается правило для преобразования формул, содержащих аргумент вида π/2±t. Согласно формулам, название функции меняется на родственное, то есть на косинус. Чтобы определить знак результирующей функции, демонстрируется единичная окружность на координатной плоскости, разбитая на четверти. Отмечается, что данный угол при 0<t<π/2 будет располагаться во второй четверти. Ниже приводится таблица, в которой можно найти знак функции в данной таблице – плюс. Поэтому после применения формулы приведения выражение получает вид sin(π/2+t)= cost.
В следующем примере рассматривается преобразование выражения tg(3π/2+t). Справа от выражения на экране напоминается соответствующее правило из формул приведения о наименовании функции. Применив данное правило, отмечаем, что наименование функции меняется на котангенс. Далее рассматривается знак результирующего выражения. Правило установки знака отмечено в правой части экрана. Для выбора правильного знака на рисунке напоминается расположение четвертей координатной плоскости и таблица знаков тригонометрических функций в данных четвертях. Согласно табличным данным, для угла, расположенного в четвертой четверти, перед функцией необходимо установить знак минус. В результате преобразования получаем tg(3π/2+t)= ctgt.
Далее рассматриваемые примеры несколько усложняются, отмечая, что формулы приведения применимы и для более сложных выражений. Для преобразования дано выражение ctg(360°+у/2). Аналогично уже рассмотренным примерам, для данного примера напоминается соответствующее правило по выбору наименования функции. Согласно нему, так как 360° - это 2π, наименование функции сохраняется – котангенс. Так как рассматриваемый угол лежит в первой четверти, а, согласно таблице, в этой четверти знак котангенса - плюс, то и перед выражением останется плюс, то есть преобразованное выражение ctg(360°+у/2)= ctg у/2.
Рассматривается пример применения формулы приведения для вычисления значения sin(-330°). Сначала используем нечетность данной функции для вынесения минуса из под знака функции. Соответствующее правило отображается в правой части экрана. Таким образом, sin(-330°)=- sin 330°. Далее представляем аргумент в виде разности с уменьшаемым 360°. Так получаем под знаком функции выражение 360°-30°. Зная, что 360°=2π, пользуясь соответствующим правилом, отмечается сохранение наименования функции. При этом угол, от которого находится синус, находится в четвертой четверти координатной плоскости. Поэтому, согласно таблице, знак перед функцией – минус. Подставляя найденный знак перед функцией, получаем sin(-330°)=-(-sin 30°)=1/2.
В следующем примере необходимо доказать тождество, в котором присутствуют тригонометрические функции, которые можно преобразовать с помощью формул приведения (3 cos 50° - 4 sin 140°)/cos 130°=1. Можно преобразовать используемое в данном тождестве выражение sin 140°. Представив аргумент в виде суммы 140°=90°+50°, можно использовать соответствующую формулу приведения для π/2+t. Очевидно, наименование функции меняется. Так как аргумент 90°+50° находится во второй четверти, а синус в ней имеет знак минус, то перед функцией ставится знак минус. Таким же образом преобразуем cos 130°. Представив аргумент в виде разности 130°=180°-50°, отмечаем, что можно использовать формулу приведения для аргумента вида π-t. Для такого аргумента наименование функции сохраняется. Пользуясь табличными данными определяем, что для угла из второй четверти знак косинуса – минус. Поэтому cos 130°= -cos50°. После подстановки полученных выражений и приведения подобных слагаемых в числителе получаем одинаковые выражения в числителе и знаменателе, дающие в результате 1. Поэтому данное тождество является верным.
Видеоурок «Формулы приведения» может повысить эффективность традиционного урока математики. Также данный материал может быть полезен учителю, осуществляющему дистанционное обучение. Материал можно рекомендовать для самостоятельного рассмотрения отстающим ученикам.
ТЕКСТОВАЯ РАСШИФРОВКА:
Тригонометрическую функцию, под знаком которой содержится выражение вида ± t (пи эн деленное на два плюс минус тэ), где n – целое число, можно привести к более простому виду, такому что под знаком тригонометрической функции будет только аргумент t. Такие формулы обычно называют формулами приведения.
Формул приведения очень много. Можно составить таблицу формул приведения, но пользоваться ею неудобно, так как она очень громоздка.
Чтобы использовать формулы приведения, не заучивая их, полезно знать мнемоническое правило (правило, которое облегчает запоминание):
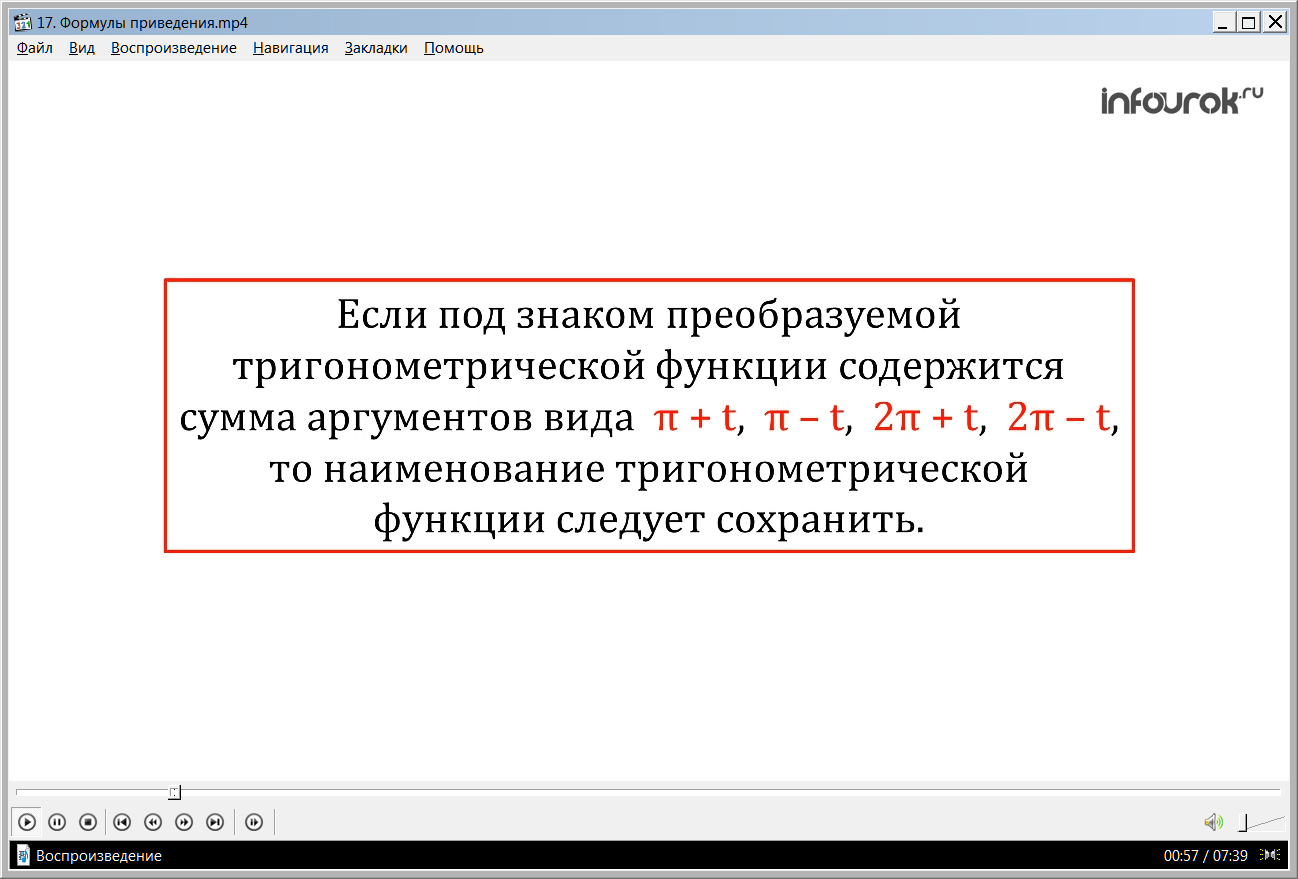
1) Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида π + t, π – t, 2π + t, 2π – t (пи плюс тэ, пи минус тэ, два пи плюс тэ, два пи минус тэ), то наименование тригонометрической функции следует сохранить;
2) Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида + t, – t, + t, – t (пи на два плюс тэ, пи на два минус тэ, три пи на два плюс тэ, три пи на два минус тэ), то наименование тригонометрической функции следует изменить на родственно ( синус меняется на косинус, тангенс на котангенс и наоборот);
3) Перед полученной функцией от аргумента тэ надо поставить тот знак, который имеет исходная функция при условии, что 0< t < ( тэ больше нуля, но меньше пи на два).
Любая из формул приведения может быть записана и для градусной меры угла, то есть когда под знаком тригонометрической функции записано выражение вида 90° + α , 90° - α, 180° + α и т. д.(девяноста градусов плюс альфа, девяноста градусов минус альфа, сто восемьдесят градусов плюс альфа и так далее) .
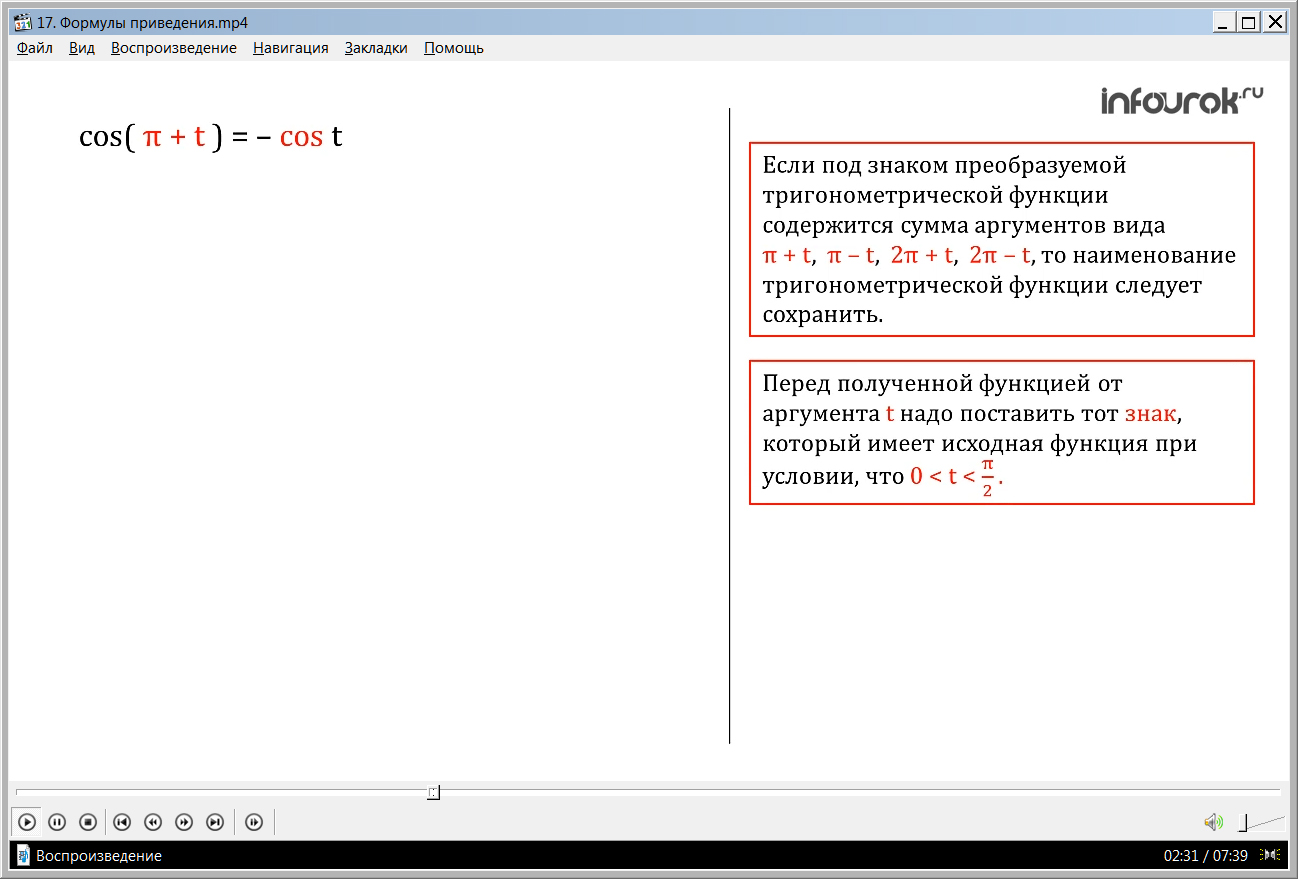
Ранее мы уже доказали формулу: cos( π + t ) = - cost( косинус пи плюс тэ равен минус косинусу тэ). Но ведь к этой формуле можно применить сформулированное выше правило. Преобразуем левую часть формулы :
cos( π + t ) (косинус пи плюс тэ). Наименование функции сохраняется, то есть получаем cost. Далее, если считать, что 0< t < ( тэ больше нуля, но меньше пи на два, то есть тэ – аргумент из первой четверти), то π + t( пи плюс тэ) – аргумент из третьей четверти, а в ней исходная (или преобразуемая) функция косинус имеет знак минус. По правилу этот знак надо поставить перед полученной функцией. Таким образом, cos( π + t ) = - cost( косинус пи плюс тэ равен минус косинусу тэ).
Преобразуем sin ( + t) (синус пи на два плюс тэ). Наименование функции изменяется, то есть получаем косинус тэ. Далее, из того, что 0< t < ( тэ – аргумент из первой четверти), следует, что + t ( пи на два плюс тэ) – аргумент из второй четверти, а в ней преобразуемая функция синус имеет знак плюс. Этот знак поставим перед полученной функцией. Таким образом,
sin ( + t) = cost ( синус пи на два плюс тэ равно косинусу тэ).
А сейчас получим пару новых формул приведения, воспользовавшись сформулированным правилом.
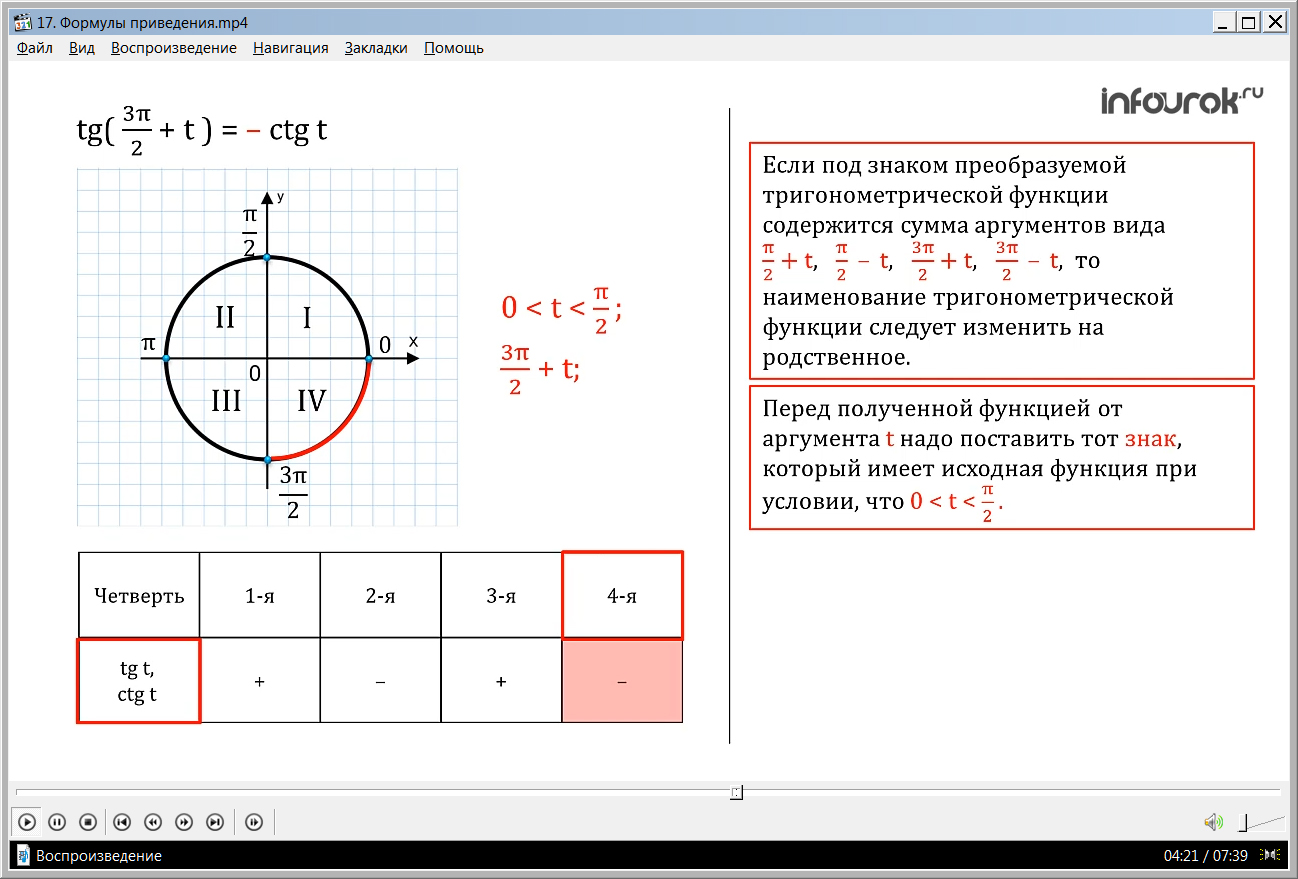
Преобразуем tg ( + t ) (тангенс три пи на два плюс тэ). Наименование функции следует изменить: получим сtg t. Далее, если считать, что 0< t <
( тэ – аргумент из первой четверти), получим, что + t ( три пи на два плюс тэ) – аргумент из четвертой четверти, а в ней преобразуемая функция тангенс имеет знак минус. Этот знак поставим перед полученной функцией. Таким образом, tg ( + t ) = - сtg t (тангенс три пи на два плюс тэ равен минус котангенсу тэ).
Формулы приведения можно применять и в тех случаях, когда вместо аргумента тэ стоит более сложное выражение.
Преобразуем сtg( 360° + )( котангенс триста шестьдесят градусов плюс игрек на два). Наименование функции сохраним (триста шестьдесят градусов равно двум пи): получим сtg ( котангенс игрек на два). Далее, если считать, что 0< t < ( тэ – аргумент из первой четверти), получим, что 360° + (триста шестьдесят градусов плюс игрек на два) – аргумент из первой четверти, а в ней исходная функция котангенс имеет знак плюс. Этот знак надо поставить перед полученной функцией. Таким образом,
сtg( 360° + ) = сtg
( котангенс триста шестьдесят градусов плюс игрек , деленное на два, равен котангенсу игрек, деленное на два).
Рассмотрим пример.
ПРИМЕР. Вычислить с помощью формул приведения sin ( -330° )
(синус от минус трехсот тридцати градусов).
Решение. , Так как для синуса справедливо, что синус от минус тэ равен минус синусу тэ, то sin ( -330°) = - sin 330°.Триста тридцать градусов распишем как разность трехсот шестидесяти и тридцати:
sin ( -330°) = - sin 330° = - sin ( 360° - 30°) .
Наименование функции сохраним. 330° = 360° - 30°- аргумент четвертой четверти, а в ней исходная функция синус имеет знак минус. Этот знак надо поставить перед полученной функцией. Поэтому
sin ( -330°) = - sin 330° = - sin ( 360° - 30°) = - ( - sin 30°)
( синус от минус трехсот тридцати градусов равен одной второй).
ПРИМЕР 2. Докажите тождество
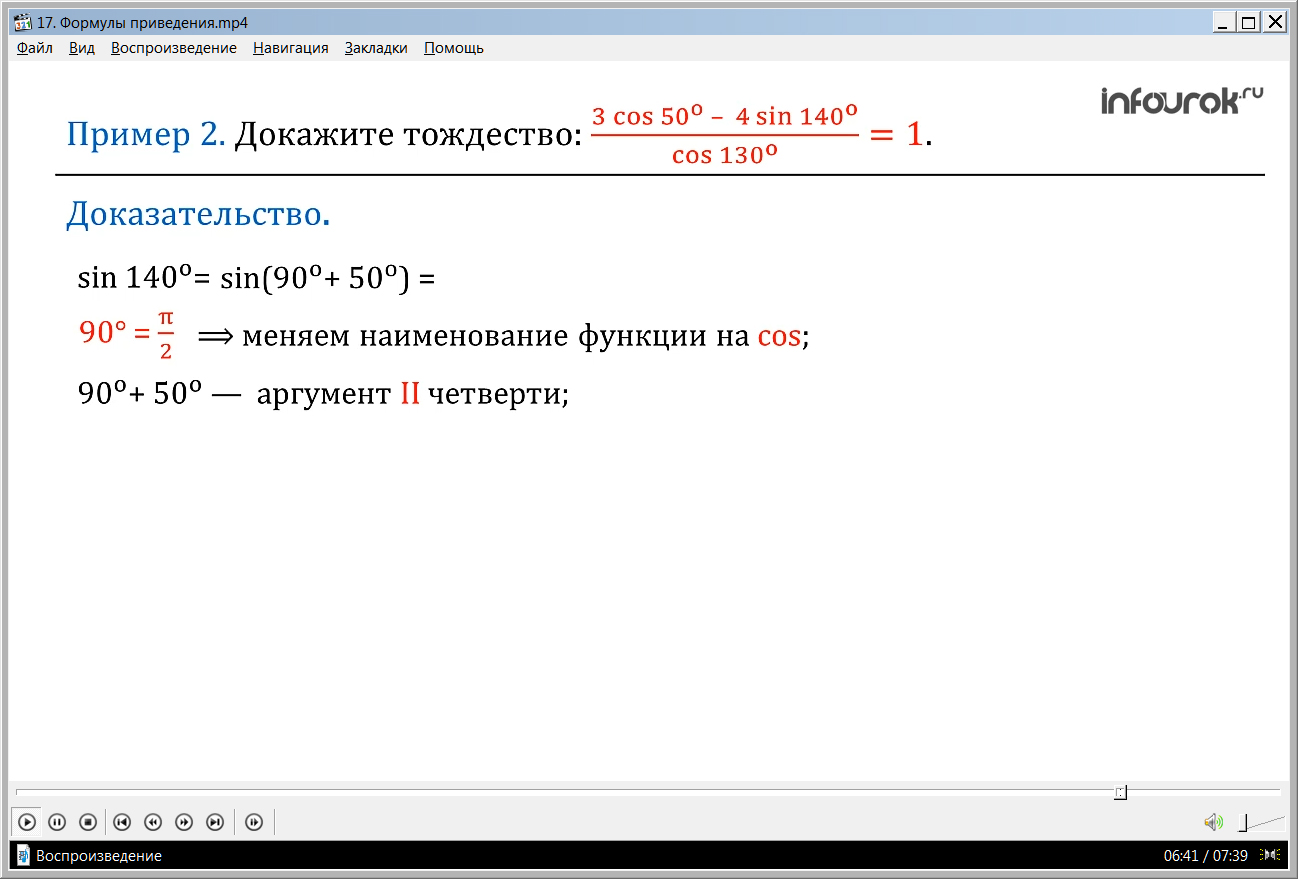
Решение. Используя формулы приведения преобразуем левую часть тождества, а именно в числителе sin 140º= sin(90º+50º)=cos 50º.(синус ста сорока запишем как синус девяноста и пятидесяти, функция изменяется на косинус, так как те 0< t < , то аргумент 90º+50º из второй четверти, знак синуса во второй четверти плюс, тогда получаем косинус 50 градусов)
В знаменателе cos 103º= cos(180º-50º)= –cos50º
(косинус ста тридцати запишем как косинус ста восьмидесяти минус пятьдесят, функция не изменяется (180º), и так как те 0< t < , то аргумент 180º–50º из второй четверти, знак косинуса во второй четверти имеет знак минус, тогда получаем минус косинус 50 градусов)
(Далее в числителе приводим подобные слагаемые получаем минус косинус 50-ти градусов деленное на минус косинус на 50-т градусов получаем единицу).
Тождество доказано.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 13523 |
| Номер материала | 840 |