
Урок "Упрощение тригонометрических выражений"

Краткое описание документа:
Видеоурок «Упрощение тригонометрических выражений» предназначен для формирования навыков у учеников в решении тригонометрических задач с использованием основных тригонометрических тождеств. В ходе видеоурока рассматриваются виды тригонометрических тождеств, примеры решения задач с их использованием. Применяя наглядное пособие, учителю легче достичь целей урока. Яркое представление материала способствует запоминанию важных моментов. Использование анимационных эффектов и озвучивание позволяют полностью заменить учителя на этапе объяснения материала. Таким образом, применяя данное наглядное пособие на уроках математики, учитель может повысить эффективность обучения.
В начале видеоурока объявляется его тема. Затем напоминаются тригонометрические тождества, изученные ранее. На экране отображаются равенства sin2t+cos2t=1, tg t=sin t/cos t, где t≠π/2+πk для kϵZ, ctg t=cos t/sin t, верное для t≠πk, где kϵZ, tg t· ctg t=1, при t≠πk/2, где kϵZ, названные основными тригонометрическими тождествами. Отмечается, что данные тождества часто применяются в решении задач, где необходимо доказать равенство или упростить выражение.
Дальее рассматриваются примеры применения данных тождеств в решении задач. Сначала предлагается рассмотреть решение задач по упрощению выражений. В примере 1 необходимо упростить выражение cos2t- cos4t+ sin4t. Чтобы решить пример, сначала выносится за скобки общий множитель cos2t. В результате такого преобразования в скобках получается выражение 1- cos2t, значение которого из основного тождества тригонометрии равно sin2t. После преобразования выражения очевидна возможность выведения за скобки еще одного общего множителя sin2t, после чего выражение приобретает вид sin2t(sin2t+cos2t). Из того же основного тождества выводим значение выражения в скобках, равное 1. В результате упрощения получаем cos2t- cos4t+ sin4t= sin2t.
В примере 2 также выражение cost/(1- sint)+ cost/(1+ sint) нужно упростить. Так как в числителях обеих дробей находится выражение cost, его можно вывести за скобки как общий множитель. Затем дроби в скобках приводятся к общему знаменателю перемножением (1- sint)(1+ sint). После приведения подобных слагаемых в числителе остается 2, а в знаменателе 1- sin2t. В правой части экрана напоминается основное тригонометрическое тождество sin2t+cos2t=1. Используя его, находим знаменатель дроби cos2t. После сокращения дроби получим упрощенный вид выражения cost/(1- sint)+ cost/(1+ sint)=2/cost.
Далее рассматриваются примеры доказательства тождеств, в которых применяются полученные знания об основных тождествах тригонометрии. В примере 3 необходимо доказать тождество (tg2t-sin2t)·ctg2t=sin2t. В правой части экрана отображены три тождества, которые понадобятся для доказательства - tg t·ctg t=1, ctg t=cos t/sin t и tg t=sin t/cos t с ограничениями. Чтобы доказать тождество, сначала раскрываются скобки, после чего образуется произведение, отражающее выражение основного тригонометрического тождества tg t·ctg t=1. Затем, согласно тождеству из определения котангенса, преобразуется ctg2t. В результате преобразований получается выражение 1-cos2t. Пользуясь основным тождеством, находим значение выражения. Таким образом, доказано, что (tg2t-sin2t)·ctg2t=sin2t.
В примере 4 необходимо найти значение выражения tg2t+ctg2t, если tg t+ctg t=6. Чтобы вычислить выражение, сначала возводится в квадрат правая и левая части равенства (tg t+ctg t)2=62. Формула сокращенного умножения напоминается в правой части экрана. После раскрытия скобок в левой части выражения образуется сумма tg2t+2· tg t·ctg t+ctg2t, для преобразования которой можно применить одно из тригонометрических тождеств tg t·ctg t=1, вид которого напоминается в правой части экрана. После преобразования получается равенство tg2t+ctg2t=34. Левая часть равенства совпадает с условием задачи, поэтому ответ 34. Задача решена.
Видеоурок «Упрощение тригонометрических выражений» рекомендуется применять на традиционном школьном уроке математики. Также материал будет полезен учителю, осуществляющему дистанционное обучение. С целью формирования навыка в решении тригонометрических задач.
ТЕКСТОВАЯ РАСШИФРОВКА:
«Упрощение тригонометрических выражений».
Равенства
1)sin2t + cos2t = 1( синус квадрат тэ плюс косинус квадрат тэ равно одному)
2)tgt =, при t ≠ + πk, kϵZ( тангенс тэ равно отношению синуса тэ к косинусу тэ при тэ не равном пи на два плюс пи ка, ка принадлежит зэт)
3)ctgt = , при t ≠ πk, kϵZ( котангенс тэ равно отношению косинуса тэ к синусу тэ при тэ не равном пи ка, ка принадлежит зэт).
4)tgt ∙ ctgt = 1 при t ≠ , kϵZ (произведение тангенса тэ на котангенс тэ равно одному при тэ не равном пи ка, деленное на два, ка принадлежит зэт)
называют основными тригонометрическими тождествами.
Часто они используются при упрощении и доказательстве тригонометрических выражений.
Рассмотрим примеры использования этих формул при упрощении тригонометрических выражений.
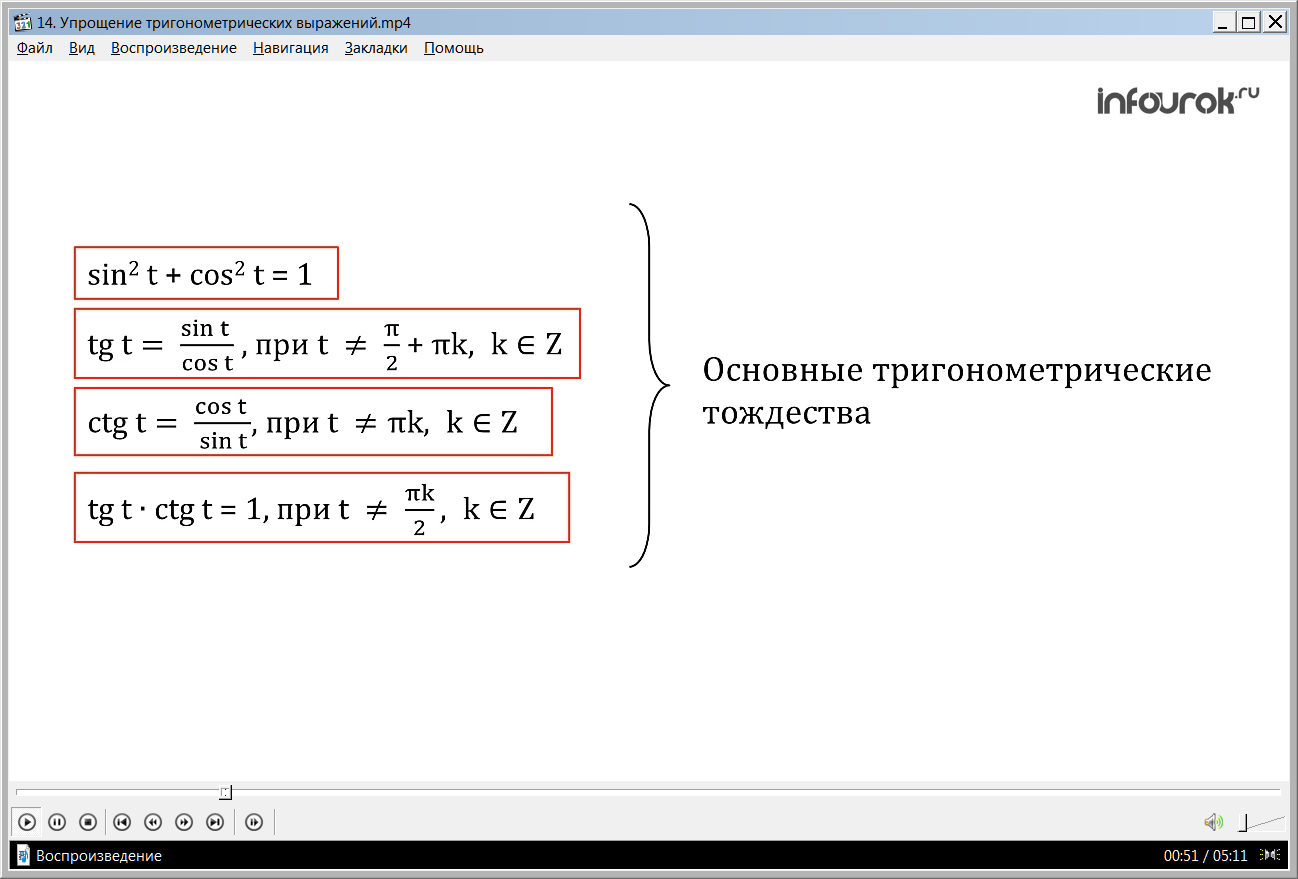
ПРИМЕР 1.Упростить выражение: cos2t – cos4t + sin4t . (выражение а косинус квадрат тэ минус косинус четвертой степени тэ плюс синус четвертой степени тэ).
Решение. cos2 t – cos4 t + sin4 t = cos2 t∙ ( 1 - cos2 t) + sin4 t =cos2 t ∙ sin2 t + sin4 t = sin2 t (cos2 t + sin2 t) = sin2 t·1= sin2 t
( вынесем за скобку общий множитель косинус квадрат тэ, в скобках получим разность единицы и квадрата косинуса тэ, что равно по первому тождеству квадрату синуса тэ. Получим сумму синус четвертой степени тэ произведения косинус квадрат тэ и синус квадрат тэ. общий множитель синус квадрат тэ вынесем за скобки, в скобках получим сумму квадратов косинуса и синуса, что по основному тригонометрическому тождеству равно единице. В итоге получим квадрат синуса тэ).
ПРИМЕР 2.Упростить выражение: + .
(выражение бэ сумма двух дробей в числителе первой косинус тэ в знаменателе единица минус синус тэ , в числителе второй косинус тэ в знаменателе второй единица плюс синус тэ).
( Вынесем общий множитель косинус тэ за скобки, а в скобках приведем к общему знаменателю, который представляет собой произведение один минус синус тэ на один плюс синус тэ.
В числителе получим: единица плюс синус тэ плюс единица минус синус тэ, приводим подобные, числитель равен двум после приведения подобных.
В знаменателе можно применить формулу сокращенного умножения (разность квадратов) и получить разность единицы и квадрата синуса тэ, что по основному тригонометрическому тождеству
равно квадрату косинуса тэ. После сокращения на косинус тэ получим конечный ответ : два деленное на косинус тэ).
Рассмотрим примеры использования этих формул при доказательстве тригонометрических выражений.
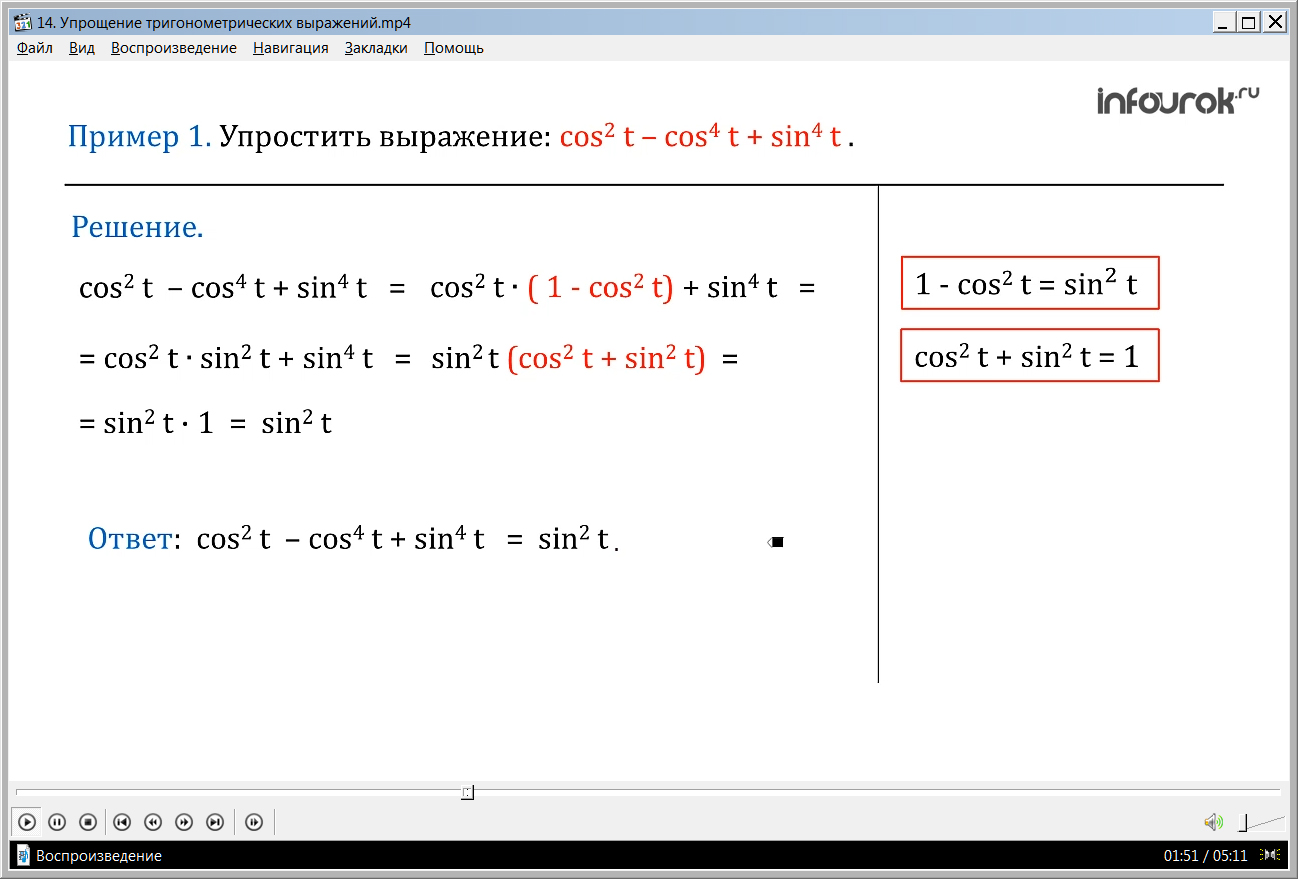
ПРИМЕР 3. Доказать тождество (tg2 t – sin2 t) ∙ ctg2 t = sin 2t (произведение разности квадратов тангенса тэ и синуса тэ на квадрат котангенса тэ равно квадрату синуса тэ).
Доказательство.
Преобразуем левую часть равенства:
(tg2 t – sin2 t) ∙ ctg2 t = tg2 t ∙ ctg2 t - sin2 t ∙ ctg2 t = 1 - sin2 t ∙ ctg2 t =1 - sin2 t ∙ = 1 – cos2t = sin2t
( Раскроем скобки, из ранее полученного соотношения известно, что произведение квадратов тангенса тэ на котангенс тэ равно единице. Вспомним, что котангенс тэ равен отношению косинуса тэ на синус тэ, значит, квадрат котангенса это отношение квадрата косинуса тэ на квадрат синуса тэ.
После сокращения на синус квадрат тэ получим разность единицы и косинуса квадрата тэ, что равно синусу квадрату тэ). Что и требовалось доказать.
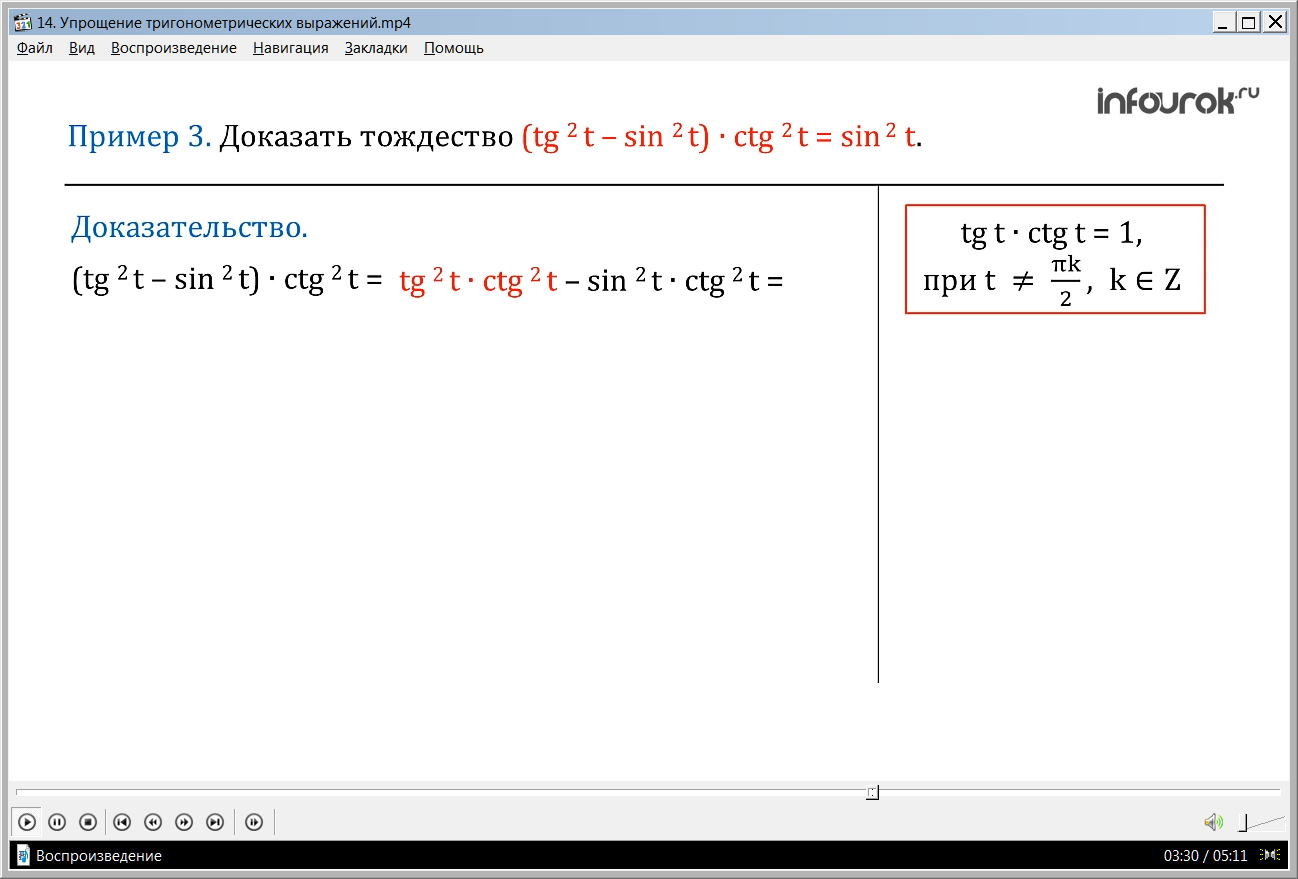
ПРИМЕР 4.Найти значение выражения tg 2 t + ctg2t ,если tgt + ctgt = 6.
( сумма квадратов тангенса тэ и котангенса тэ, если сумма тангенса и котангенса равна шести).
Решение. (tgt + ctgt)2 = 62
tg2 t + 2 ∙ tgt ∙ctgt + ctg2 t = 36
tg 2 t + 2 + ctg 2 t = 36
tg 2 t + ctg 2 t = 36-2
tg2 t + ctg2 t = 34
Возведем обе части исходного равенства в квадрат:
(tgt + ctgt)2 = 62 ( квадрат суммы тангенса тэ и котангенса тэ равна шести в квадрате). Вспомним формулу сокращённого умножения: Квадрат суммы двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй. (a+b)2=a2+2ab+b2 Получим tg2 t + 2 ∙ tgt ∙ctgt + ctg2 t = 36 (тангенс квадрат тэ плюс удвоенное произведение тангенса тэ на котангенс тэ плюс котангенс квадрат тэ равно тридцати шести).
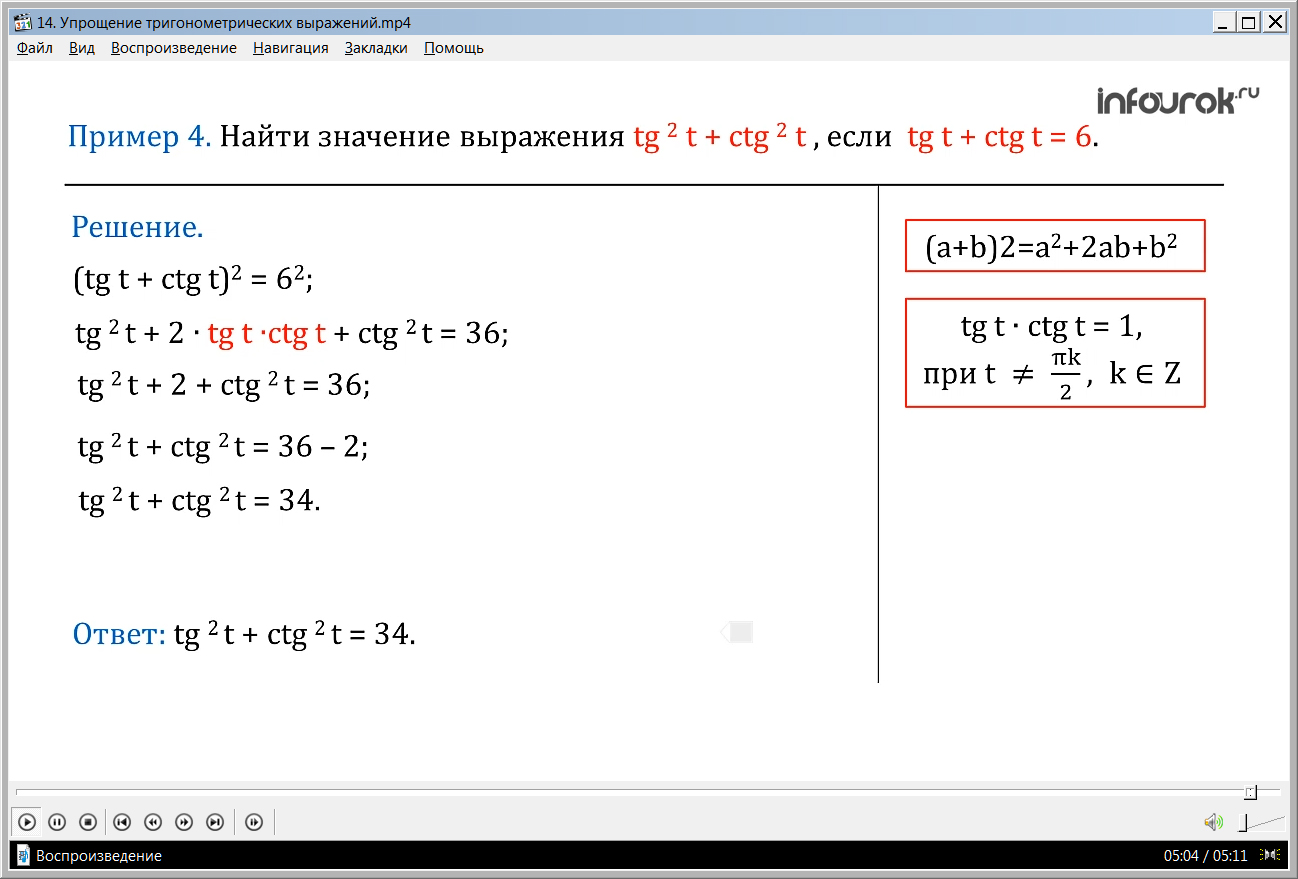
Так как произведение тангенса тэ на котангенс тэ равно единице, то tg2 t + 2 + ctg2 t = 36 ( сумма квадратов тангенса тэ и котангенса тэ и двух равна тридцати шести),
значит tg2 t + ctg2 t = 34 (сумма квадратов тангенса тэ и котангенса тэ равна тридцати четырем). Ответ: 34.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 30794 |
| Номер материала | 837 |