
Урок "Длина дуги числовой окружности"

Краткое описание документа:
В 10 классе изучается числовая окружность. В содержание курса по данной теме входит урок «Длина дуги числовой окружности». Как и любой другой урок по математике, это занятие требует особых средств обучения, которые будут не только наглядными но и наиболее эффективными.
Данный урок длится 7: 11 минут. Примерно столько же времени требуется учителю, чтобы рассказать новый материал обучающимся. Но в этом случае учителю не придется перебирать множество литературы, пересматривать учебники в поиске самого главного по данной теме. Автор данного видеоурока позаботился о свободе учителя, собрал здесь самый свежий, полезный и главный материал.
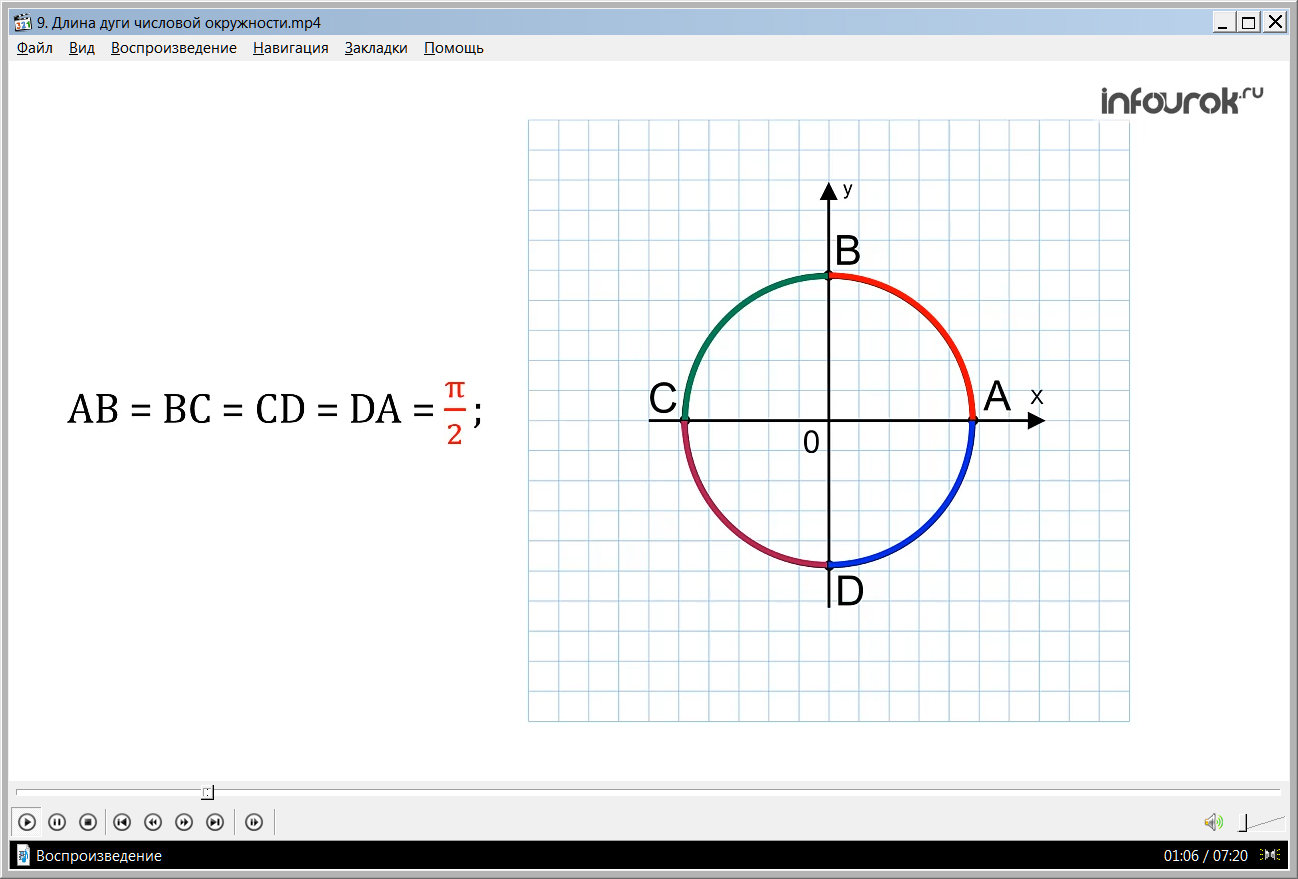
Урок начинается с повторения формулы, по которой находится длина окружности. Но единичная окружность имеет радиус, равный 1, поэтому автор выводит для этого случая свою формулу, вычисляя, в конечном итоге, определенное значение длины числовой окружности. После этого вводится понятие длины дуги числовой окружности на примере единичной окружности.
После рассмотренной теории предлагается закрепить информацию с помощью примера. По условию необходимо найти длины дуг окружности, если в этой окружности проведены два взаимно перпендикулярных диаметра. При этом в задаче есть еще дополнительные сведения, которые помогут более точно найти искомую величину. Пример рассматривается с подробным объяснением решения. Здесь присутствует рисунок, иллюстрирующий суть задачи, математическая запись, развивающая математическую грамотность обучающихся, и логически построенное объяснение каждого этапа решения задачи.
Далее рассматривается не менее наглядный пример, где также необходимо найти длины дуг окружностей. Решение задачи имеет четкую структуру. Здесь имеется иллюстрация. Автор подробно поясняет все, что происходит на экране, все решение, и что, откуда берется.
После этого автор вводит проблему, которую постепенно приводит к решению. Рассказ автора сопровождается иллюстрациями, вся работа отмечается на рисунке, параллельно с этим ведется запись, которая приводит к решению проблемы.
Получив очередную порцию теоретических знаний, обучающимся предлагается рассмотреть пример по этой теории. Здесь необходимо найти, в какой четверти находится точка числовой окружности. И этот пример сопровождается иллюстрациями. Решение расписано подробно, автор комментирует каждое действие, которое происходит на экране.
Здесь урок приходит к завершению. Но на занятии должно оставаться время, чтобы закрепить материал по данной теме. Учителю необходимо подобрать такой материал по способностям обучающихся.
ТЕКСТОВАЯ РАСШИФРОВКА:
Тема нашего урока «ДЛИНА ДУГИ ЧИСЛОВОЙ ОКРУЖНОСТИ»
Известно, что длина окружности L вычисляется по формуле L =2πR (эль равно два пи эр), где π≈3,14 , R – радиус окружности. Для единичной окружности R=1, значит L =2π≈6,28 (эль равно два пи и приблизительно равно шесть целых двадцать восемь сотых).
Следовательно, длина половины дуги окружности АС и BD будет равна π, а длина дуги четверти окружности АВ, BC, СD, DA будет равна .
Рассмотрим примеры на нахождение длины дуги числовой окружности.
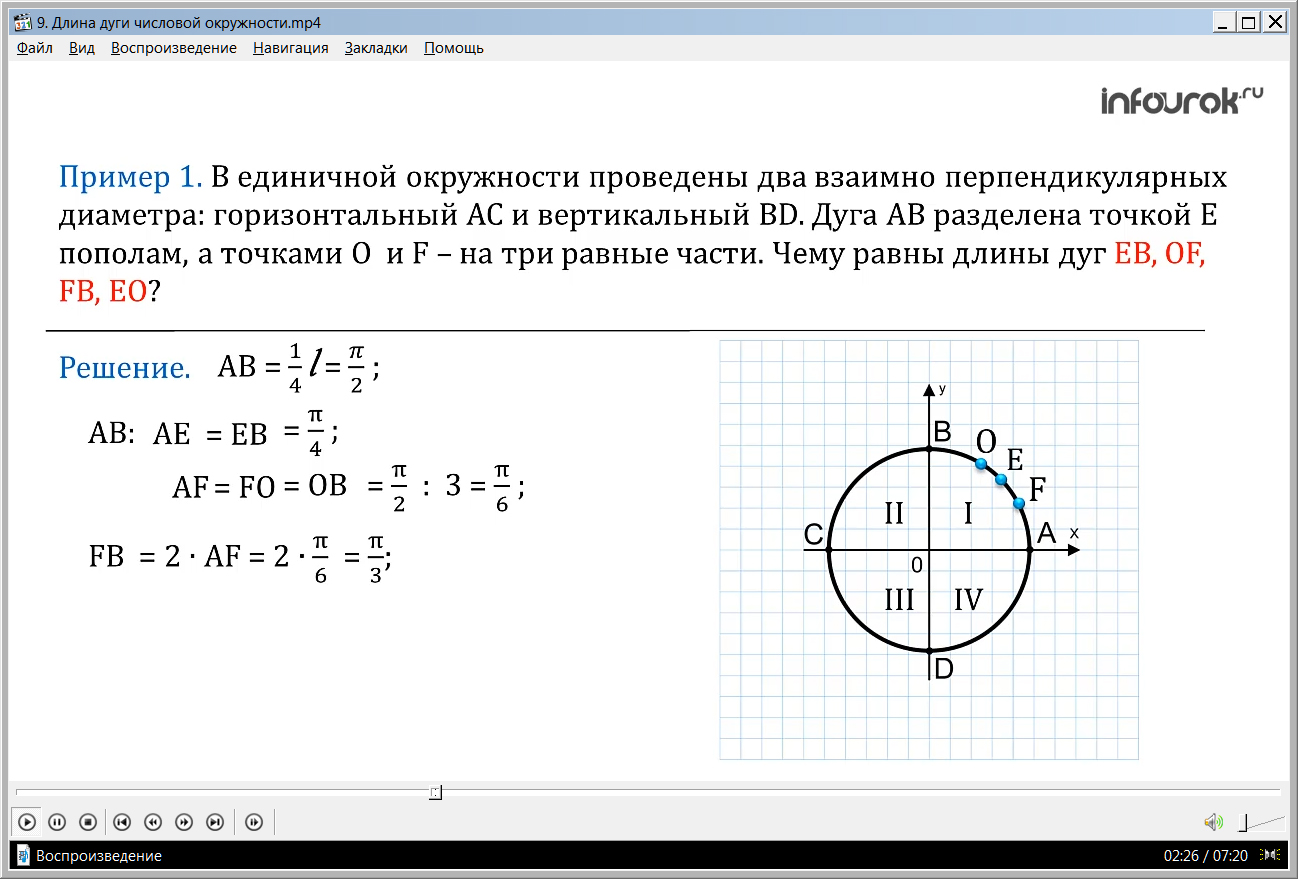
ПРИМЕР 1. В единичной окружности проведены два взаимно перпендикулярных диаметра: горизонтальный СА и вертикальный DB. Дуга АВ разделена точкой Е пополам, а точками O и F – на три равные части
(рис 1). Чему равны длины дуг EВ, OF, FВ, EO?
Решение. Так как дуга АВ – это четвертая часть длины окружности, то ее длина равна . Точкой E дуга АВ была разделена на две равные части, значит, дуги АE и EВ равны, их длины тоже равны. То есть АE = EВ=.
Точками F и O разбили дугу АВ на три равные части, то есть
АF = FO = OВ = ׃ 3 = .( равно пи на два деленное на три равно пи на шесть).
Длину дуги FВ можно найти как удвоенное произведение длины дуги АF .
FВ = 2 ∙ = ( равно два умножить на пи на шесть равно два пи на шесть равно пи на три).
И найдем длину дуги EO. Длину этой дуги можно получить из дуги EВ отбрасыванием дуги OВ. То есть EO = EВ – OВ = –= .( равно пи на четыре минус пи на шесть равно пи на двенадцать).
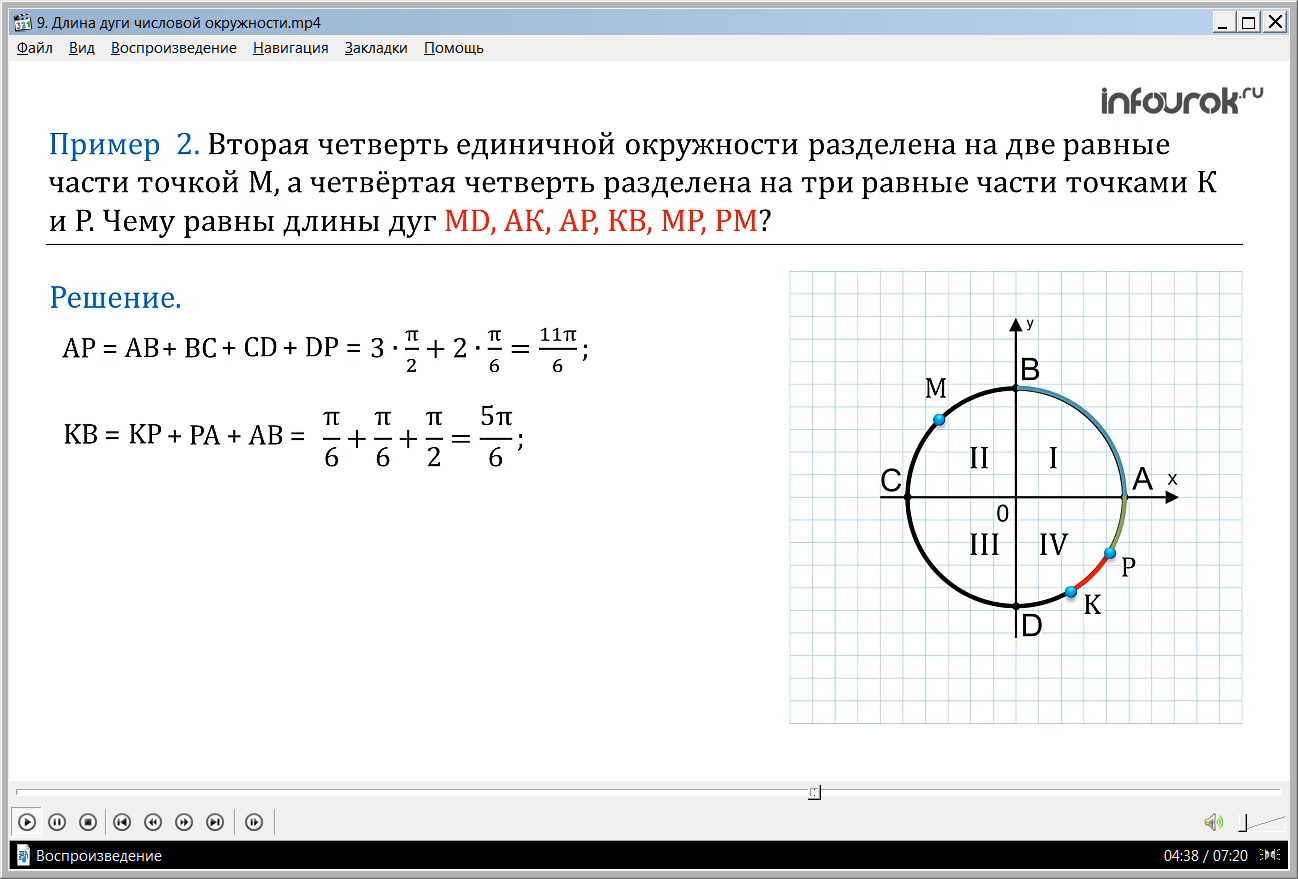
ПРИМЕР 2. Вторая четверть единичной окружности разделена на две равные части точкой М (рис), а четвертая четверть разделена на три равные части точками К и Р. Чему равны длины дуг МD, АК, АР, КВ, МР,РМ?
Решение. Очевидно, что длины дуг АВ, ВС, СD, DА равны между собой и равны пи на два. ВМ равно МС и равно пи на четыре, а DК равно КР равно РА и равно пи на шесть. Следовательно, МD = МС + СD= + = ( эм дэ равно сумме эм сэ и сэ дэ равно сумме пи на четыре и пи на два равно три пи на четыре)
АК = АВ + ВС + СD + DК = + + + = ( а ка равно сумме дуг а бэ, бэ сэ, сэ дэ, дэ ка равно пи на два плюс пи на два плюс пи на два плюс пи на шесть равно пять пи на три)
АР = АВ + ВС + СD + DР= 3∙ +2 ∙ = ( а пэ равно сумме дуг а бэ, бэ сэ, сэ дэ и дэ рэ равно сумме утроенного пи на два и удвоенного пи на шесть равно одиннадцать пи на шесть)
КВ = КР + РА + АВ = + + = ( ка бэ равно сумме дуг ка пэ, рэ а, а бэ рано сумме пи на шесть, пи на шесть и пи на два равно пять пи на шесть)
МР = МС + СD + DК + КР = + + + = ( эм пэ равно сумме дуг эм сэ, сэ дэ, дэ ка, ка пэ равно тринадцать пи на двенадцать)
РМ = РА + АВ + ВМ = + + = ( длина дуги пэ эм равна сумме длин дуг пэ а, а бэ, бэ эм равно сумме пи на шесть , пи на два и пи на четыре равно одиннадцать пи на двенадцать).
В разобранных примерах длины дуг были выражены некоторыми долями числа пи. Это и понятно, ведь длина единичной окружности равна два пи. Возникает вопрос: можно ли найти на единичной окружности такую точку Е1( е один), чтобы длина дуги АЕ1( а е один) была равна 1( единице). Поскольку π ≈ 3,14 ; ≈ 1,05; ≈ 0,79 , то единица больше чем пи на четыре, но меньше, чем пи на три. Рассуждая аналогично, можно найти точку Е2 , чтобы АЕ2 =2 , Е3, чтобы АЕ3=3 и т. д. Приблизительно отметим эти точки на единичной окружности , предварительно разделив каждую из четвертей на три равные части (рис.)
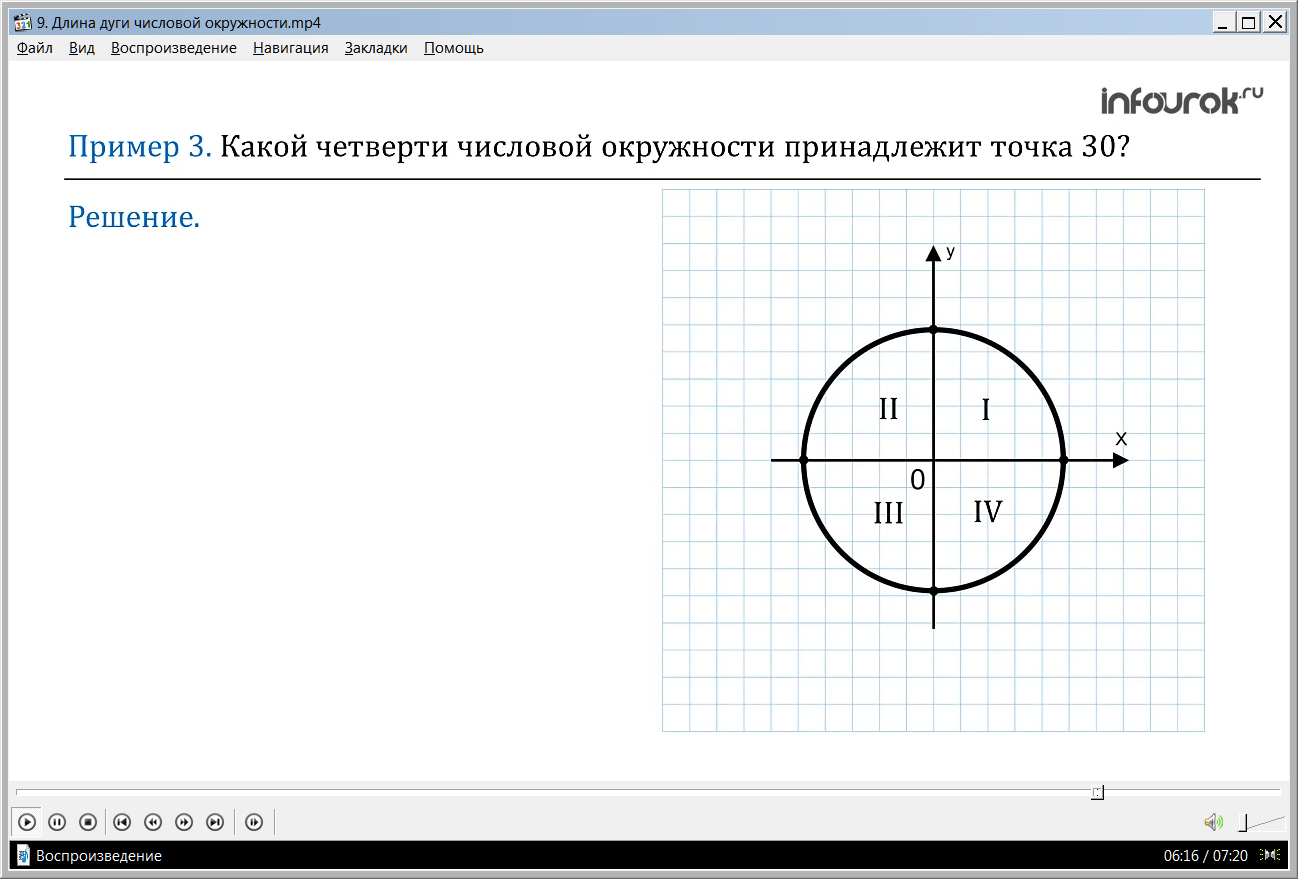
ПРИМЕР 3. Какой четверти числовой окружности принадлежит точка 30?
Решение. Нужно представить число 30 в виде t + 2πk (тэ плюс два пи ка) и подберем значение ка так, чтобы число тэ попало в отрезок [ 0, 2π] ( от нуля до двух пи включая эти числа). Поскольку 2π≈ 6,28 и 2πk ≈ 6,28k (два пи приблизительно равно шесть целых двадцать восемь сотых и два пи ка приблизительно равно шесть целых двадцать восемь сотых ка), то надо подобрать целое число k(ка) так, чтобы число шесть целых двадцать восемь сотых ка оказалось как можно ближе к числу 30. Очевидно, что ка равно четыре. Значит, 30 = 4,88 + 6,28 ∙ 4 (тридцать равно четыре целые восемьдесят восемь сотых плюс шесть целых двадцать восемь сотых, умноженное на четыре). Точка 4,88 находится в четвертой четверти, значит и точка 30 принадлежит четвертой четверти.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 11612 |
| Номер материала | 832 |