
Урок "Вычисление тангенса и котангенса"

Краткое описание документа:
Видеоурок «Определение тангенса и котангенса» представляет наглядный материал для формирования навыков решения задач, в которых используются понятия тангенса и котангенса. В ходе видеоурока рассматриваются определения этих функций, описывается решение множества примеров, в которых употребляется понятие тангенса и котангенса. В видеоуроке просто и понятно разъясняются методы решения подобных задач. Учитывая то, что материал озвучен и даются полезные комментарии, видео способствует лучшему пониманию учебного материала. Данное пособие помогает повысить эффективность обучения, улучшить запоминание материала, быстрее освоить навыки решения задач по теме.
Видеоурок начинается с представления названия темы и определения тангенса и котангенса. В рамке выделено определение тангенса, которое указывает, что тангенс формируется отношением синуса числа на его косинус tg t=sin t/cos t, где t≠π/2+πk для kϵZ. Далее представлено определение котангенса как отношения синуса числа на его косинус ctg t=cos t/sin t, верное для t≠πk, где kϵZ. Определение также выделено в рамке для запоминания. Для этих функций составляется таблица знаков, которые принимают функции в различных четвертях координатной плоскости. Соответственно, в первой и третьей четвертях знак этих функций будет положительным, во второй и четвертой четвертях они имеют отрицательное значение.

Далее представляются примеры, которые демонстрируют решение заданий с использованием изученного материала. В первом примере необходимо вычислить tg π/3. В правой части экрана отображается формула, напоминающая определение тангенса. Зная определение тангенса, преобразуем tg π/3= (sin π/3)/(cos π/3). Используя табличные данные для подстановки значений косинуса и синуса, находим искомое числовое значение tg π/3=√3/2:1/2=√3. Задача решена.
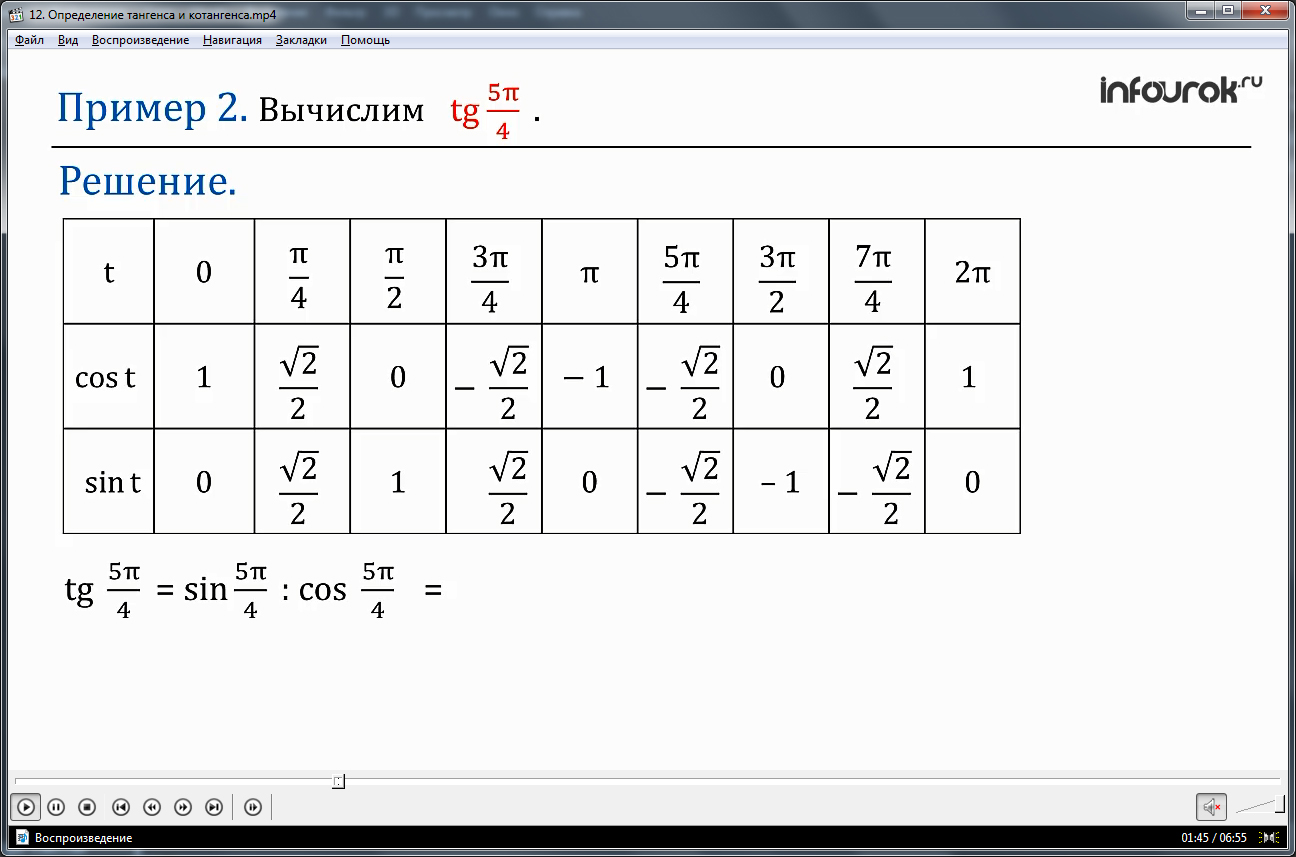
Во втором примере вычисляется значение выражения tg 5π/4. Используя определение тангенса, записываем формулу tg 5π/4= (sin 5π/4)/(cos 5π/4). Значения синуса и косинуса 5π/4 извлекаем из таблицы значений. На экране отображается соответствующая таблица. С помощью анимационных эффектов демонстрируется поиск соответствующего значения. Подставляем найденные значения в формулу -√2/2:(-√2/2)=1. Найденное решение tg 5π/4=1.
Третий пример аналогичен второму. В нем необходимо найти ctg 3π/2. Для решения этого примера необходимо вспомнить определение котангенса. В правой части экрана отображается формула, рассмотренная в начале урока. В соответствии с этой формулой преобразуем исходное выражение ctg 3π/2=(cos 3π/2)/(sin 3π/2). Чтобы найти решение выражения, из таблицы значений косинусов и синусов извлекаем нужные значения. Так как cos 3π/2=0, а sin 3π/2=-1, то их отношение равно 0. Найденное значение ctg 3π/2=0.
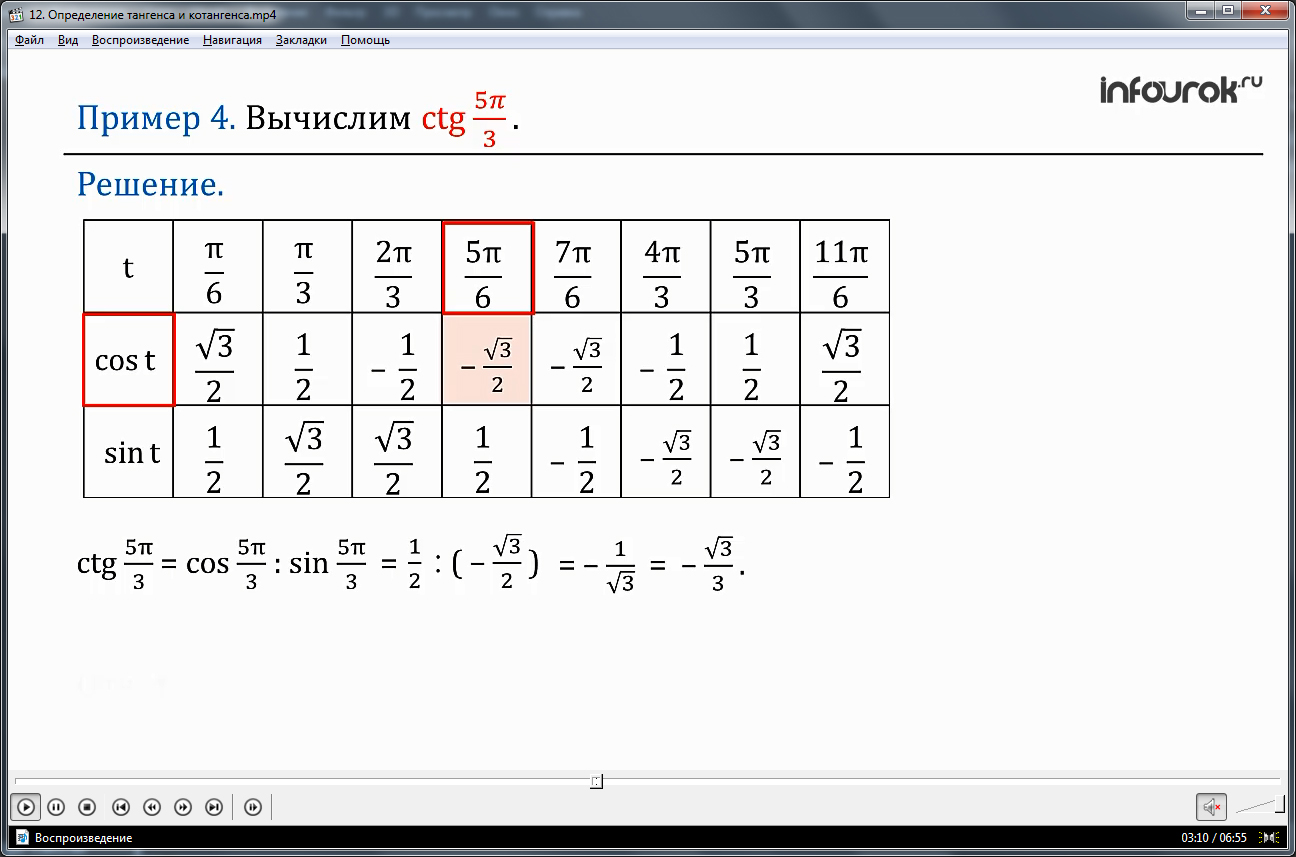
В примере 4 необходимо вычислить ctg 5π/3. Следуя формуле из определения котангенса, расписываем его в виде ctg 5π/3=(cos 5π/3)/(sin 5π/3). На экране представлена таблица значений синусов и косинусов. С помощью анимационных эффектов демонстрируется выбор нужных значений из таблицы. Выбранные значения подставляются в формулу, в результате чего получается ctg 5π/3=1/2:(-√3/2)=-√3/3. Это и есть найденное решение.
Отмечается, что рассмотренные примеры демонстрируют простоту нахождения значений тангенса и котангенса, используя табличные значения синусов и косинусов. Однако удобнее пользоваться таблицей, в которой отображаются основные значения тангенса и котангенса. На экране демонстрируется соответствующая таблица.
Доказываются формулы, составляющие важные равенства для решения заданий, в которых присутствуют функции тангенса и котангенса. Сначала представляются равенства tg(-t)=- tg t и ctg(-t)= -ctg t. Чтобы доказать данные равенства, используется определение тангенса и котангенса. Вместо этих функций в равенства подставляются соответствующие им формулы tg(-t)=sin(-t)/cos(-t). Зная свойства синусов и косинусов, открываем скобки sin(-t)/cos(-t)=-sin t/cos t. Эта формула соответствует значению -tg t. Таким образом, равенство tg(-t)=- tg t доказано. Аналогично доказывается справедливость второго равенства. Подставляем формулу из определения котангенса ctg(-t)= cos(-t)/sin(-t). Используя свойства синусов и косинусов, раскрываем скобки cos(-t)/sin(-t)= cos t/-sin t. Эта формула соответствует -ctg t. Второе равенство доказано.
Следующие равенства представляют свойства тангенса и котангенса от t+π. Отмечается, что для всякого допустимого t верны равенства tg(t+π)=tg t и ctg(t+π)=ctg t. Чтобы доказать утверждения, необходимо вспомнить формулы для косинуса и синуса t+π. Используем определение тангенса tg(t+π)= sin(t+π)/cos(t+π). Раскрываем скобки в выражениях с синусом и косинусом, получая -sin t/-cos t. Это формула тангенса, поэтому получаем tg(t+π)=tg t. Аналогично доказываем справедливость второго равенства. Из определения котангенса выводим ctg(t+π)= cos(t+π)/sin(t+π). Раскрываем скобки в выражениях с синусом и косинусом cos(t+π)/sin(t+π)= -cos t/-sin t. А это и есть формула котангенса. Таким образом, доказано, что ctg(t+π)=ctg t.
Затем представляются рассмотренные равенства в общем виде tg(t+πk)=tg t и ctg(t+πk)=ctg t для любого целого k. Равенство выделено в рамке, рекомендуется к запоминанию. Для усвоения и закрепления изученного материала рассматриваются примеры. В примере 5 необходимо вычислить tg 9π/4. Число под знаком тангенса можно представить в виде 9π/4=2π+π/4. Пользуясь изученной формулой в общем виде, можно отметить равенство tg 9π/4= tg(2π+π/4)= tg π/4. Значение тангенса π/4 можно выбрать из таблицы. Оно равно 1. Поэтому решение выражения tg 9π/4=1.
В примере 6 описывается поиск решения выражения ctg(-7π/6). Вначале решения используется свойство котангенса от отрицательного аргумента ctg(-7π/6)=-ctg 7π/6. Выражение, заключенное под знаком котангенса, преобразуется к виду 7π/6=π+π/6. Используя еще одно свойство котангенса, изученное ранее в данном уроке, находим -ctg(π+π/6)= -ctg π/6. Соответствующее табличное значение котангенса равно -√3. Задача решена.
Видеоурок «Определение тангенса и котангенса» рекомендуется использовать на традиционном уроке математики в школе. Также его применение целесообразно в ходе дистанционного обучения. Полезен материал будет и учащимся, самостоятельно осваивающим материал, для самостоятельной работы дома.
ТЕКСТОВАЯ РАСШИФРОВКА:
Тема нашего занятия «ОПРЕДЕЛЕНИЕ ТАНГЕНСА И КОТАНГЕНСА».
Слова диктора
Дадим определение тангенса и котангенса числа.
ОПРЕДЕЛЕНИЕ. Отношение синуса числа t к косинусу этого же числа называют тангенсом числа t и обозначают tgt:
tgt = , где t ≠ + πk; kϵZ (где тэ не равно пи на два, плюс пи ка, ка принадлежит зэт)
Отношение косинуса числа t к синусу этого же числа называют котангенсом числа t и обозначают сtgt:
ctgt = , где t ≠ πk; kϵZ. ( где тэ не равно пи ка, ка принадлежит зэт)
Зная таблицу знаков синуса и косинуса по четвертям числовой окружности, составим таблицу для тангенса и котангенса:
Рассмотрим примеры.
ПРИМЕР 1. Вычислим tg (тангенс пи на три)
Решение. tg = = ׃ = .( так как по определению тангенс – это отношение синуса к косинусу, значит тангенс пи на три равно синус пи на три деленное на косинус пи на три , а так как синус пи на три равен корень из трех на два, косинус пи на три равен одной второй, получаем корень из трех на два разделить на одну вторую, равно корень из трех).
ПРИМЕР 2 Вычислим tg (тангенс пять пи на четыре)
используя таблицу 2 значений синуса и косинуса числа t найдем tg = =׃ = 1( тангенс пять пи на четыре равно синус пять пи на четыре деленное на косинус пять пи четыре , а так как синус пять пи на четыре равен минус корень из двух на два, косинус пять пи на четыре равен минус корень из двух на два, получаем минус корень из двух на два разделить на минус корень из двух на два, равно единице).
ПРИМЕР 3 Аналогично первому примеру вычислим сtg (котангенс три пи деленное на два)
сtg = = 0 ׃ (–1) =0( так как по определению котангенс – это отношение косинуса к синусу, значит котангенс три пи на два равно косинус три пи на два деленное на синус три пи на два , а так как косинус три пи на два равен нулю, синус три пи на два равен минус единице , получаем нуль).
ПРИМЕР 4 Вычислим сtg (котангенс пять пи на три)
используя таблицу 3 значений синуса и косинуса числа t
найдем значение сtg = = : = = ( котангенс пять
пи на три равно отношению косинуса пять пи на три на синус пяти пи на три, равно одной второй деленной на минус корень из трех на два, равно минус единица на корень из трех, равно минус корень из трех на три).
Из приведённых примеров видно, что значения тангенса и котангенса числа t не сложно высчитать, используя таблицу значений синуса и косинуса. Но более удобно пользоваться таблицей основных значений тангенса и котангенса.
Составим таблицу основных значений тангенса и котангенса:
Докажем важные формулы для тангенса и котангенса.
1.Для любого допустимого значения
t справедливы равенства:
tg (–t) = – tg t
ctg (–t) = – ctg t
(Тангенс от минус тэ равен минус тангенсу тэ.
Котангенс от минус тэ равен минус котангенсу тэ.)
Доказательство.
Так как для косинуса и синуса справедливо, что
cos ( – t) = cos t , sin ( –t) = – sin t, то
tg ( – t) = = = – tgt,(тангенс от минус тэ равно отношению синуса от минус тэ на косинус от минус тэ равно отношению минус синуса тэ на косинус тэ равно минус тангенсу тэ)
сtg ( - t) = ==– ctgt,(котангенс от минус тэ равно отношению косинуса от минус тэ на синус от минус тэ равно отношению косинуса тэ на минус синус тэ равно минус котангенсу тэ).
2.Для любого допустимого значения
t справедливы равенства:
tg (t+π) = tgt
ctg (t+π) = ctgt
Тангенс тэ плюс пи равен тангенсу тэ, котангенс тэ плюс пи равен котангенсу тэ.
Доказательство.
Известно, что для косинуса и синуса справедливы равенства cos (t + π) = – cost , sin (t + π) = – sint.
Тогда имеем :
tg (t + π) = = = tgt,( тангенс тэ плюс пи равно отношению синуса тэ плюс пи к косинусу тэ плюс пи равно отношению минус синуса тэ к минус косинусу тэ равно тангенсу тэ)
сtg (t + π) = = = ctgt,( котангенс тэ плюс пи равно отношению косинуса тэ плюс пи к синусу тэ плюс пи равно отношению минус косинуса тэ к минус синусу тэ равно котангенсу тэ).
И вообще справедливы равенства
tg (t+πk) = tgt
ctg (t+πk) = ctgt, где ка –любое целое число и kϵZ (ка принадлежит зэт).
Рассмотрим еще один пример.
Вычислим tg (тангенс девять пи на четыре)
Решение. Так как = 2π + (девять пи на четыре равно сумме двух пи и пи на четыре), то, воспользовавшись обобщением свойства 2, получим
tg = tg (2π + ) (тангенс девять пи на четыре равен тангенсу два пи плюс пи на четыре) = tg =1. (равно тангенсу пи на четыре равно единице).
Вычислим сtg. При решении воспользуемся свойством 1 и свойством 2:
сtg = – сtg = – сtg(+) = – сtg = ( котангенс минус семь пи на шесть равно минус котангенсу семи пи на шесть равно минус котангенс пи плюс пи на шесть равно минус котангенс пи на шесть равно минус корень из трех).
Текст на экране
ОПРЕДЕЛЕНИЕ. Отношение синуса числа t к косинусу этого же числа называют тангенсом числа t и обозначают tgt:
tgt = , где t ≠ + πk; kϵZ Отношение косинуса числа t к синусу этого же числа называют котангенсом числа t и обозначают сtgt:
ctgt = , где t ≠ πk; kϵZ.
Таблица знаков тангенса и котангенса:
(на экране появляется таблица знаков таблица 1)
ПРИМЕР 1. Вычислим tg
Решение. tg = = ׃ = .
ПРИМЕР 2 Вычислим tg
Решение. tg = =׃ = 1.
ПРИМЕР 3 Аналогично первому примеру вычислим сtg
Решение. сtg = = 0 ׃ (–1) =0
ПРИМЕР 4 Вычислим сtg
Решение.
Таблица 4
Формулы для тангенса и котангенса
1.Для любого допустимого значения
t справедливы равенства:
tg (–t) = – tgt
ctg (–t) = – ctg t
Доказательство.
справедливо, что
cos ( – t) = cost , sin ( –t) = – sint, то
tg ( – t) = = = – tgt,
сtg ( - t) = ==– ctgt
2.Для любого допустимого значения
t справедливы равенства:
tg (t+π) = tgt
ctg (t+π) = ctgt
Доказательство.
справедливы равенства
cos (t + π) = – cost , sin (t + π) = – sint.
Тогда имеем:
tg (t + π) = = = tgt,
сtg (t + π) = = = ctgt,
справедливы равенства
tg (t+πk) = tgt
ctg (t+πk) = ctgt, kϵZ
Рассмотрим еще один пример.
Вычислим tg

Решение. Так как = 2π +
tg = tg (2π + ) = tg =1.
Решение.
сtg = – сtg = – сtg(+) = – сtg =
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 11439 |
| Номер материала | 835 |