
Урок "Числовая окружность"

Краткое описание документа:
Видеоуроки относятся к наиболее эффективным средствам обучения, особенно таких школьных дисциплин, как математика. Поэтому автор данного материала собрал в единое целое только полезную, важную и грамотную информацию.
Данный урок рассчитан на 11:52 минут. Практически столько же времени требуется учителю на уроке для объяснения нового материала по данной теме. Хотя главным достоинством видеоурока будет тот факт, что обучающиеся будут внимательно слушать то, о чем говорит автор, не отвлекаясь на посторонние темы и разговоры. Ведь если обучающиеся будут слушать не внимательно, то упустят важный момент урока. А если материал будет объяснять учитель сам, то его обучающиеся смогут легко отвлечь от главного своими разговорами на отвлеченные темы. И, конечно, становится понятно, какой способ будет боле рационален.
Начало урока автор посвящает повторению тех функций, с которыми обучающиеся знакомились ранее в курсе алгебры. И первыми предлагается начать изучать – тригонометрические функции. Чтобы их рассматривать и изучать требуется новая математическая модель. И этой моделью становится числовая окружность, которая, как раз, и заявлена в теме урока. Для этого вводится понятие единичной окружности, задается ее определение. Далее на рисунке автор показывает все компоненты такой окружности, и что пригодится обучающимся для дальнейшего обучения. Дугами обозначаются четверти.
Затем автор предлагает рассмотреть числовую окружность. Здесь же он делает замечание, что удобнее использовать единичную окружность. На этой окружности показано, как получается точка M, если t>0, t<0 или t=0. После этого вводится понятие самой числовой окружности.
Далее автор напоминает обучающимся, как находится длина окружности. А затем он выводит длину единичной окружности. Эти теоретические данные предлагается применить на практике. Для этого рассматривается пример, где требуется найти на окружности точку, соответствующую определенным значениям чисел. Решение примера сопровождается иллюстрацией в виде рисунка, а также необходимыми математическими записями.
Согласно условию второго примера, необходимо найти точки на числовой окружности. Здесь также все решение сопровождается комментариями, иллюстрациями и математической записью. Это способствует развитию и совершенствованию математической грамотности обучающихся. Аналогично построен и третий пример.
Далее автор отмечает те числа на окружности, которые встречаются чаще других. Здесь же он предлагает сделать два макета числовой окружности. Когда оба макета готовы, рассматривается следующий, четвертый пример, где требуется найти точку на числовой окружности, соответствующую числу 1. После этого примера формулируется утверждение, согласно которому можно найти точку M, соответствующей числу t.
Далее вводится замечание, согласно которому обучающие узнают, что числу «пи» соответствуют все числа, которые попадают в данную точку при проходе ею всю окружность. Эту информацию подкрепляет пятый пример. Его решение содержит логически правильные рассуждения и рисунки, иллюстрирующие ситуацию.
ТЕКСТОВАЯ РАСШИФРОВКА:
ЧИСЛОВАЯ ОКРУЖНОСТЬ
Ранее мы изучали функции, заданные аналитическими выражениями. И эти функции называли алгебраическими. Но в школьном курсе математики изучаются функции и других классов, не алгебраические. Начнем изучение тригонометрических функций.
Для того, чтобы ввести тригонометрические функции нам понадобится новая математическая модель – числовая окружность. Рассмотрим единичную окружность. Окружность, радиус которой равен масштабному отрезку, без указания конкретных единиц измерения, будем называть единичной. Радиус такой окружности считать равным 1.
Будем пользоваться единичной окружностью, в которой проведены горизонтальный и вертикальный диаметры СА и DВ( цэ а и дэ бэ).( смотри рисунок1 ).
Дугу АВ будем называть первой четвертью, дугу ВС – второй четвертью, дугу СD – третьей четвертью, а дугу DА – четвертой четвертью.
Рассмотрим числовую окружность. Вообще, любую окружность можно рассматривать как числовую, но удобнее для этой цели пользоваться единичной окружностью.
ОПРЕДЕЛЕНИЕ Дана единичная окружность, на ней отмечена начальная точка А – правый конец горизонтального диаметра. Поставим в соответствие каждому действительному числу t (тэ) точку окружности по следующему правилу:
1) Если t>0(тэ больше нуля), то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь АМ (а эм) длины t. Точка М и будет искомой точкой М(t) (эм от тэ).
2) Если t<0(тэ меньше нуля), то, двигаясь из точки А в направлении по часовой стрелке (отрицательное направление обхода окружности), опишем по окружности путь АМ (а эм) длины |t| (модуль тэ). Точка М и будет искомой точкой М(t) (эм от тэ).
3) Числу t = 0 поставим в соответствие точку А.
Единичную окружность с установленным соответствием (между действительными числами и точками окружности) будем называть числовой окружностью.
Известно, что длина окружности L (эль) вычисляется по формуле L =2πR (эль равно два пи эр), где π≈3,14 , R – радиус окружности. Для единичной окружности R=1см, значит L =2π≈6,28 см (эль равно два пи примерно 6,28).
Рассмотрим примеры.
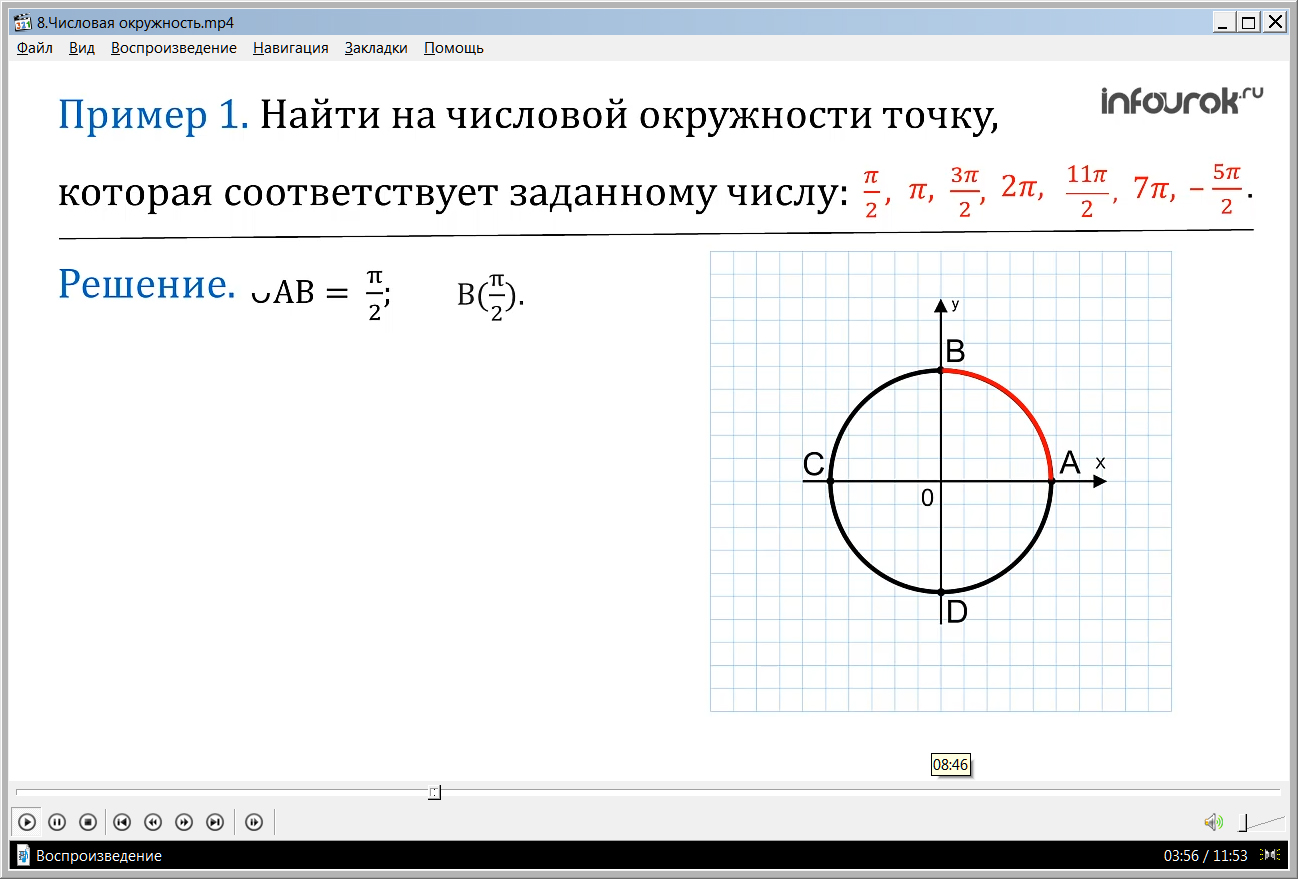
ПРИМЕР 1.Найти на числовой окружности точку, которая соответствует заданному числу: , , , , , ,.(пи на два, пи, три пи на два, два пи, одиннадцать пи на два, семь пи, минус пять пи на два)
Решение. Первые шесть чисел положительны, поэтому для отыскания соответствующих им точек окружности нужно пройти по окружности путь заданной длины, двигаясь из точки А в положительном направлении. Длина каждой четверти единичной окружности равна . Значит, АВ =, то есть числу соответствует точка В ( смотри рис. 1). АС = , то есть числу соответствует точка С. АD = , то есть числу соответствует точка D. А числу соответствует снова точка А, потому что пройдя по окружности путь длиной мы попали в начальную точку А.
Рассмотрим, где будет находится точка такое Так как мы уже знаем, что длинна окружности , то приведем к виду ( четыре пи плюс три пи на два). То есть, двигаясь из точки А в положительном направлении, нужно описать два раза целую окружность (путь длиной 4π) и дополнительно путь длиной , который закончится в точке D.
Что такое ? Это 3∙2π + π (три умноженное на два пи плюс пи). Значит, двигаясь из точки А в положительном направлении, нужно описать три раза целую окружность и дополнительно путь длиной π, который закончится в точке С.
Чтобы найти на числовой окружности точку, соответствующую отрицательному числу , нужно из точки А пройти по окружности в отрицательном направлении (по часовой стрелке) путь длиной , а это соответствует 2π + . Этот путь завершится в точке D.
ПРИМЕР 2. Найти на числовой окружности точки , , (пи на шесть, пи на четыре, пи на три).
Решение. Разделив дугу АВ пополам, мы получим точку Е, которая соответствует . А разделив дугу АВ на три равные части точками F и О, получим, что точка F соответствует , а точка T соответствует
(смотри рис 2).
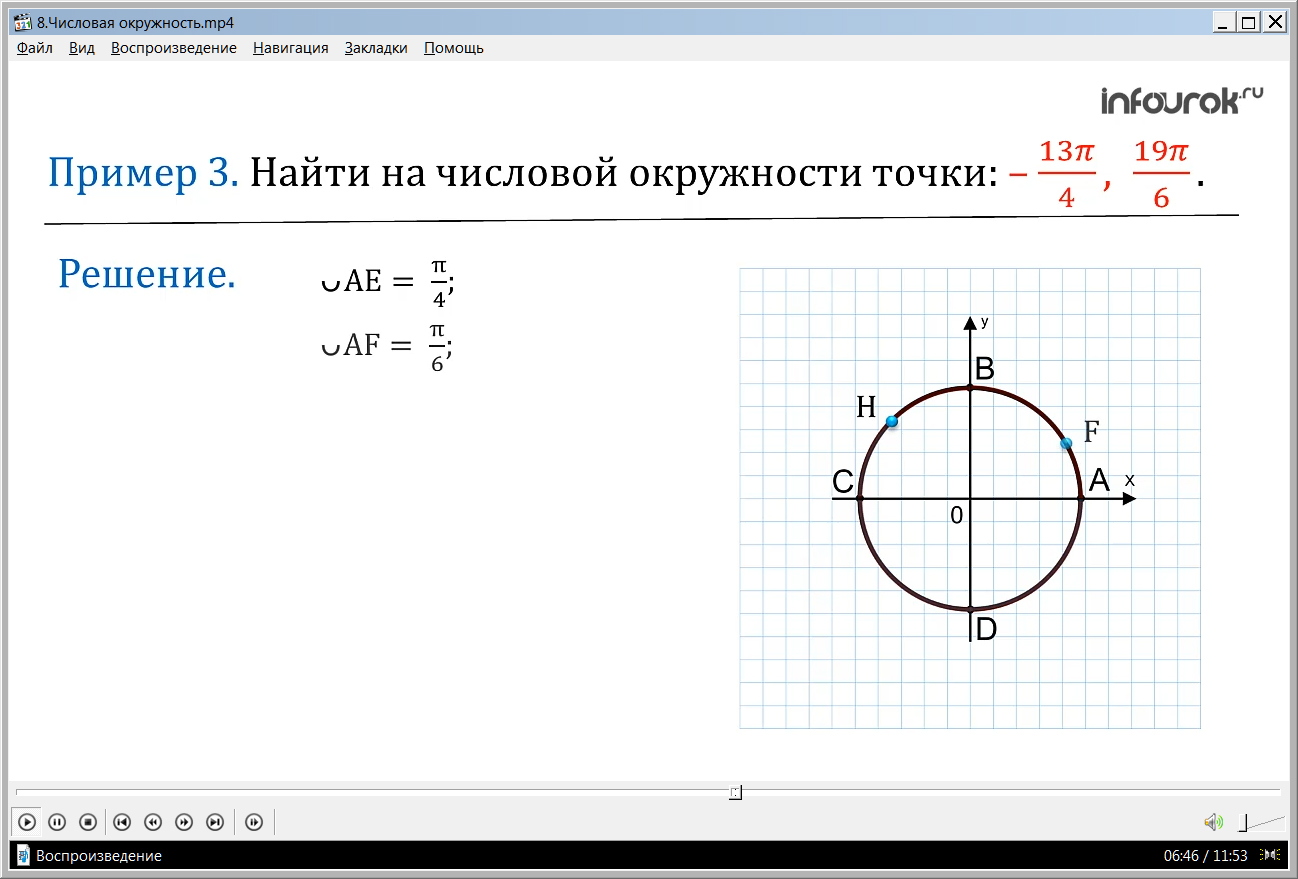
ПРИМЕР 3. Найти на числовой окружности точки , (минус тринадцать пи на четыре, девятнадцать пи на шесть).
Решение. Отложив дугу АЕ (а эм) длиной (пи на четыре) от точки А тринадцать раз в отрицательном направлении, получим точку Н (аш) – середину дуги ВС.
Отложив дугу АF длиной (пи на шесть) от точки А девятнадцать раз в положительном направлении, попадем в точку N (эн), которая принадлежит третьей четверти (дуге СD) и СN равно третьей части дуги СD (сэ дэ).
(смотри рис примера 2).
Чаще всего приходится искать на числовой окружности точки, которые соответствуют числам , , , ( пи на шесть, пи на четыре, пи на три, пи на два), а также те, которые кратны им, то есть , , , (семь пи на шесть, пять пи на четыре, четыре пи на три, одиннадцать пи на два). Поэтому для того, чтобы быстро ориентироваться целесообразно сделать два макета числовой окружности.
На первом макете каждая из четвертей числовой окружности будет разделена на две равные части и около каждой из полученных точек запишем их «имена»:
На втором макете каждая из четвертей разделена на три равные части и около каждой из полученных двенадцати точек то же запишем их «имена»:
Если двигаться по часовой стрелке, то получим для имеющихся на чертежах точек те же «имена», только со значением минус. Для первого макета:
Аналогично, если двигаться по второму макету по часовой стрелке из точки О.
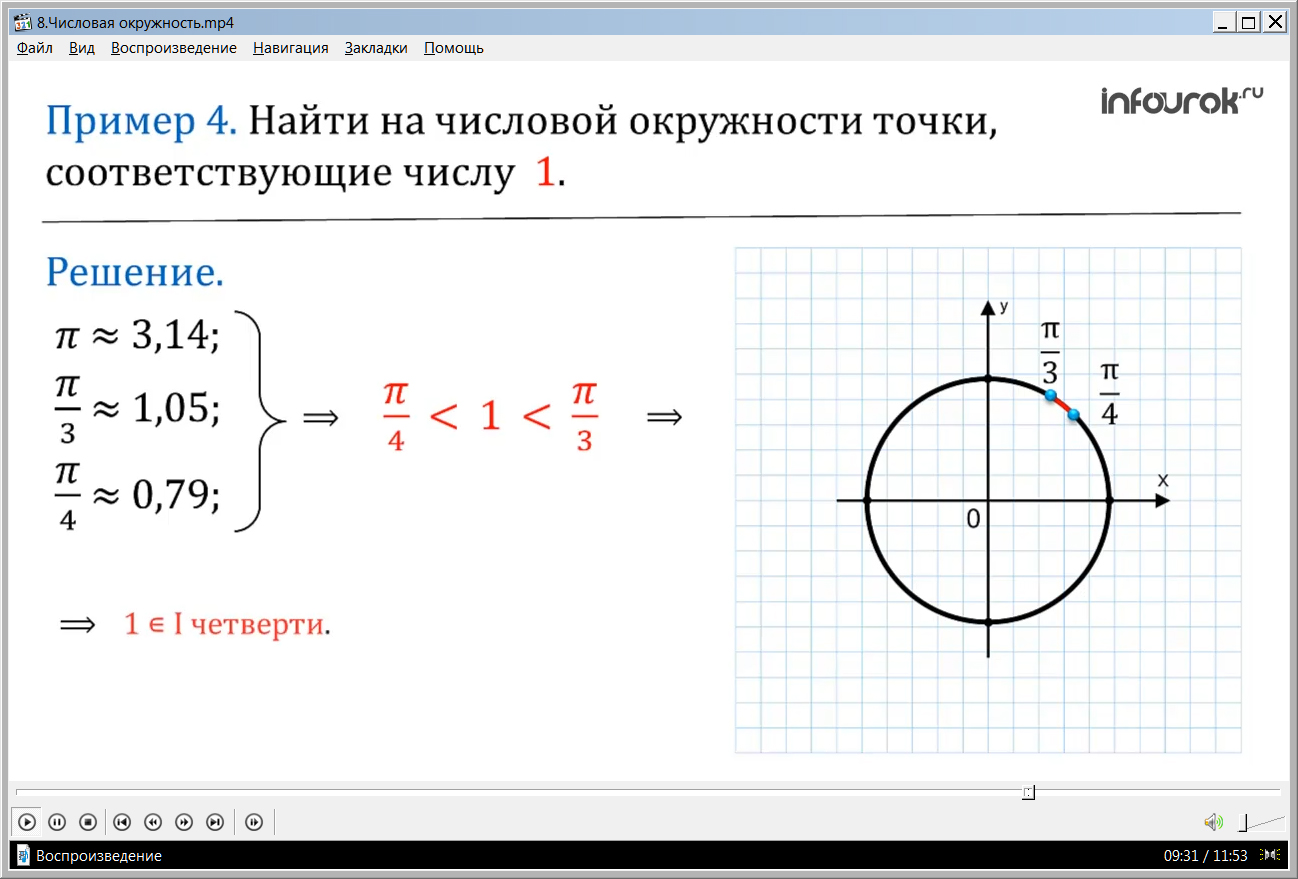
ПРИМЕР 4. Найти на числовой окружности точки, соответствующие числам 1 (один).
Решение. Зная, что π≈3,14 (пи приблизительно равно три целые четырнадцать сотых) , ≈ 1,05( пи на три приблизительно равно одна целая пять сотых), ≈ 0,79( пи на четыре приблизительно равно ноль целых семьдесят девять сотых). Значит, < 1 < ( один больше, чем пи на четыре, но меньше, чем пи на три), то есть число 1 находится в первой четверти.
Справедливо следующее утверждение: если точка М числовой окружности соответствуют числу t, то она соответствует и любому числу вида t + 2πk (тэ плюс два пи ка), где ка – любое целое число и kϵZ (ка принадлежит зэт).
Используя это утверждение, можно сделать вывод, что точке соответствуют все точки вида t =+ 2πk (тэ равно пи на три плюс два пи ка), где kϵZ(ка принадлежит зэт), а точке (пять пи на четыре) – точки вида t = + 2πk (тэ равно пять пи на четыре плюс два пи ка), где kϵZ(ка принадлежит зэт) и так далее.
ПРИМЕР 5.Найти на числовой окружности точку : а) ; б) .
Решение. а) Имеем: = =(6 + ) ∙ π = 6π + = + 3∙ 2π.( двадцать пи на три равно двадцать на три пи равно шесть плюс две трети, умноженное на пи равно шесть пи плюс два пи на три равно два пи на три плюс три умноженное на два пи).
Это значит, что числу соответствует на числовой окружности та же точка, что и числу (это вторая четверть) ( смотри второй макет на рис 4).
б) Имеем: = – ( 8 + ) ∙ π = + 2π ∙ ( – 4).( минус тридцать пять пи на четыре равно минус восемь плюс три четвертые, умноженное на пи равно минус три пи на четыре плюс два пи, умноженное на минус четыре). То есть числу соответствует на числовой окружности та же точка, что и числу
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 13537 |
| Номер материала | 831 |