
Урок "Иррациональные уравнения". Часть 2

Краткое описание документа:
Итак, мы познакомились с понятием иррационального уравнения, видом и особенностями этого уравнения. Чтобы решить такое уравнение, нужно освободиться от знака квадратного корня (или знака корня более высокой степени, например, кубического корня). Как уже отмечалось, одним из методов решения (да, пожалуй, основным методом) является возведение уравнения в степень. Мы рассмотрели решение простейших иррациональных уравнений. А как решить более сложные уравнения? Существуют ли другие методы решения иррациональных уравнений? Ответы на эти вопросы ищем в видеоуроке.
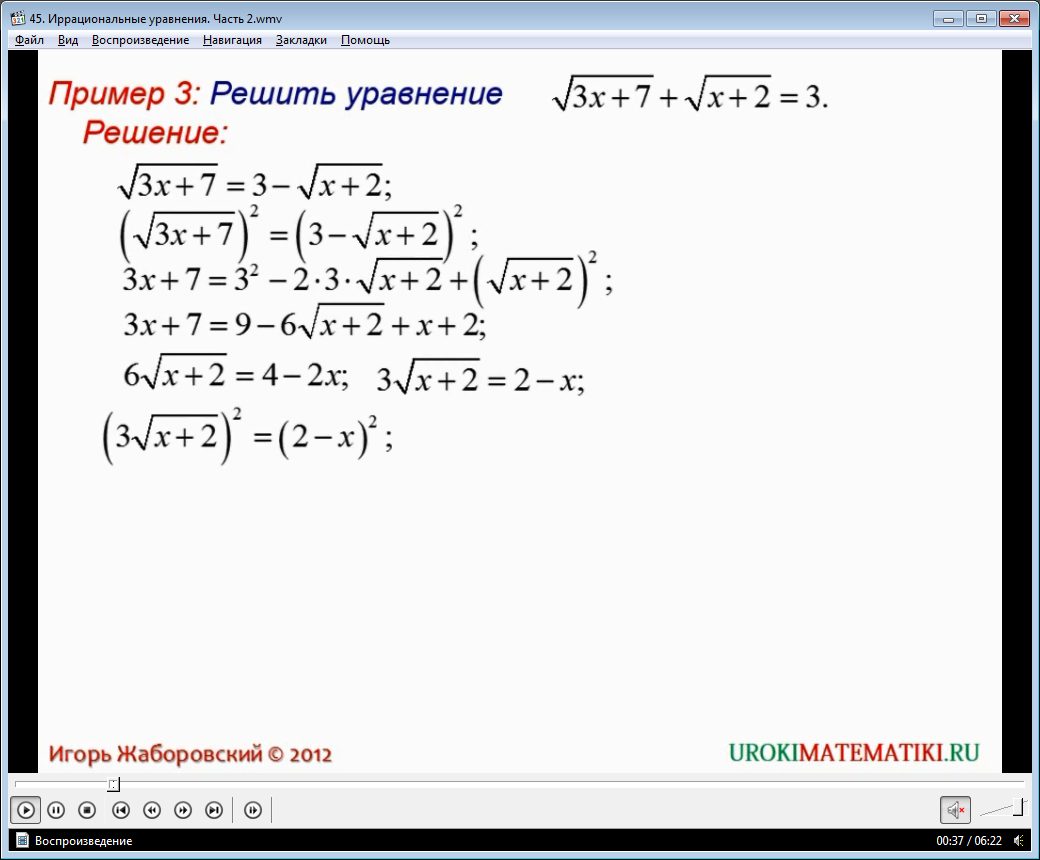
Пример 3. √(3х +7) + √(х + 2) + 3.
Здесь в левой части уравнения находятся два квадратных корня. Можно обе части данного уравнения возвести в квадрат. А можно поступить по-другому, как это показано в видеоуроке. Перенесем один из квадратных корней в правую часть. Получим:
√(3х + 7) = 3 - √(х + 2).
Теперь возводим обе части уравнения в квадрат и получим такое выражение:
3х + 7 = 32 – 2 * 3 * √(х + 2) + (√(х + 2))2.
Такой перенос одного из корней в правую (или в левую) часть уравнения в случае более сложных подкоренных выражений поможет существенно облегчить решение.
Смотрим видеоурок дальше. В результате преобразований получаем выражение:
3√(х + 2) = 2 – х.
Теперь чтобы найти решение, нужно еще раз применить метод возведения в квадрат.
Дальнейшие преобразования подробно показаны в видеоуроке. Мы нашли два корня:
х1 = 14 и х2 = -1.
Обязательной частью решения иррациональных уравнений является проверка. Ведь в результате преобразований у нас могут появиться посторонние корни. В нашем видеоуроке показано, что посторонним корнем является х1 = 14, а х2 = –1 – корень исходного уравнения.
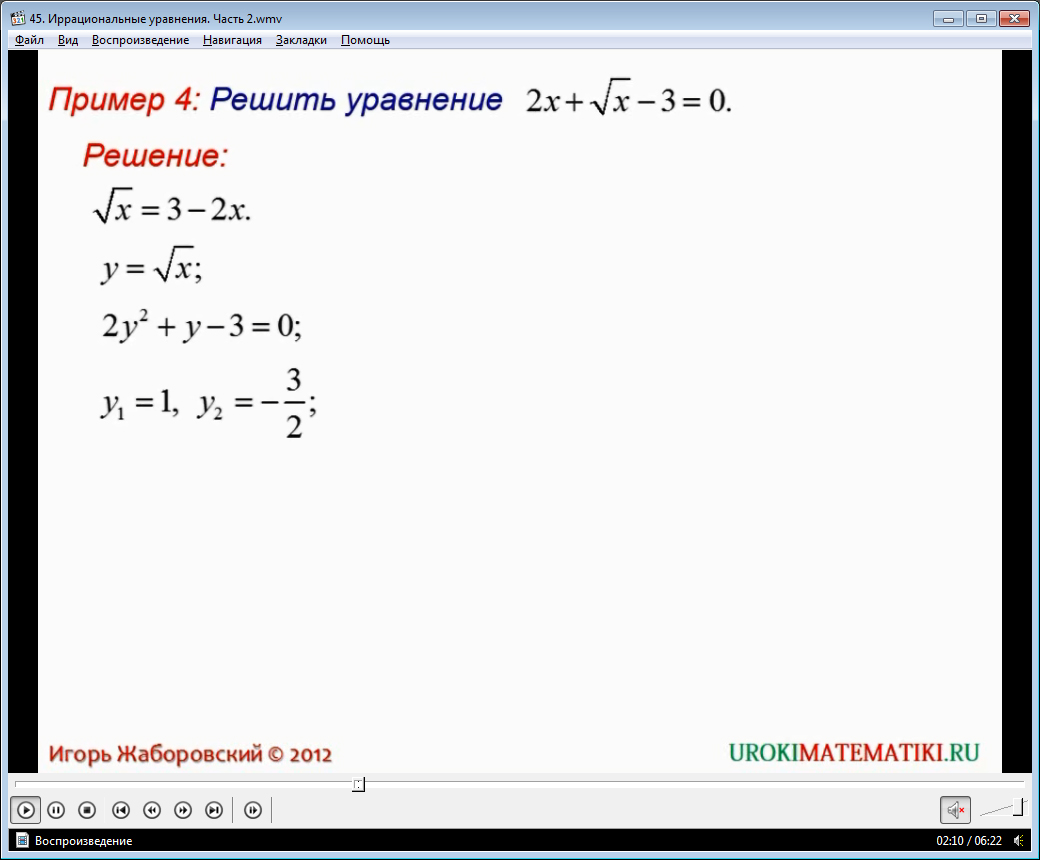
Пример 4. 2х + √х – 3 = 0.
Сейчас видеоурок познакомит нас с еще одним очень удобным способом решения иррациональных уравнений. Это метод введения новых переменных.
Обозначим у = √х. Тогда получается квадратное уравнение относительно новой переменной у:
2у2 + у – 3 = 0.
В результате решения полученного уравнения получается два корня: у1 = 1 и у2 = – 3/2.
Возвращаемся к замене и видим, что задача свелась к решению двух уравнений: √х = 1 и √х = -3/2. Второе уравнение не имеет корней, а из первого получаем х = 1.
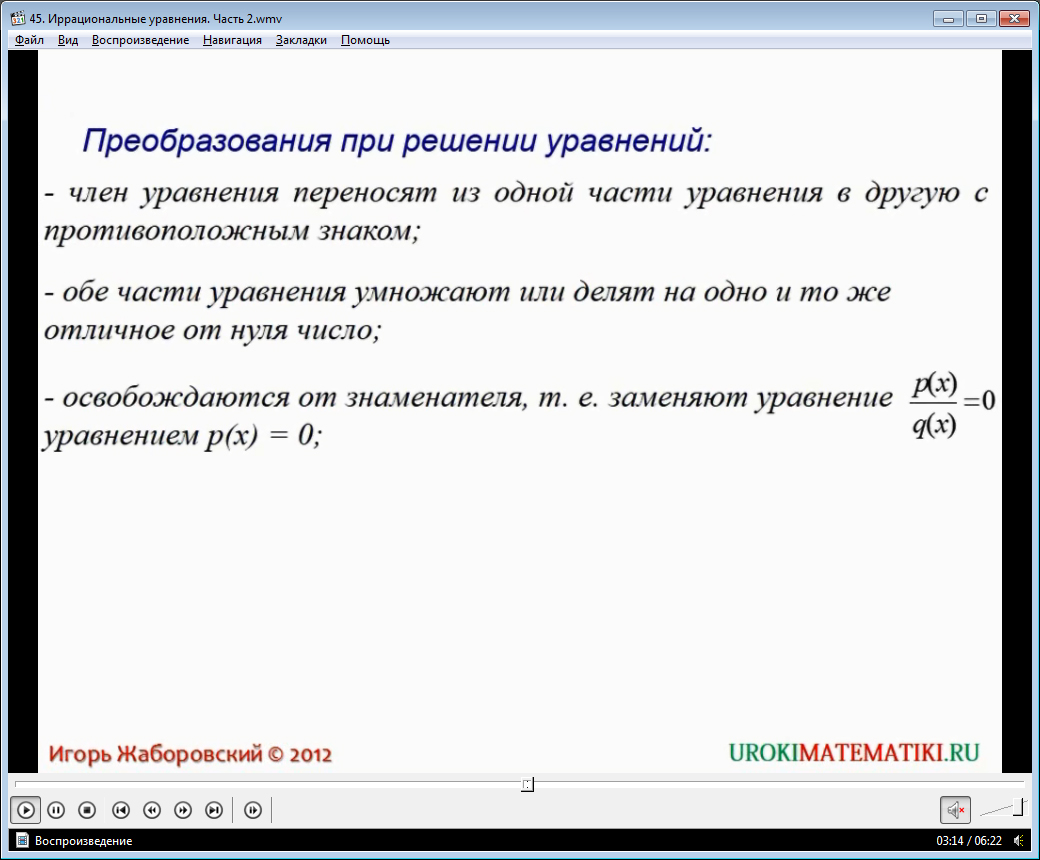
При решении различных уравнений, будь то линейные, квадратные, рациональные или иррациональные уравнения, выполняются различные преобразования: перенос какого-либо члена уравнения из одной части в другую с противоположным знаком; умножение или деление обеих частей уравнения на одно и то же отличное от нуля число и т. д.
В результате некоторых преобразований могут появиться посторонние корни, поэтому нужно проверять все найденные корни. Чтобы осмыслить все это с теоретической точки зрения, смотрим видеоурок.
Замены данного уравнения более простым, но равносильным ему, называют равносильным преобразованием уравнения.
Два уравнения f(x) = g(x) и r(x) = s(х) называют равносильными, если они имеют одинаковые корни. Заметим, что если оба уравнения не имеют решений, то они также являются равносильными.
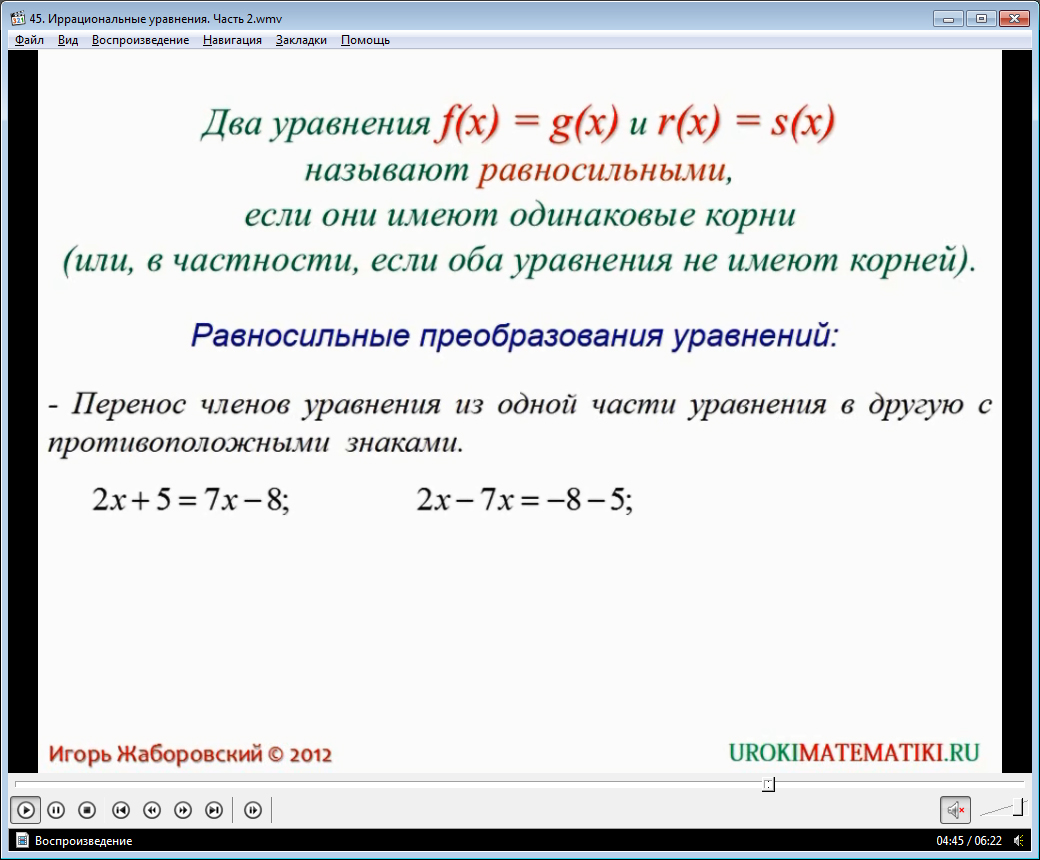
Подробно о равносильных преобразованиях рассказывается в видеоуроке.
Равносильными преобразованиями уравнения являются следующие:
1. Перенос членов уравнения из одной части уравнения в другую с противоположными знаками.
2. Умножение или деление обеих частей уравнения на одно и то же отличное от нуля число.
А вот такие преобразования уравнений как:
1. Освобождение от знаменателей, содержащих переменные;
2. Возведение обеих частей уравнения в квадрат.
являются неравносильными. Почему? Ответ найдете в видеоуроке.
Однако при решении уравнения приходится применять неравносильные преобразования. Поэтому все найденные корни надо проверить подстановкой в исходное уравнение, чтобы исключить посторонние корни.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5696 |
| Номер материала | 567 |