
Урок "Рациональные уравнения как математические модели реальных ситуаций" часть 4

Краткое описание документа:
Видеоурок на тему «Рациональные уравнения как математическая модель реалистичных ситуаций» будет полезен восьмиклассникам при изучении одной из важных уроков из области изучении рациональных выражений. О том, что такое множество рациональных чисел, как выглядит рациональное число, и чем оно отличается от других, было изучено в предыдущих классах. С этими понятиями школьники будут периодически сталкиваться на разных классах и изучать более детально в зависимости от конкретного применения.
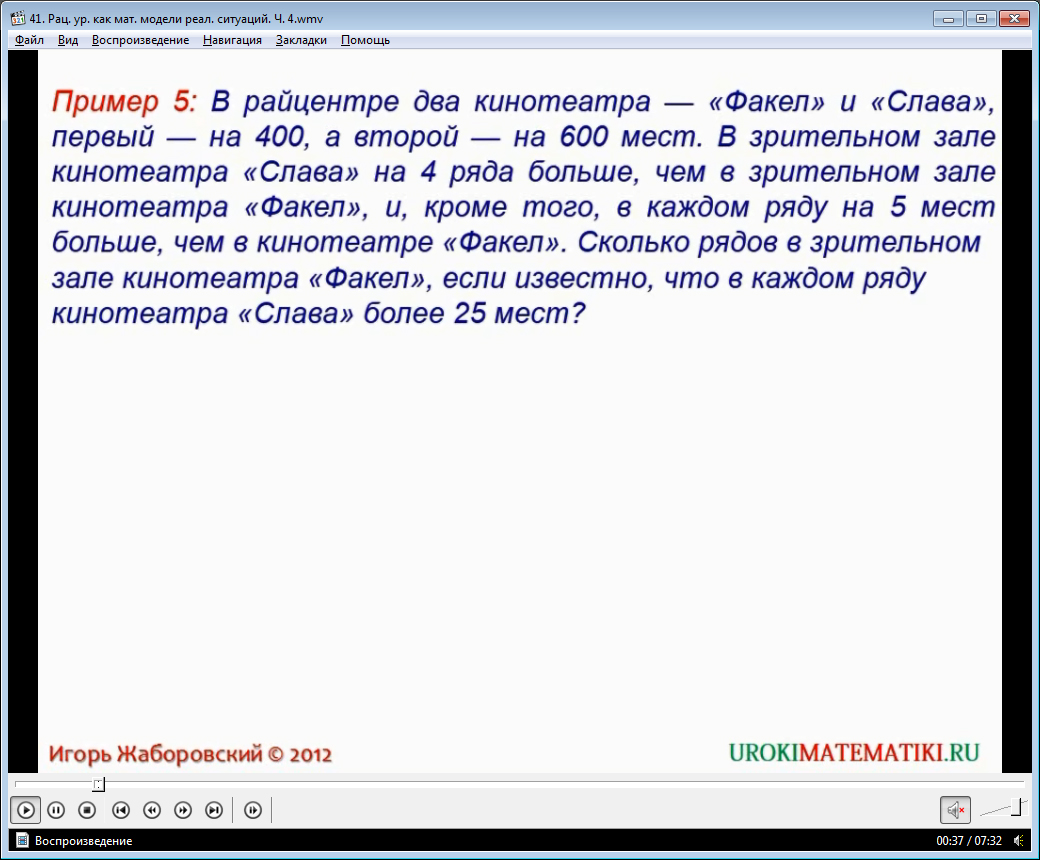
Данная же тема касается рациональным выражениям и уравнениям. В результате создания модели тех или иных задач могут возникнуть уравнения с рациональными корнями или в целом рациональные уравнения. Школьники должны уметь с ними справляться, иначе задачи они не решат.
Где могут появиться такие задачи на практике? Этому и посвящен данных обучающий ресурс.
Смотреть видеоурок можно только в комплексе с предыдущими, в противном случае, он не будет иметь никакого смысла, ведь является логическим продолжением трех предыдущих.
Начинается электронный обучающий ресурс с задачи. Диктор ее зачитывает вслух. Она также выводится на экран понятным текстом, с читабельным шрифтом и выбранными цветами. Размер текста адаптирован под критерии для максимального удобства пользованием материала во время уроков либо при индивидуальном просмотре.
Решение задачи приводится сразу после того, как условие подробное проговаривается. Ученики в тетрадях могут выполнить сокращенное описание задачи, чтобы оно, во-первых, лучше запомнилось, во-вторых, было перед глазами во время просмотра решения.
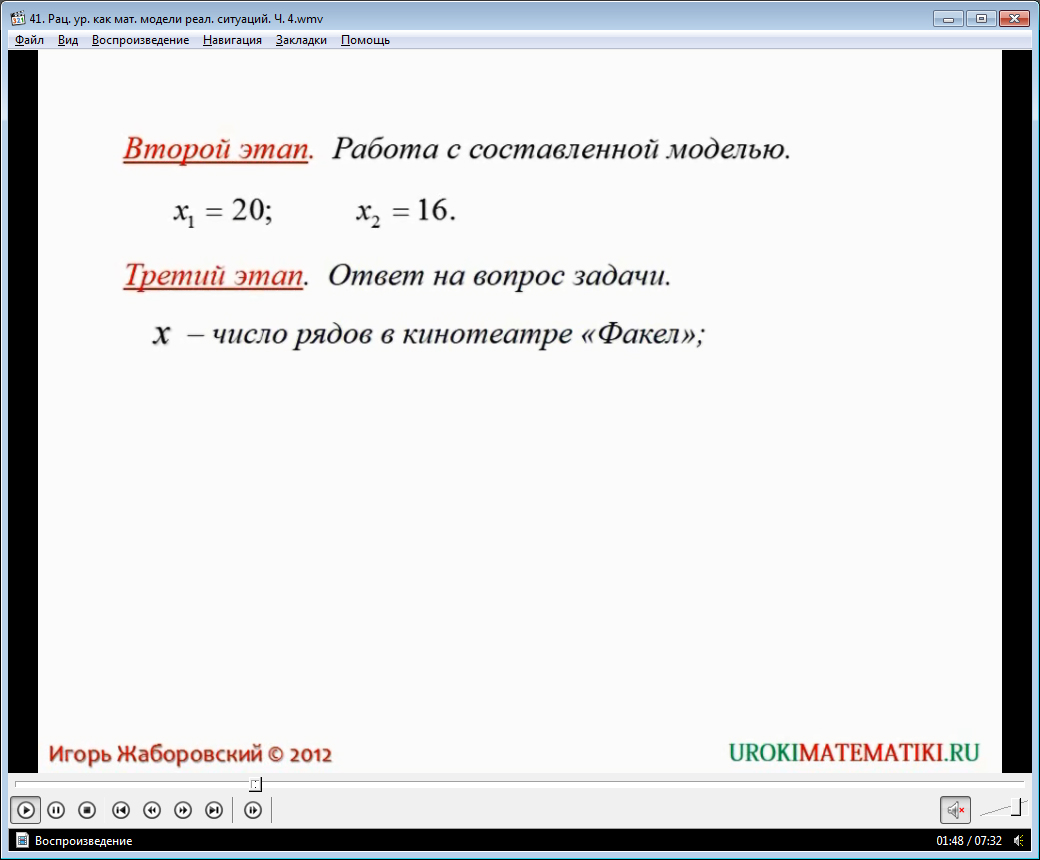
Решение выводится поэтапно. На первом этапе производится замена неизвестных через х. Исходя из тех или иных данных в задаче, некоторые параметры могут записываться в виде операций с указанным х.
В результате имеем математическую модель. Об этом говорит диктор. Что представляет собой математическая модель данной задачи? Разумеется, рациональное уравнение. Уровень сложности не такое высокое. Школьники со средней подготовке в восьмом классе должны уметь справляться с таковыми. Прежде, чем продемонстрировать им следующие этапы решения, можно предоставить им возможность решить самостоятельно и найти корни рационального уравнение, либо доказать, что оно не имеет решения, что также не исключено.
На втором этапе выводятся два найденных корня уравнения. На третьем же этапе – на экране выводится ответ задачи.
Как видим, решение данной задачи не составляет никакой сложности. Важно просмотреть каждый момент подробно и тщательно. Не стоит переходить к рассматриванию следующего этапа решения задачи, если предыдущий непонятен.
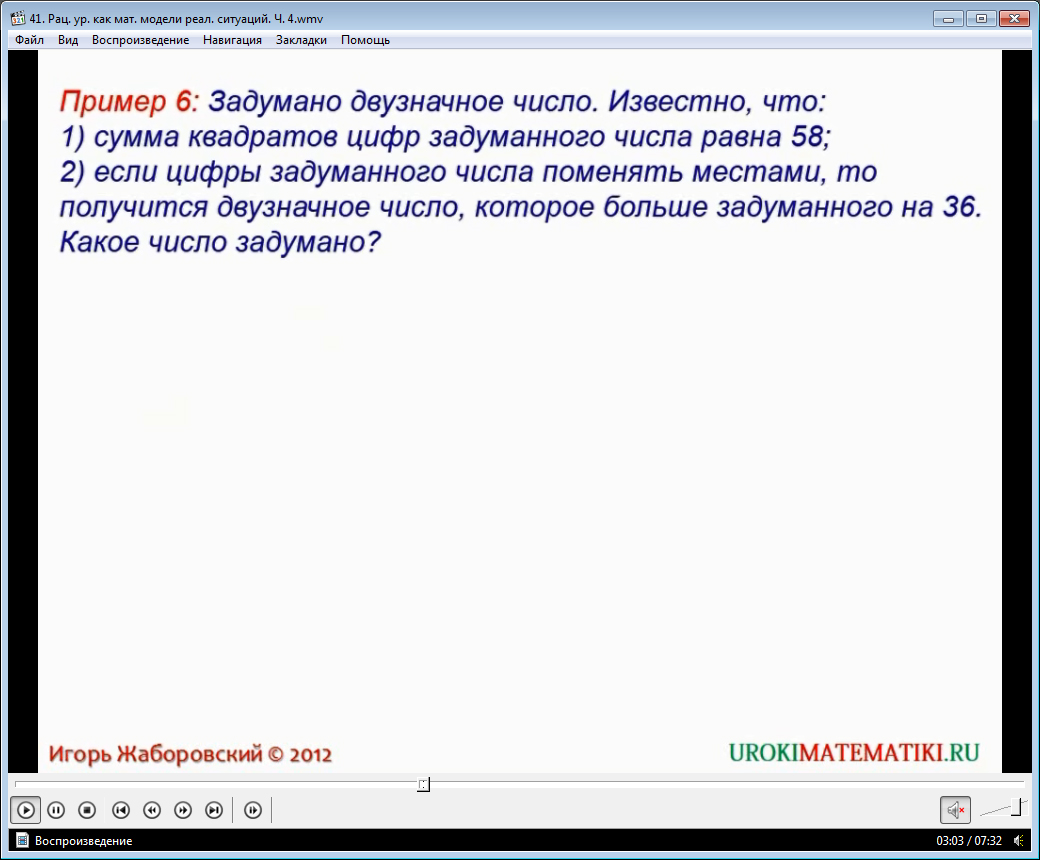
Далее приводится условие еще одной задачи. Она достаточно интересна, чтобы привлечь внимание школьников. Необходимо найти некоторое двухзначное число, если известны некоторые данные о нем. Условие задачи диктор читает вслух.
Решается задача аналогичным образом. То есть, на первом этапе составляется математическая модель, в данном случае, она представляет собой систему рациональных уравнений, на втором этапе выводятся корни данного уравнения, и на третьем этапе из этих корней подбираются удовлетворяющие условию задачи значения. Далее выводится на экран ответ.
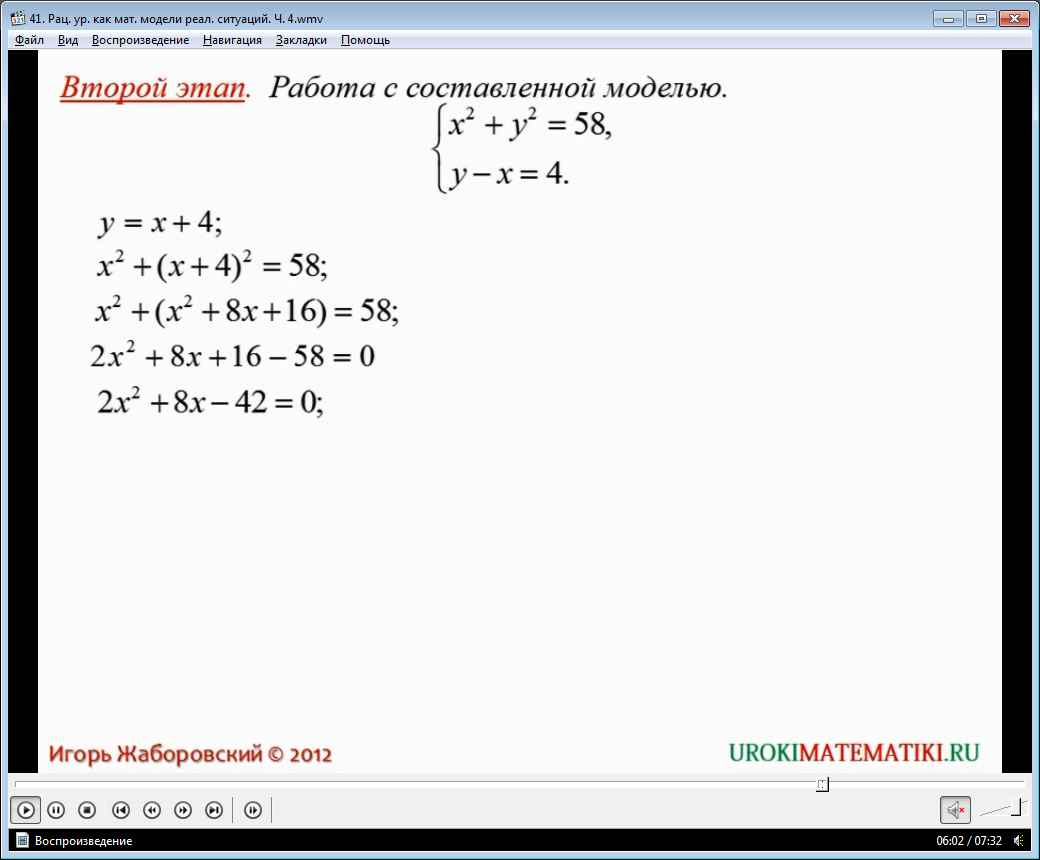
Если хорошо понять материал, изложенный в данном видеоуроке, можно с легкостью справляться с практическими задачами. С помощью данного и предыдущих ресурсов, можно подготовиться самостоятельно к предстоящим контрольным работам. Также материал будет полезен при выполнении домашних работ либо написания плана-конспекта для учителей.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 3590 |
| Номер материала | 563 |