
Урок "Теорема Виета"

Краткое описание документа:
Решению квадратных уравнений посвящено огромное количество учебных материалов. Решать их можно как графическим методом, так и аналитическим. Выбор метода решения подобных уравнений зависит от некоторых факторов. Главное, не ошибиться с выбором и не усложнять себе задачу.
Ранее восьмиклассники сталкивались с графическим способом решения, вернее, способами решения, ведь их огромное количество. При выборе необходимого способа, нужно опираться на конкретный пример. Некоторые уравнения можно построить непосредственно сразу, другие требуют дополнительных преобразований. В любом случае, суть данных методов в том, что они упрощают решение и делают его более наглядным.
Также школьники сталкивались с двумя формулами, которые помогают алгебраическим методом решить квадратные уравнение. Первая из них – это формула с дискриминантом, вторая – иная формула для частных случаев. Последняя является неким следствием из первой.
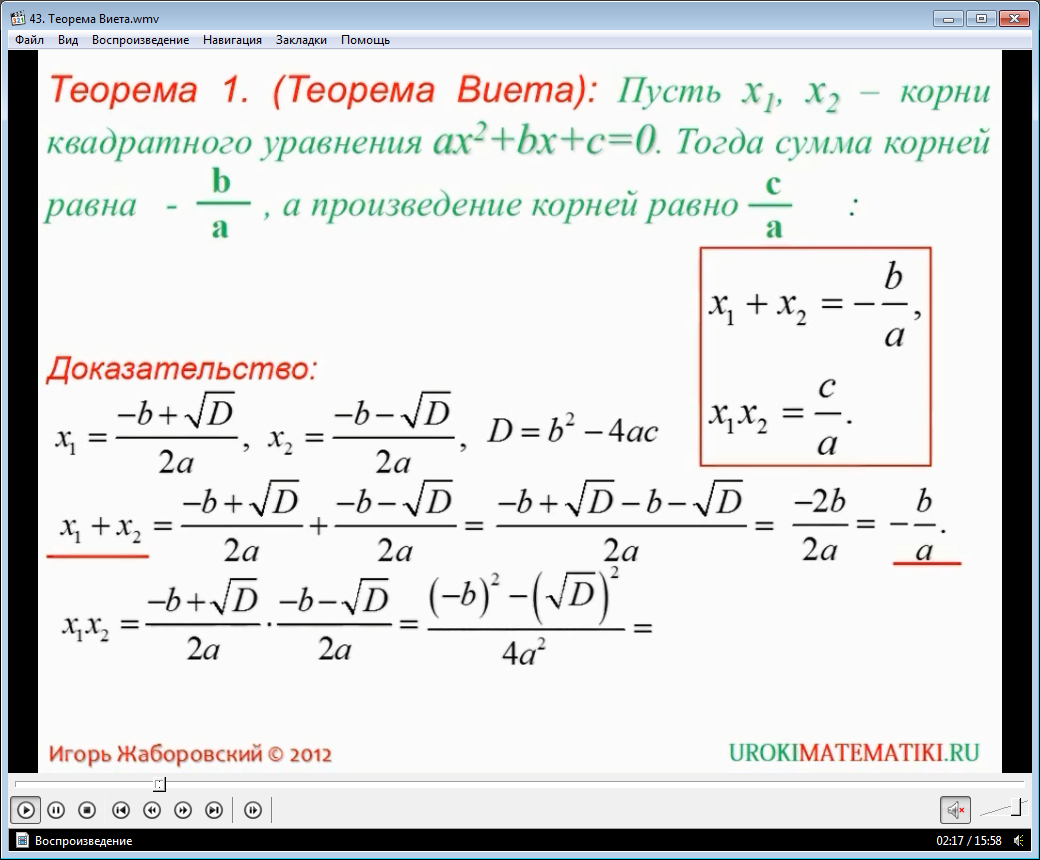
Данный видеоурок откроет для школьников еще один метод, который поможет в разы упростить решение определенного класса квадратных уравнение. Называется он «Теоремой Виета». О том, в чем суть теоремы, откуда она появилась и как ее применять, будет рассказано, непосредственно, в видеоуроке, который сопровождает уверенным и спокойным голосом диктора.
Итак, для каких случаев стоит применять теорему Виета?
На экран выводится общая формулировка теоремы. Диктор объясняет ее суть. Также с правой стороны экрана выводится сама формула, с помощью которого можно найти два корны уравнения. Общий вид квадратного уравнения, которое подойдет для решения таким методом содержится в формулировке теоремы Виета.
Сразу же, приводятся некоторые примеры, чтобы стало понятно, в чем суть теоремы. Однако еще не совсем ясно, какую практическую пользу она дает.
Дело в том, что при некоторых простых коэффициентах, можно, не решая уравнение, а лишь воспользовавшись теоремой, угадать корни. Подобный пример является вторым.
Чтобы не оставить теорему на уровне ее формулировки, в видеоуроке приводится ее доказательство. Ученики с очень низкой базой могут его пропустить. Однако при желании, они могут попробовать рассмотреть самостоятельно либо индивидуально с репетитором или учителем по алгебре.
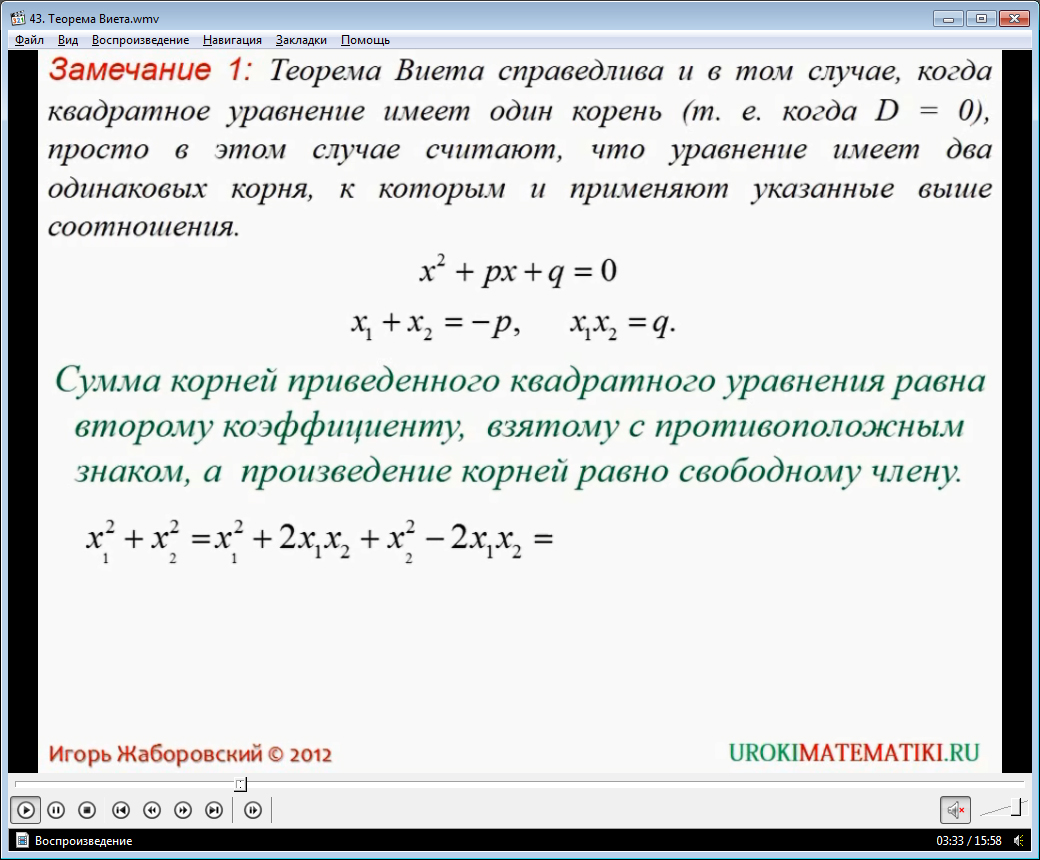
После того, как диктор подробным образом комментирует доказательство, начинается следующая часть видеоурока, в которой рассматриваются некоторые замечания. Например, первое из них касается тому, что в определенном случае, квадратное уравнение может иметь только один корень, иными словами оба корня повторяются.
Далее приводится еще одна теорема, которая в дальнейшем достаточно часто будет выручать школьников при решении различных квадратных уравнений.
Теорема гласит о том, что любое квадратное уравнение любой сложности можно представить в виде множителей. Формула приведение в такой вид выводится на экран. Как видим, для того, чтобы ею воспользоваться, необходимо предварительно найти корни того или иного уравнения. Таким образом, если квадратное уравнение не имеет решений, данная теорема не будет иметь смысла.
Еще одна теорема приводится для рассмотрения. Она гласит о том, что если принцип предыдущей теоремы работает, то квадратное уравнение однозначно имеет корни, то есть решение.
Приводится доказательство. Все теоремы подкрепляются практическими примерами и уравнениями в общем виде.
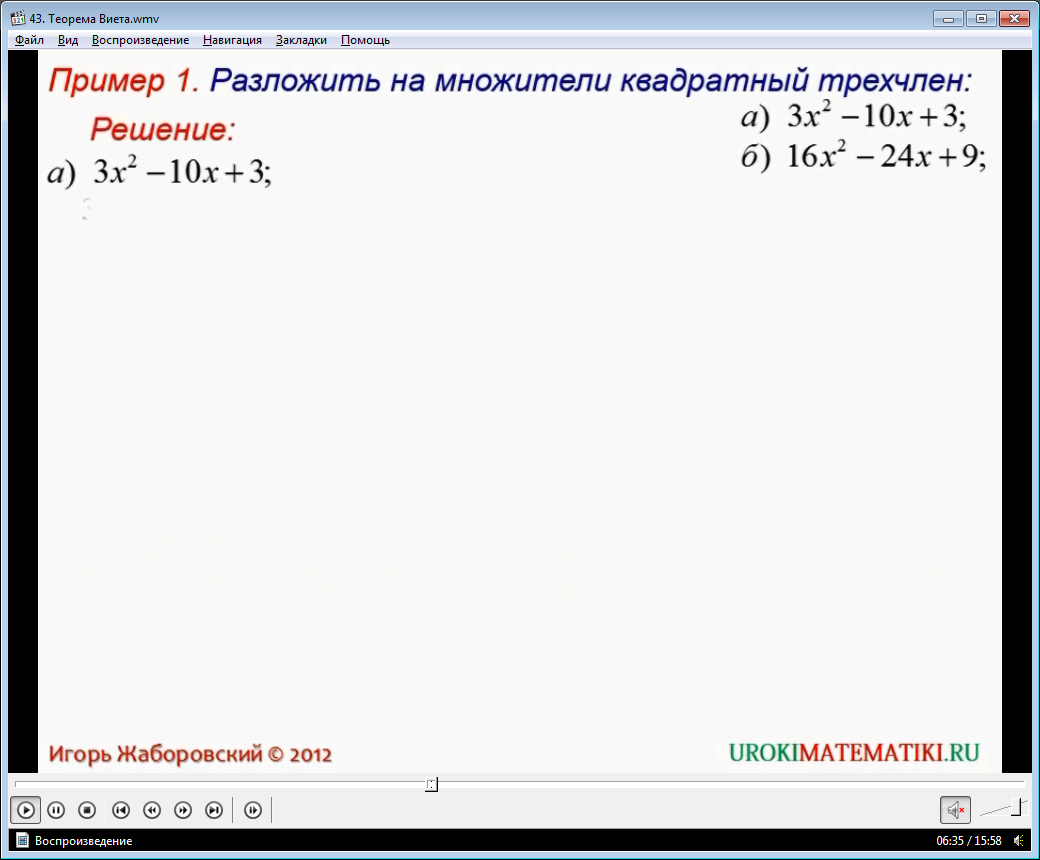
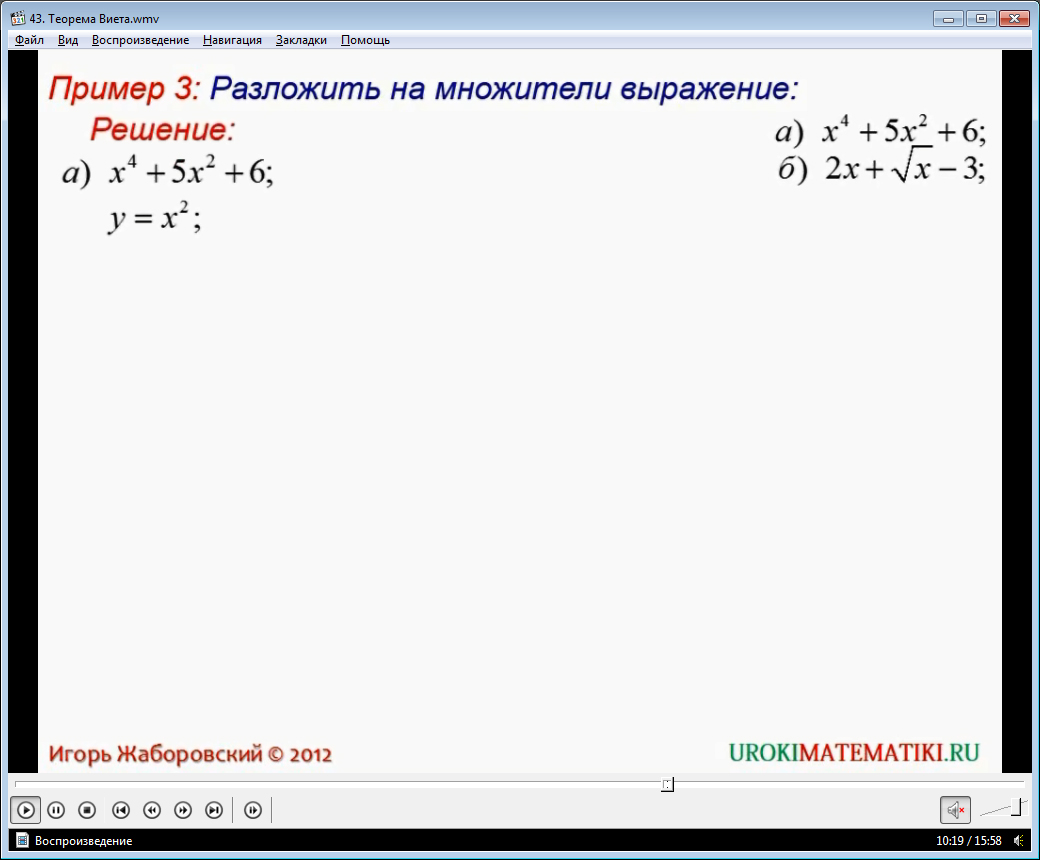
Далее в видеоуроке начинается практическая часть. Примеры, которые рассматриваются, можно задать в качестве домашнего задания, либо просто рассмотреть в классе. При их полном разборе, школьники смогут в дальнейшем самостоятельно справляться с аналогичными примерами.
Видеоурок придаст обычному школьному уроку интересный и увлекательный оттенок. С помощью него, можно рассмотреть теорему Виета в классе, заинтересовать учеников и провести намного эффективнее урок.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7557 |
| Номер материала | 565 |