
Урок "Ещё одна формула корней квадратного уравнения"

Краткое описание документа:
Квадратные уравнение представляют собой отдельный раздел, который охватывает большое количество уроков в восьмом классе в курсе изучения алгебры. Темы достаточно интересны для тех, кому по душе справляться с различными алгебраическими примерами и для тех, кто любит математическую практику.
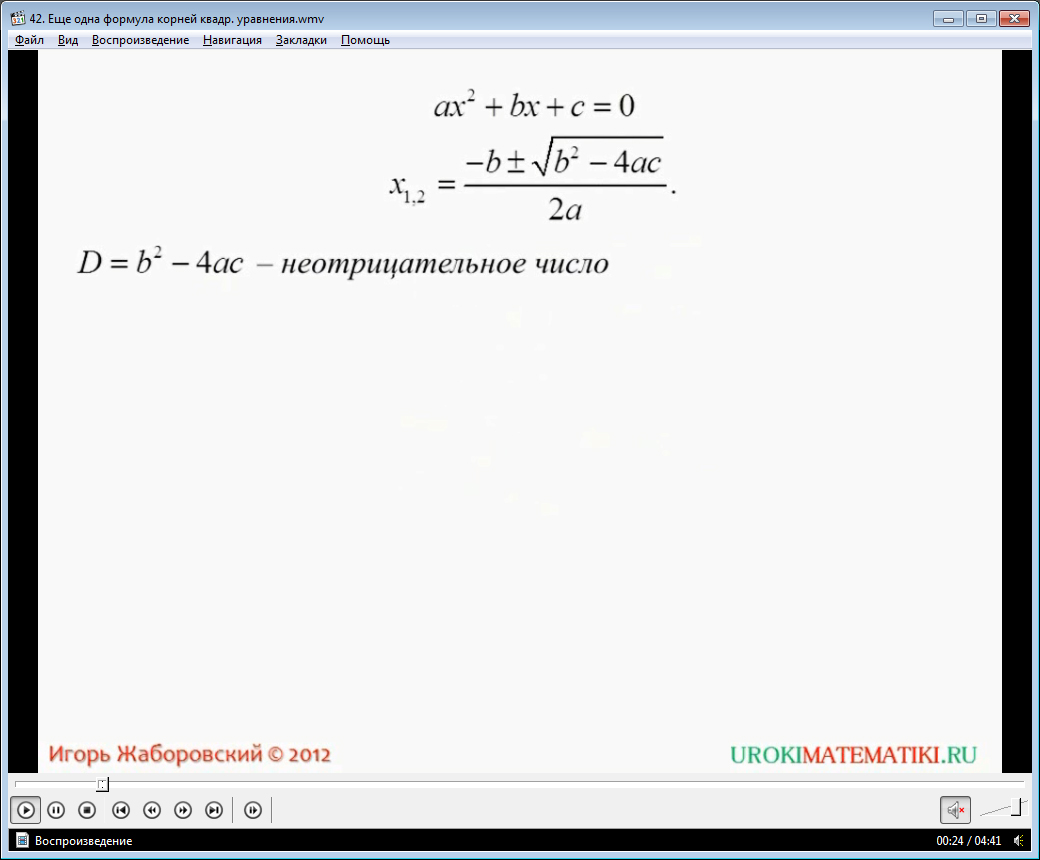
При решении практически любых квадратных уравнений, необходимо в первую очередь определить, какие конкретно методы и алгоритмы подойдут. Оценка сложности и вида квадратного уравнения является важным процессом. В противном случае, можно усложнить себе задачу. Иногда квадратные уравнения очень просто можно решить с помощью графического изображения. Графических способов решения достаточно много. Главное, правильно подобрать именно тот способ, который будет являться наиболее оптимальным для конкретного случая.
Однако существует также большое количество алгебраических методов. Один из данных методов будет рассматриваться в видеоуроке «Еще одна формула корней квадратного уравнения».
Вначале видеоурока диктор напоминает школьникам простую формулу, с помощью которой они ранее решали алгебраическим методом квадратные уравнения. Речь идет о формуле, в которой используется дискриминант. Стоит также вспомнить, что если найденный дискриминант отрицателен, то уравнение не имеет корней. Если он равен нулю – то решение одно, и, если же он больше нуля, то квадратное уравнение имеет два корня.
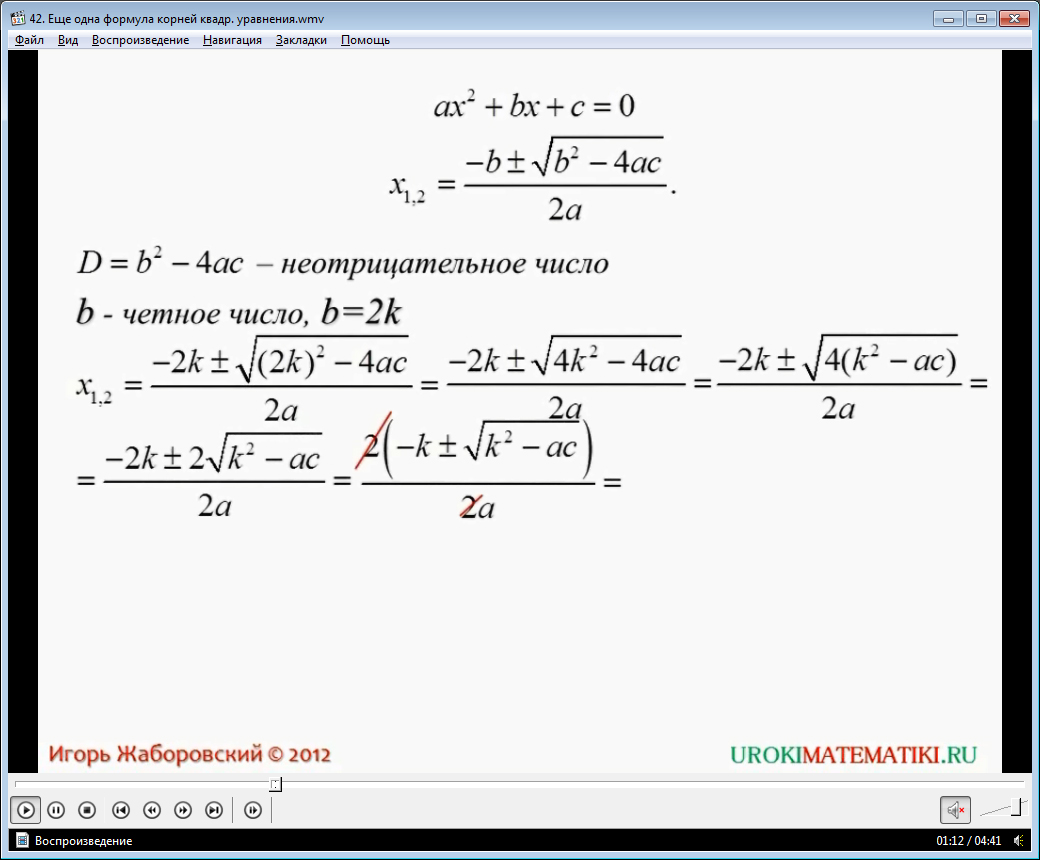
Если коэффициент перед неизвестным в первой степени (обычно b) является четным числом, то можно в разы упростить себе задачу и воспользоваться более упрощенной и простой формулой. Не стоит забывать, что она подходит исключительно для этого случая. Если это условие не будет выполняться, то формула лишь усложнит решение.
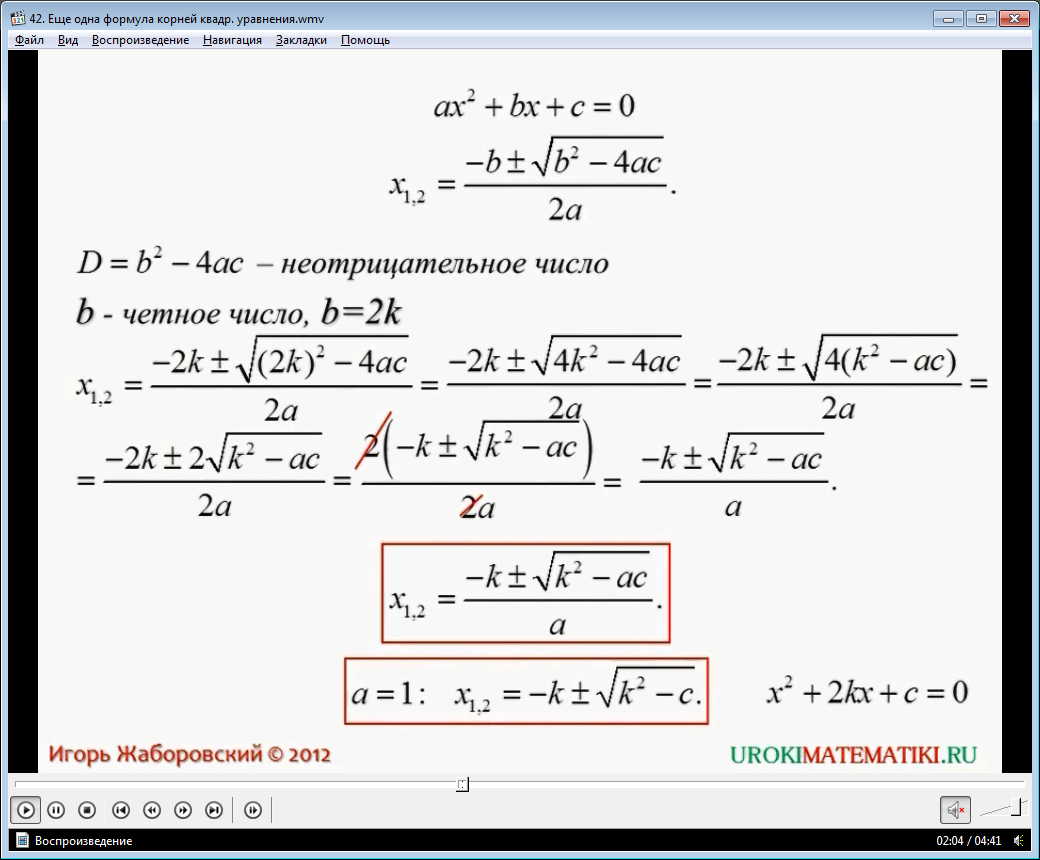
Выводится формула подробным образом, показывает, как поэтапно она получается и почему именно данная формула является истинной. Диктор комментирует каждый шаг, чтобы школьники могли как можно глубже понять суть данного метода. В итоге выводится на экран общий вид формулы, которую стоило бы испытать на практике. Лишь решив большое количество примеров, с использованием данной формулы, можно ее как следует понять и запомнить. Не стоит заставлять учеников зазубривать те или иные методы. Достаточно привести им большое количество примеров и дать возможность самостоятельной работы.
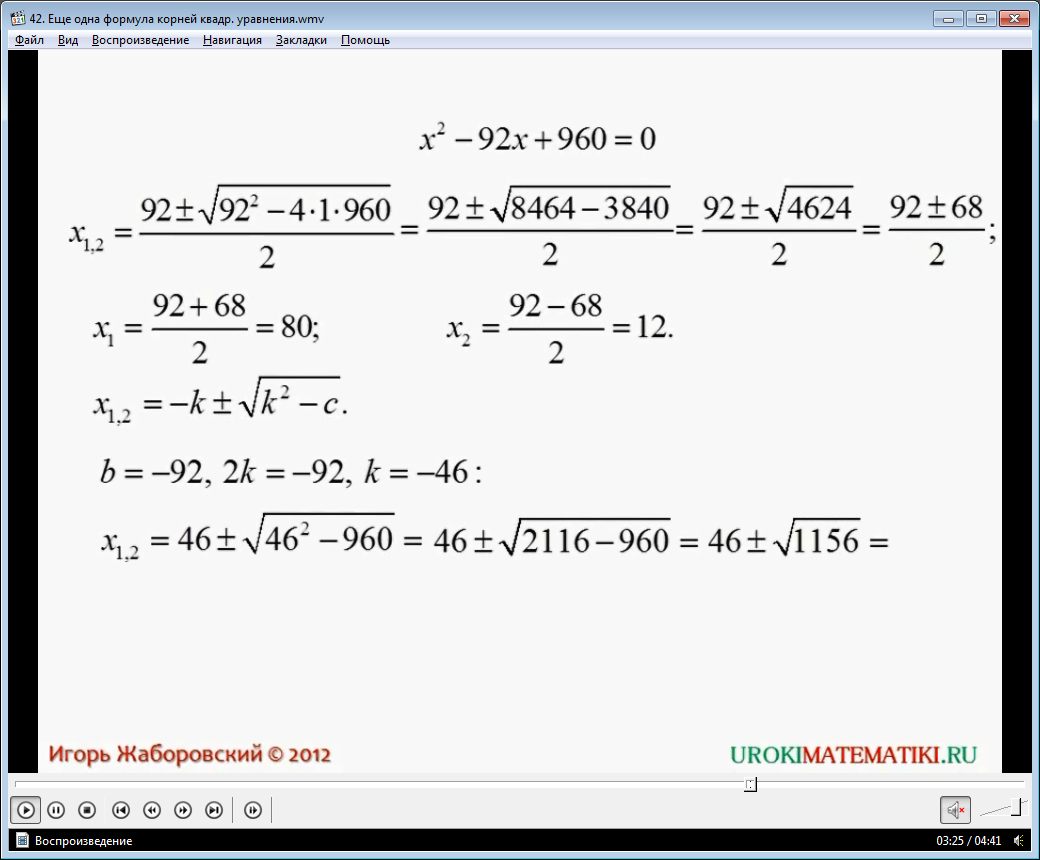
Для того, чтобы школьники могли убедиться в том, что данная формула упрощает решение задачи и сокращает время, в видеоуроке «Еще одна формула корней квадратного уравнения» приводится рассмотрение практических примеров. Если у учеников низкий уровень подготовки, то они могут для начала прорешать те же примеры, решение которых уже просмотрели в видеоуроке. Если уровень достаточно высокий, то они могут приступить к решению квадратных уравнений более высокого уровня.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4967 |
| Номер материала | 564 |