
Урок «Метод координат в пространстве. Координаты вектора»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Для изучения новой темы понадобится определение компланарных векторов.
Векторы называются компланарными, если при откладывании их из одной и той же точки они будут лежать в одной плоскости.
Зададим в пространстве прямоугольную систему координат Охуz. На каждой из положительных осей отложим от начала координат единичный вектор, т. е. вектор, длина которого равна единице.
Обозначим через вектор единичный вектор оси абсцисс, через вектор - единичный вектор оси ординат и через вектор - единичный вектор оси аппликат.
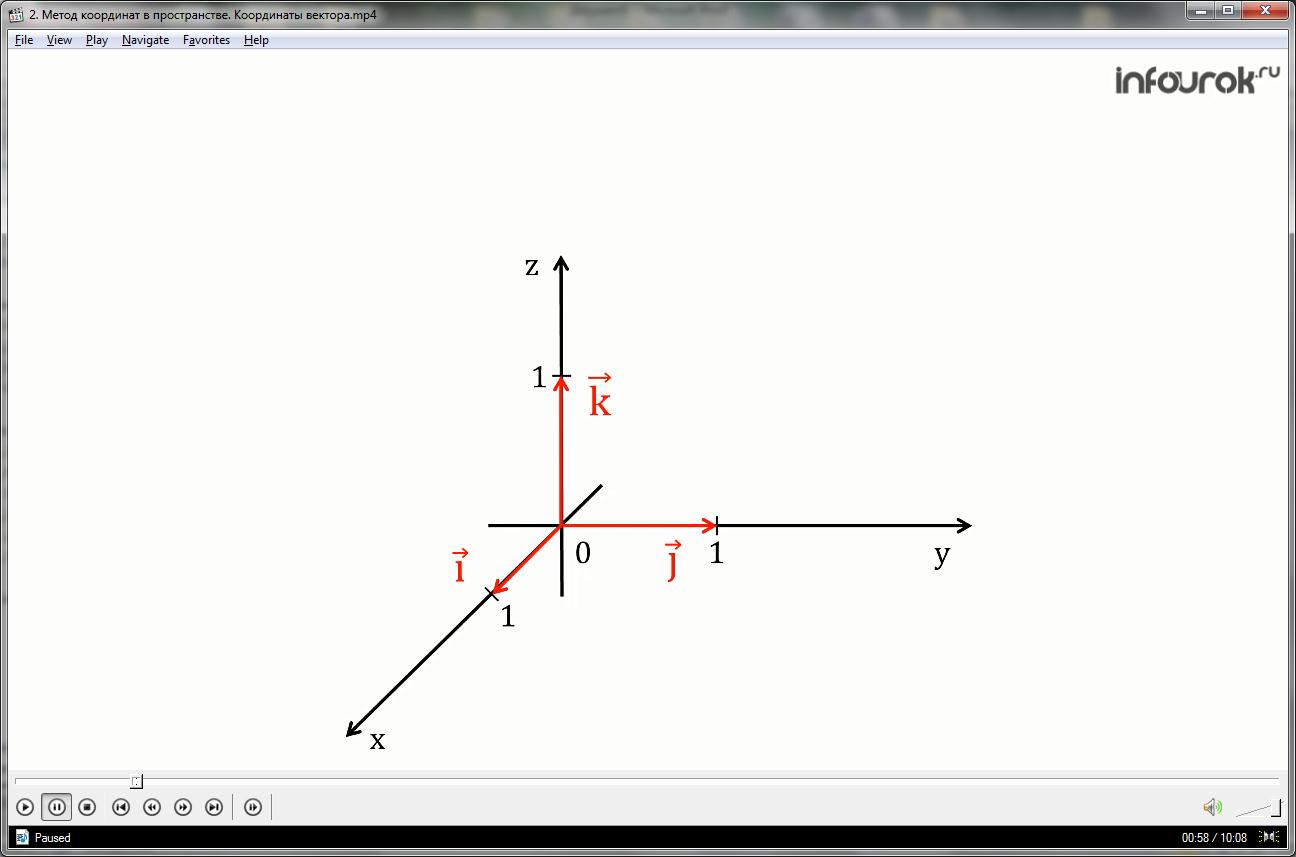
Векторы ,и назовем координатными векторами.
Очевидно, эти векторы не компланарны.
Поэтому любой вектор ( а) можно разложить по координатным векторам, т. е. представить в виде
= х+y+z(вектор а равен: первая координата икс, умноженная на вектор и, плюс вторая координата игрек, умноженная на вектор джи, плюс третья координата зэт, умноженная на вектор ка), причем коэффициенты разложения х, у, z определяются единственным образом.
Коэффициенты х, у и z в разложении вектора по координатным векторам называются координатами вектора в данной системе координат.
Координаты вектора будем записывать в фигурных скобках после обозначения вектора: {х; у; z} (вектор а имеет координаты икс, игрек, зэт; или вектор а с координатами икс, игрек, зэт).
Задача.
Дано.
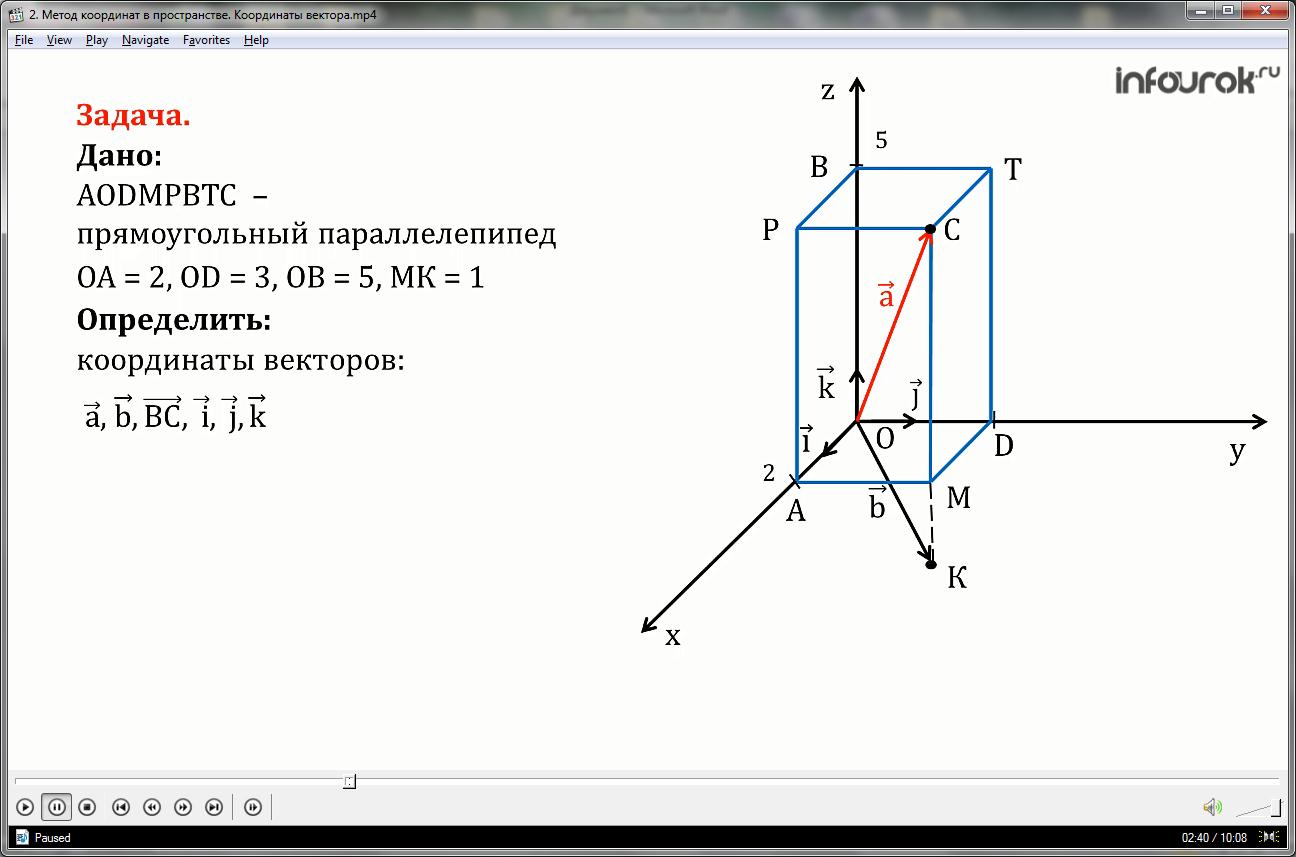
Прямоугольный параллелепипед, имеющий следующие измерения: ОА =2, ОD=3, ОB==5, МК=1.
Определить
Координаты векторов , , , , , .
Координаты радиус-вектора это координаты его конца, получаем координаты вектора а равны координатам точки С, а раз точка С не принадлежит ни одной из координатных плоскостей, то ее координаты равны перпендикулярам на координатные плоскости и соответственно на координатные оси, тогда икс равен проекции точки на ось Ох, для этого опускаем перпендикуляр в точку М и из точки М на Ох, в точку А, получаем длина ОА=2, игрек равен длине ОД=3, так как опускаем перпендикуляр в точку М на плоскость Оху, и из точки М на ось Оу в точку Д, и зет равен длине ОВ=5, опускаем перпендикуляр на ось Оz, в точку B: {2; 3; 5}
Ищем координаты вектора : видим его конец лежит ниже плоскости ОАД, то есть получаем, что зет отрицателен, длина отрезка МК равна 1, тогда зет равен минус одному, икс и игрек соответственно равны длинам отрезков ОА и ОД, т.е. 2 и 3.{2; 3; -1},
Вектор ВС не является радиус-вектором, тогда, что бы найти его координаты, необходимо найти радиус-вектор, равный вектору ВС, и так как отрезок ВС является диагональю верхнего основания параллелепипеда, то радиус-вектор для вектора ВС является вектор ОМ, а его координаты соответственно раны икс равен ОА и = 2, игрек равен ОД и равен 3, и зет равен нулю, так как вектор ОМ лежит в плоскости ОАД, тогда как вектор ВС лежит в параллельной плоскости и зет для векторов этой плоскости равен нулю, (Проекции перпендикуляров из точки В и С на ось Ozпопадают в одну точку В, то есть длина проекции вектора ВС на ось OZравна нулю, поэтому z=0) Координаты вектора ВС равны 2, 3, 0. {2; 3; 0},

Векторы и, джи и ка – это единичные векторы они принадлежат координатным осям, то есть координаты вектора и равны единице, нулю, нулю, так как он принадлежит оси Ох, то его координаты игрек и зет раны нулю, а икс равен единице длина вектора равна единице,{1; 0; 0},
Аналогично вектор джи принадлежит оси Оу, то есть его координаты икс и зет равны нулю, а игрек единице
{(0; 1; 0),
Вектор ка принадлежит оси Оz тогда икс и игрек равны нулю а зет равен единице.{0; 0; 1}.
Так как нулевой вектор можно представить в виде = 0+0+0(нулевой вектор равен: ноль, умноженный на вектор и, плюс ноль, умноженный на вектор джи, плюс ноль, умноженный на вектор ка), то все координаты нулевого вектора равны кулю.
Координаты равных векторов соответственно равны, т. е. если векторы {х₁; у₁; z₁} и {х₂; у₂; z₂} равны, то х₁ = х₂, у₁ = у₂, z₁ = z₂. (если векторы а с координатами икс один, игрек один, зэт один, и вектор бэ с координатами икс два, игрек два, зэт два, равны, то икс один равен икс два, игрек один равен игрек два, зэт один равен зэт два)
Рассмотрим правила, позволяющие по координатам данных векторов найти координаты их суммы, разности и произведения вектора на данное число.
1° Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
Другими словами, если {х₁; у₁; z₁} и {х₂; у₂; z₂} - данные векторы, то вектор + имеет координаты {х₁ + х₂; у₁ + у₂; z₁ + z₂}.
2°. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
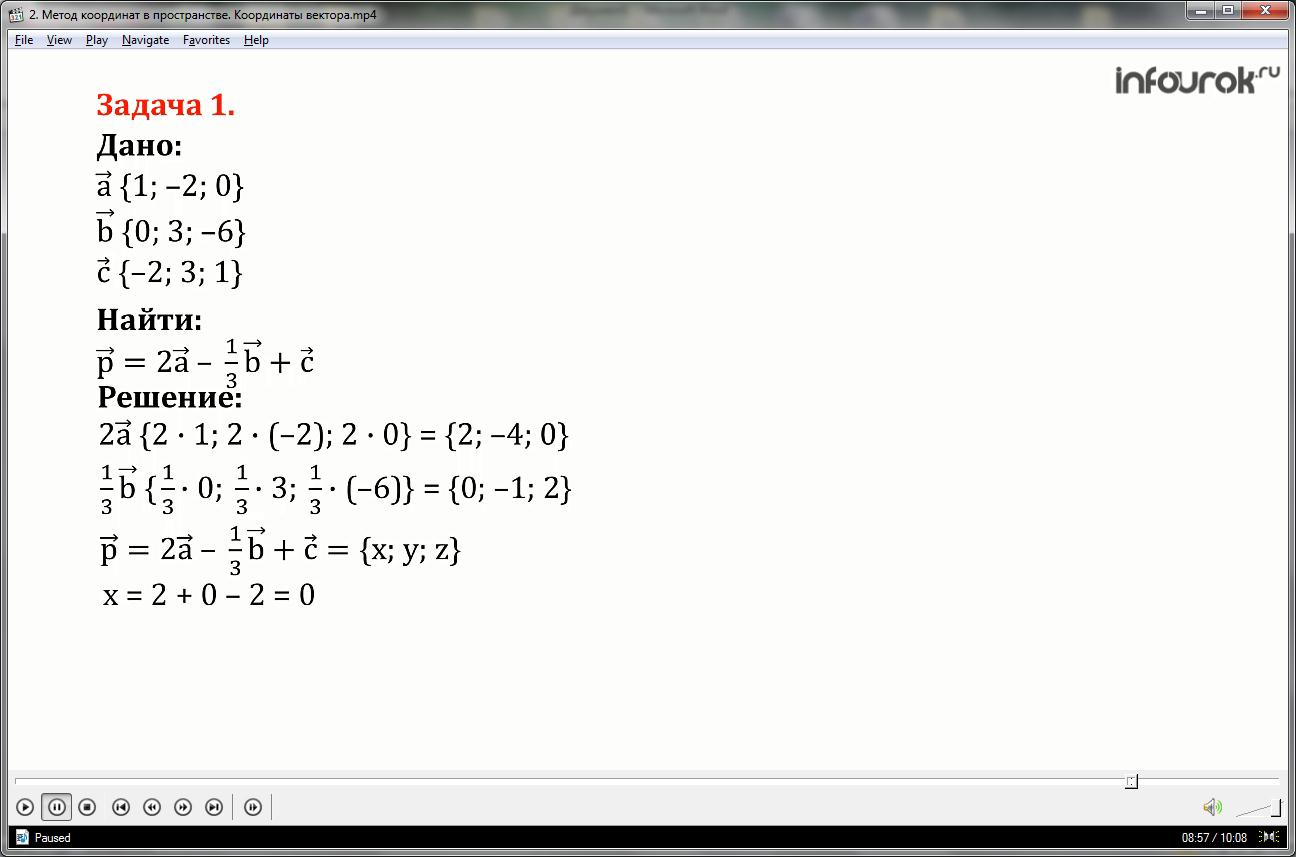
Другими словами, если {х₁; у₁; z₁} и {х₂; у₂; z₂} - данные векторы, то вектор - имеет координаты {х₁ - х₂; у₁ - у₂; z₁- z₂}.
3°. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Другими словами, если {х; у; z} - данный вектор, α - данное число, то вектор α имеет координаты {αх; αу; αz}.
Рассмотренные правила позволяют находить координаты любого вектора, представленного в виде алгебраической суммы данных векторов, координаты которых известны.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 7658 |
| Номер материала | 988 |