
Урок «Метод координат в пространстве. Скалярное произведение векторов»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Для изучения новой темы понадобится повторить теорему о трех перпендикулярах.
Если прямая а, проведенная на плоскости α через основание О наклонной с, перпендикулярна её проекции в, то она перпендикулярна и самой наклонной.
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними. Скалярное произведение двух векторов это число.
Скалярное произведение векторов и обозначается так: (произведение вектора а на вектор бэ).
Таким образом: = ||*||* cos ().
(произведение вектора а на вектор бэ равно произведению модуль вектора а на модуль вектора бэ и на косинус угла между векторами а и бэ)

Справедливы утверждения:
1°. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
≠ , ≠ , = 0 .
Действительно, скалярное произведение вектора на вектор равно произведению их длин на косинус угла между ними. Но cos 90° = 0 следовательно = 0.
2°. Скалярный квадрат вектора (то есть скалярное произведение вектора на себя) равен квадрату его длины.
² = ||²
Действительно, ² =||*|| * cos (). Но cos 0° = 1, следовательно, ² =||*||* 1 = ||²,
Получаем ² = ||²
Скалярное произведение двух векторов можно вычислить через произведение соответственных координат этих векторов:
скалярное произведение векторов {х1; у1; z1} и {х2; у2; z2} выражается формулой:
= х1х2 + у1у2 + z1z2 (скалярное произведение двух векторов равно сумме произведений соответственных координат этих векторов).
Докажем утверждение:
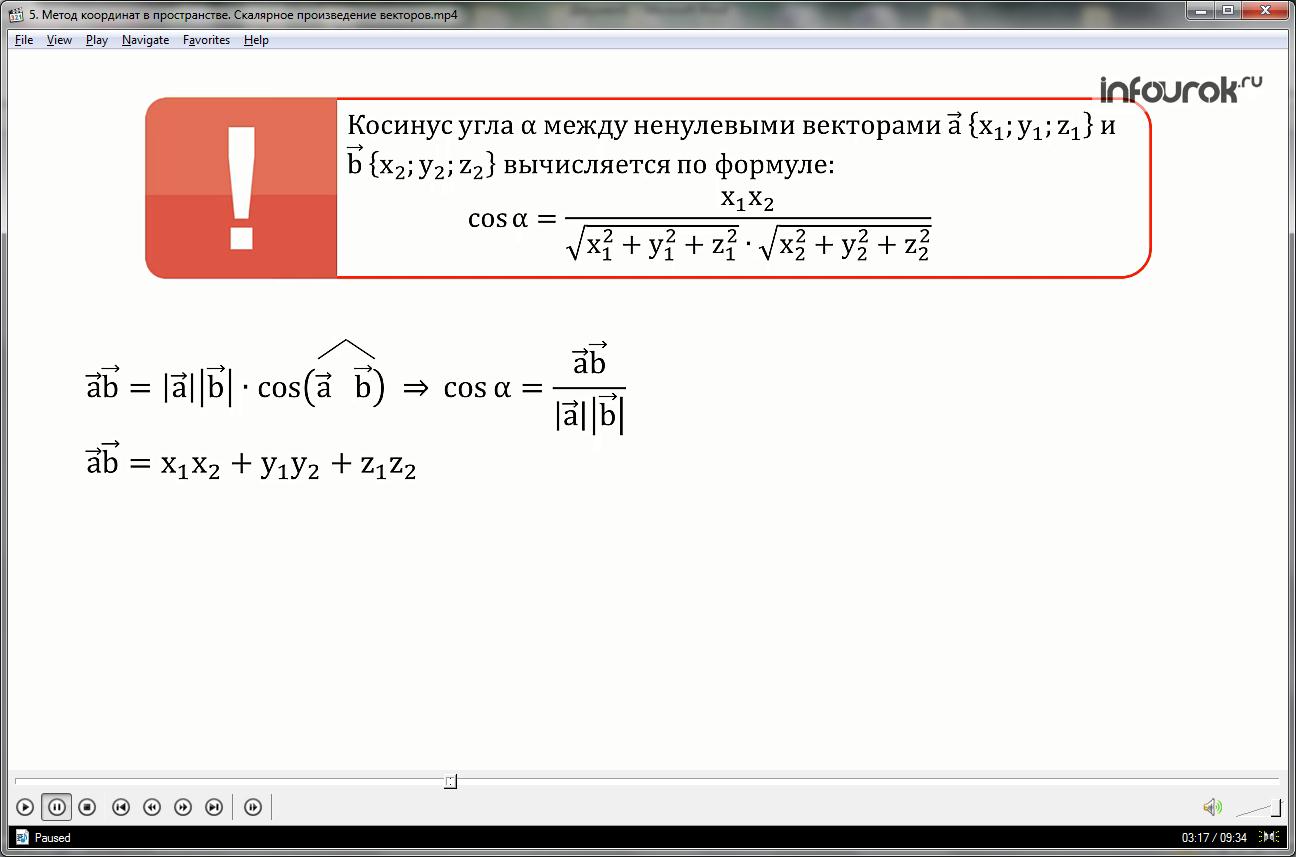
Косинус угла α между ненулевыми векторами {х1; у1; z1} и {х2; у2; z2}
вычисляется по формуле:
cos α = . (Косинус угла альфа равен частному от деления суммы произведений соответственных координат векторов, которые составляют угол альфа, на произведение длин, выраженных координатами этих векторов)
В самом деле, так как = ||*||* cos (), то cos α = (косинус угла альфа равен частному от деления скалярного произведения векторов на произведение их длин).
Таким образом, подставив вместо скалярного произведения формулу суммы произведений соответственных координат векторов х1х2 + у1у2 + z1z2 , а также заменив произведение длин векторов ||*|| на произведение длин векторов, выраженных через координаты
Получим: косинус угла альфа равен частному от деления скалярного произведения векторов на произведение их длин, отсюда следует, что косинус угла альфа равен частному от деления суммы произведений соответственных координат векторов, которые составляют угол альфа, на произведение длин, выраженных координатами этих векторов
cos α = =
Что и требовалось доказать.
Сформулируем основные свойства скалярного произведения векторов.
Для любых векторов , , и любого числа k справедливо следующее:
1°. Скалярный квадрат вектора всегда больше либо равен нулю: ² 0, причем ² > 0 при ≠ 0.
2°. = (переместительный закон – от перестановки мест векторов в скалярном произведении скалярное произведение не меняется).
3°. (+) = + (распределительный закон – скалярное произведение суммы двух векторов на третий вектор равно сумме скалярных произведений каждого из двух векторов на третий ).
4°. k ()=(k) (сочетательный закон – постоянную величину можно вынести за скобки скалярного произведения).
Задача 1
Даны векторы , , ,
Доказать равенство:
( + + ) = + +
Доказательство:
Сумму трех векторов , , можно записать так:
+ + = ( + ) + .
Пользуясь распределительным законом (3°) скалярного произведения векторов, получаем:
( + + ) = (( + ) + ) = ( + ) + = + +
Получили
(++)=++
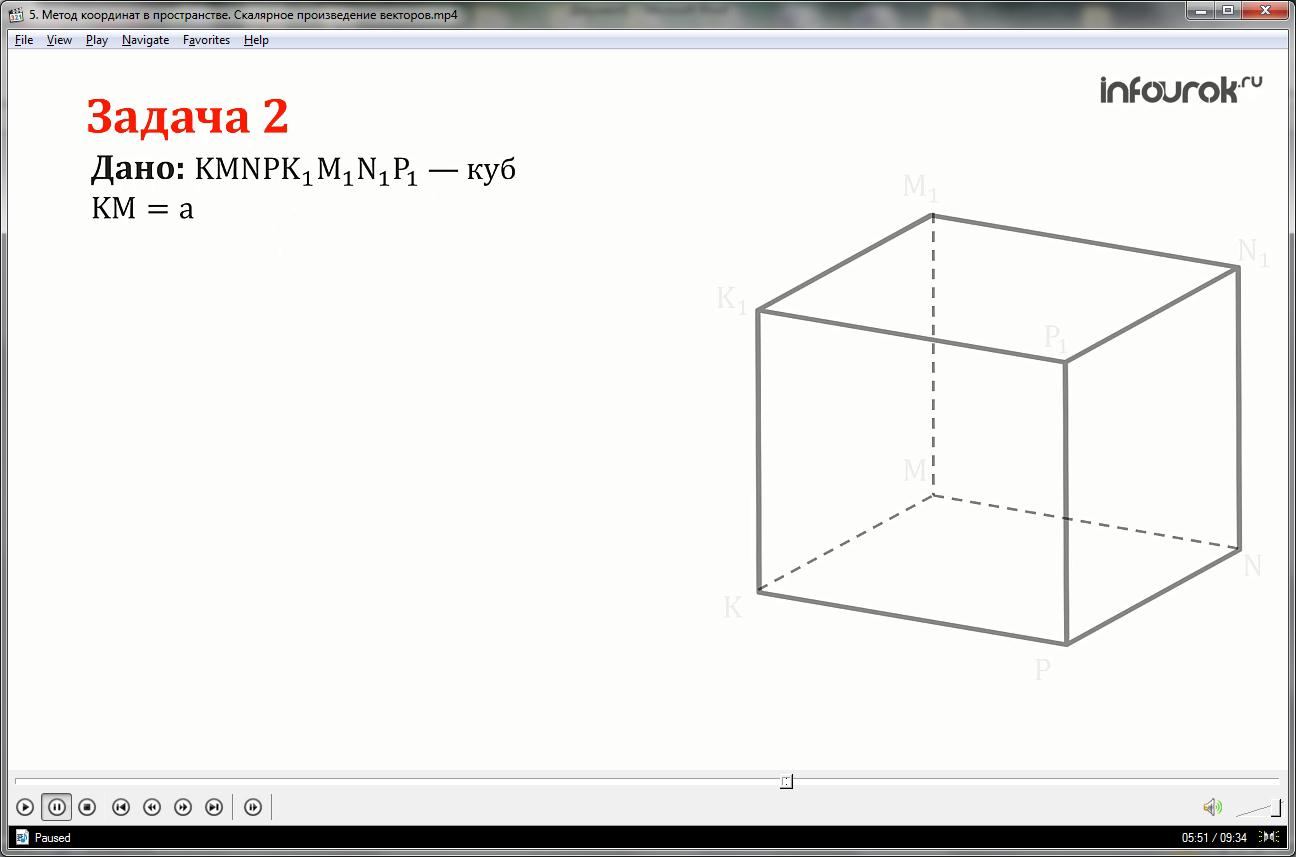
Задача 2
Ребро куба KMNPK1M1N1P1 равно а. Вычислите скалярное произведение векторов:
и
и
Решение.
Длины векторов , равны длинам сторон куба, следовательно, равны а и так как
|| , то cos () = 1,
Получаем скалярное произведение векторов* равно а².
Длины векторов , равны длинам диагоналей граней куба, то есть из теоремы Пифагора получаем, что диагональ грани равна:
|| = || = =
и данные векторы лежат на диагоналях противоположных граней, тогда они коллинеарны, но имеют разное направление, то есть противоположно направлены и угол между ними равен 180 градусов, тогда имеем
cos () = cos 180° = - 1
получаем скалярное произведение векторов KN и N1K1 равно – 2а²
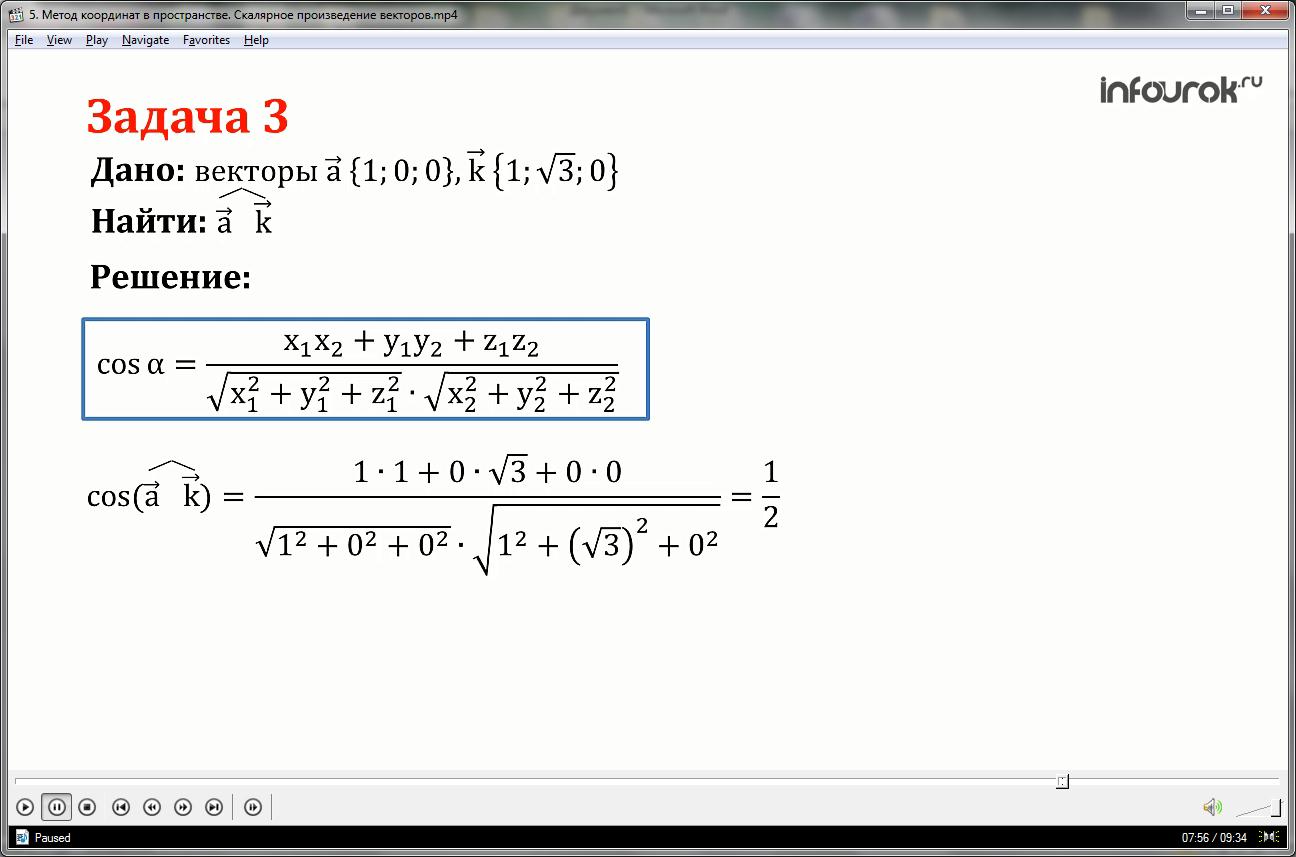
Задача 3
Найти угол между векторами {1; 0; 0} и {1; ; 0}
Решение
Для решения задачи используем формулу:
cos α = .
Подставляем в формулу координаты данных векторов:
cos () = =
(Косинус угла между вектором а и вектором бэ равен частному от деления: в числителе запишем один умножить на один плюс ноль умножить на корень из трех; в знаменателе запишем произведение из квадратных корней, в первом квадратном корне запишем один в квадрате плюс ноль в квадрате; во втором квадратном корне запишем: один в квадрате плюс корень из трех в квадрате. В результате арифметических вычислений получим одну вторую)
Так как cos () = , то угол между векторами а и бэ будет равен арккосинусу одной второй, то есть шестидесяти градусам.
= arcos = 60°
Задача 4
Даны векторы {3; -5; 1} {0; 1; -5} {1; 0; 0} {0; 1; 0}
Вычислить
Решение
Для решения задачи используем формулу:
= х1х2 + у1у2 + z1z2 подставляя соответственные координаты данных векторов, получаем их скалярные произведения:
= 3·0 – 5·1 – 1·5 = - 10
= 3· 1 – 5·0 + 1*0 = 3
= 0·0 + 1·1 – 5·0 = 1
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6190 |
| Номер материала | 991 |