
Урок «Метод координат в пространстве. Связь между координатами векторов и координатами точек»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Повторим понятия
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Если два ненулевых вектора и коллинеарны и если при этом лучи АВ и СD сонаправлены, то векторы и называются сонаправленными.
Определение

Вектор, конец которого совпадает с данной точкой, а начало - с началом координат, называется радиус-вектором данной точки.
Докажем, что координаты любой точки равны соответствующим координатам ее радиус-вектора.
Обозначим координаты данной точки Cчерез (х; у; z).
Пусть A, D, B — точки пересечения с осями координат плоскостей, проходящих через точку C перпендикулярно к этим осям.
Тогда
= + + (вектор ОЦэ равен сумме векторов ОА, ОДэ, ОБэ)

Докажем, что = х. (вектор ОА равен произведению икс на вектор и)
1.В самом деле, если точка A, лежит на положительной полуоси абсцисс, то х = ОА (то икс равен длине отрезка ОА), а векторы и сонаправлены. Поэтому = OA*=х (вектор ОА равен произведению длины отрезка ОА на вектор и, значит, равен произведению икс на вектор и).
2.Если точка A, лежит на отрицательной полуоси абсцисс, то х = - ОA, а векторы и противоположно направлены. Поэтому = - OA*=х(вектор ОА равен произведению длины отрезка ОА с минусом на вектор и, значит, равен произведению икс на вектор и).
3.Наконец, если точка A совпадает с точкой О, то х = 0, = .
Поэтому х= , и снова справедливо равенство = х.
Таким образом, в любом случае = х.
Аналогично доказывается, что = у, = z.(вектор ОДэ равен произведению игрек на вектор джи, вектор ОБэ равен произведению зэт на вектор ка)
Подставив эти выражения в равенство, получим = х+ у + z.
Отсюда следует, что координаты вектора равны {х; у; z}, т. е. координаты точки М равны соответствующим координатам ее радиус-вектора , что и требовалось доказать.
Докажем утверждение.
Каждая координата вектора равна разности соответствующих координат его конца и начала.
Пусть точка D имеет координаты (х₁; у₁; z₁), а точка C– координаты (х₂; у₂; z₂). Вектор равен разности векторов и.
Поэтому его координаты равны разностям соответствующих координат векторов и. Но координаты векторов и совпадают с соответствующими координатами точек C и D: { х₂; у₂; z₂}, { х₁; у₁; z₁}
Поэтому вектор имеет координаты {х₂ - х₁; у₂ - у₁; z₂ - z₁}.
Итак, каждая координата вектора равна разности соответствующих координат его конца и начала.
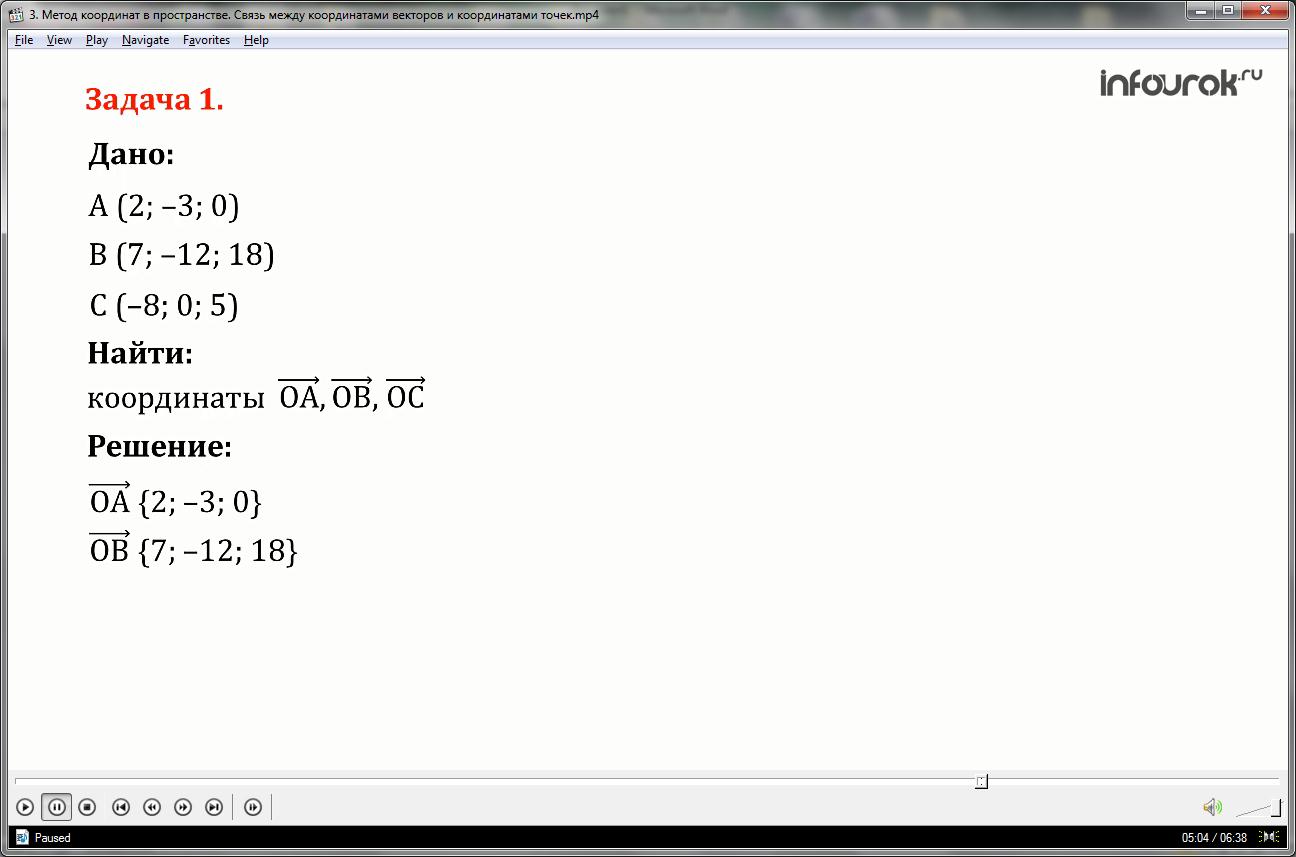
Задача 1.
Даны точки А(2; –3: 0), B(7; –12; 18), C(–8; 0; 5). Запишите координаты векторов , и , если точка О – начало координат.
Решение
По определению, если точка О является началом координат, то векторы , и являются радиус-векторами и их координаты совпадают с координатами их конца, отсюда
{2; –3: 0}, {7; –12; 18} и {(–8; 0; 5}.
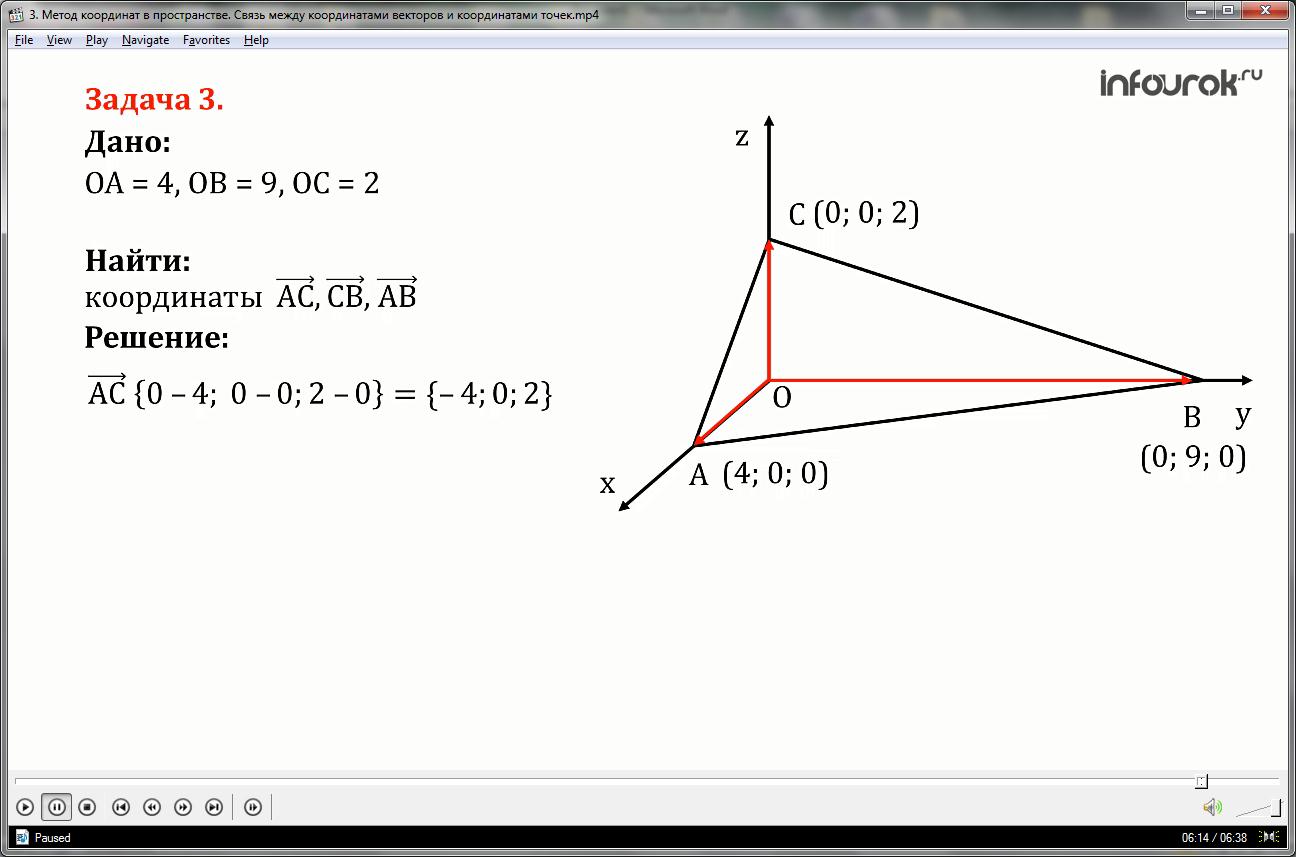
Задача 2.
Найдите координаты векторов, противоположных следующим векторам: Решение:
Противоположные векторы графически имеют противоположное направление, а при записи имеют разные знаки, следовательно, их координаты имеют разные знаки
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 9290 |
| Номер материала | 989 |