
Урок «Метод координат в пространстве. Угол между векторами»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Для изучения новой темы понадобится определение сонаправленных векторов.
Два вектора называются сонаправленными, если они коллинеарны и их направления совпадают.
Возьмем два произвольных вектора и . Отложим от какой-нибудь точки М векторы = и =.
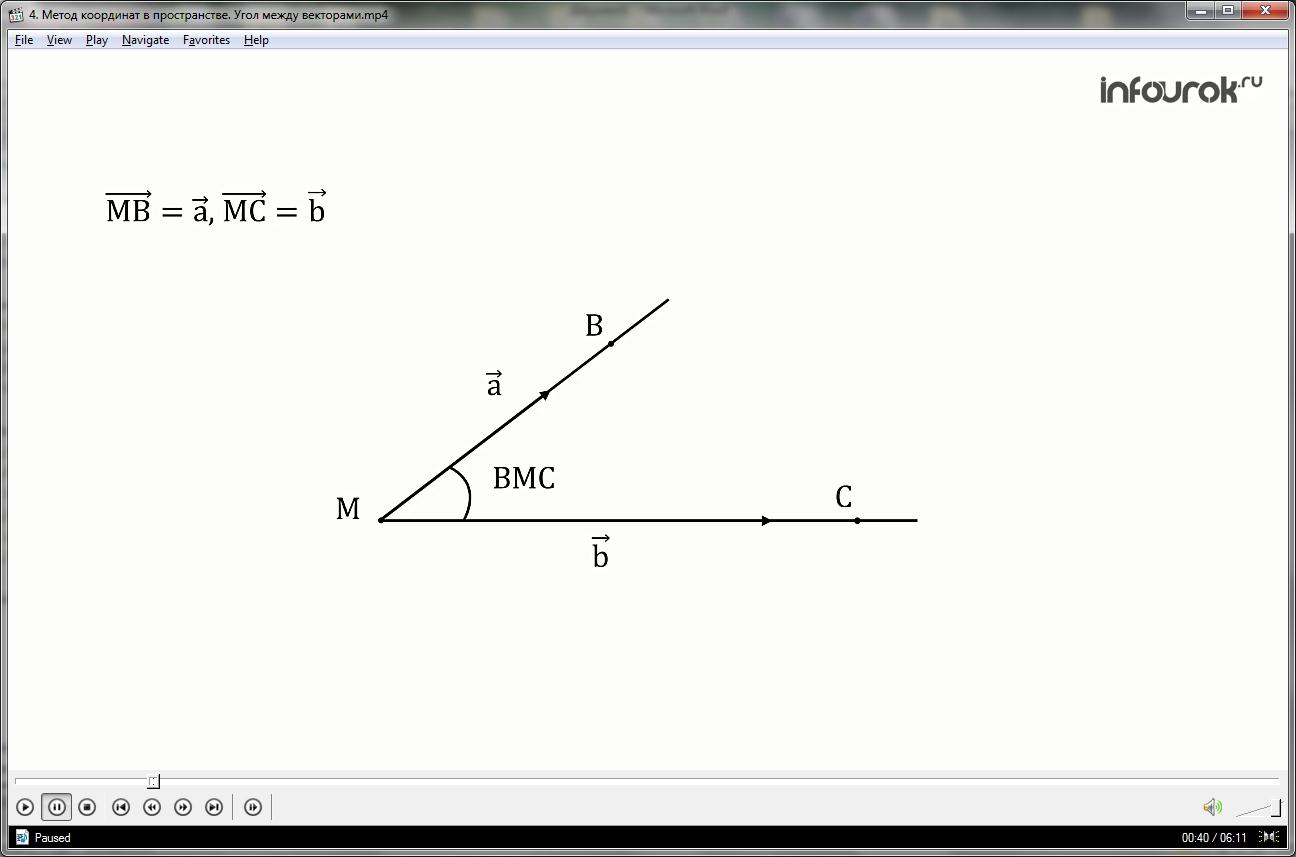
Если векторы и не являются сонаправленными, то лучи МВ и МС образуют угол ВМС. Градусную меру этого угла обозначим буквой α (альфа) и будем говорить, что угол между векторами и равен α.
Если же векторы и сонаправлены, в частности один из них или оба нулевые, то будем считать, что угол между ними равен 0°.
Если угол между векторами равен 90°, то векторы называются перпендикулярными.
Угол между векторами и обозначается так: =.
Пример
Дан угол и векторы , ,,,. Углы между ними таковы : =З0° (угол между векторами а и бэ равен тридцати градусам), =120°, = 90°, = 0°, =180°.
Тогда , , (вектор бэ перпендикулярен вектору цэ, вектор бэ перпендикулярен вектору дэ, вектор бэ перпендикулярен вектору эф).
Рассмотрим простейшие задачи
Задача 1
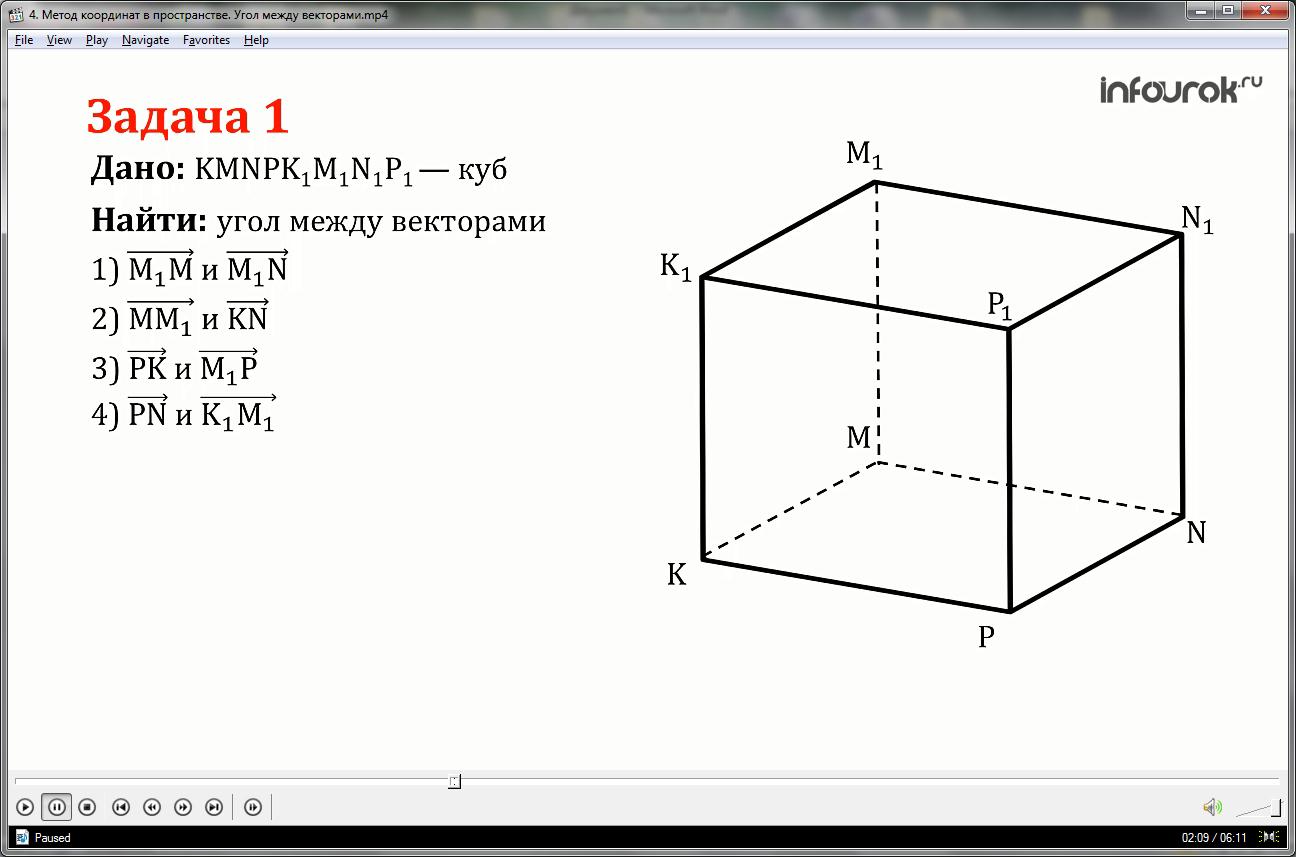
Дан куб KMNPK1M1N1P1.
Найти угол между векторами
- и
- и
- и
- и

Решение
1.Векторы и совпадают с катетом и гипотенузой прямоугольного треугольника MM1N, поэтому = 45°
= = = 90°
Предположим, что сторона куба равна а единицам. Из прямоугольного треугольника КММ1 найдем КМ1. Квадрат гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов. Следовательно, КМ1 = = = =
Векторы и лежат в одной плоскости KM1N1P.
Продолжим прямую М1Р от точки Р на длину вектора . Обозначим конец получившегося вектора точкой С. Тогда = . Следовательно, = .
Найдем . Для этого вычислим величину угла КРС.
КРС = КРО + ОРС, где КРО = 90°, а ОРС = КМ1Р (КМ1 || ОN1, М1С - секущая).
Треугольник КМ1Р – прямоугольный. Следовательно, tgКМ1Р = = (по формуле) → tgКМ1Р = → КМ1Р = ОРС = 45°.
Значит, КРС = КРО +ОРС = 90° + 45° = 135° → = 135°
Следовательно,
= = 135°
= → = 0°
Задача 2
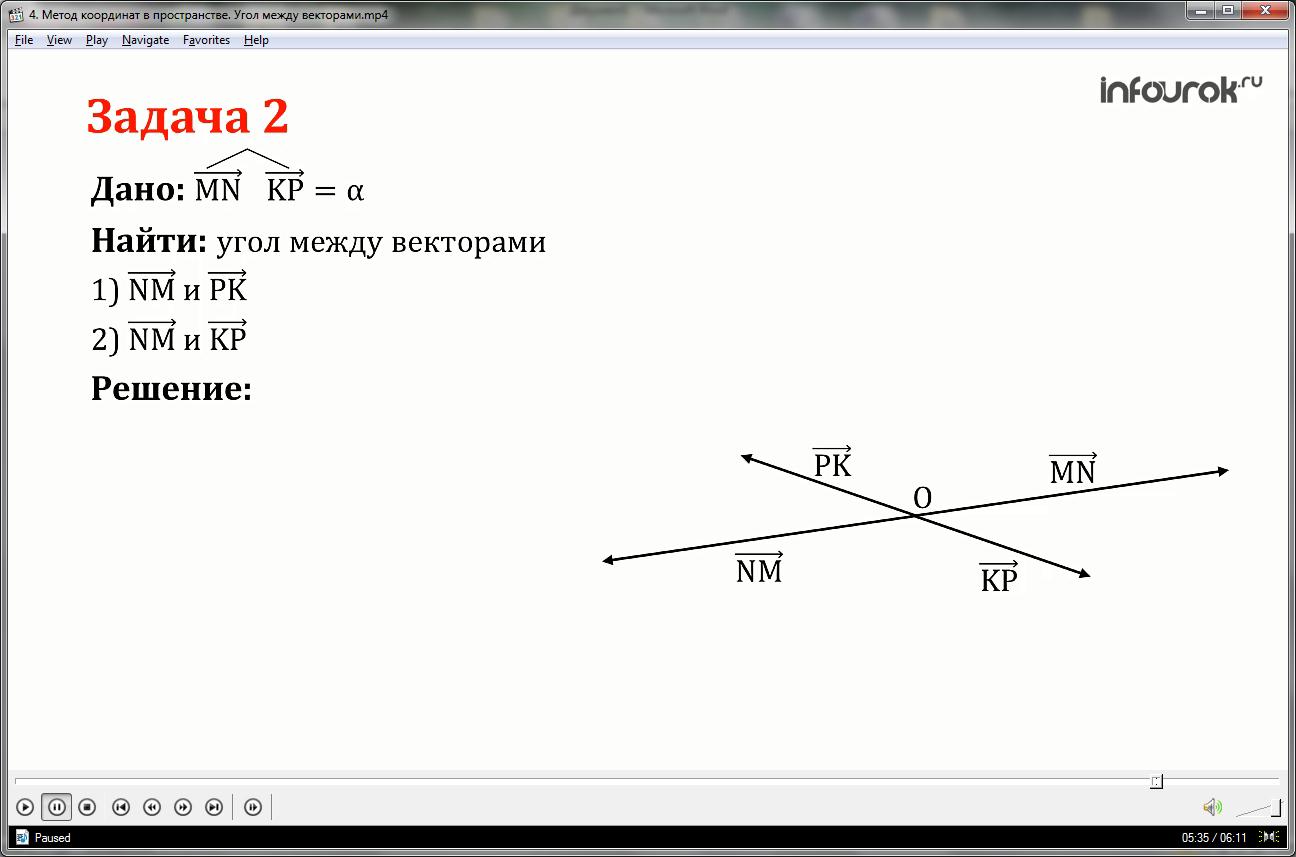
Угол между векторами и равен α.
Найти
Решение
Отложим векторы и от любой точки О и построим векторы и .
Тогда = как вертикальные.
Значит = α
Тогда и - смежные.
Значит = 180° – α
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4045 |
| Номер материала | 990 |