
Урок «Метод координат в пространстве. Вычисление углов между прямыми и плоскостями»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Повторим понятия
Углом α между прямой а и плоскостью γ называется угол между прямой а и ее проекцией (прямая с) на эту плоскость.
Для вычисления угла между двумя прямыми, а также между прямой плоскостью во многих случаях удобно использовать скалярное произведение векторов.
Введем понятие направляющего вектора прямой.
Ненулевой вектор называется направляющим вектором прямой а, если он лежит либо на прямой а, либо на прямой, параллельной прямой а.
Рассмотрим типовые задачи на вычисление углов между прямыми и плоскостями.
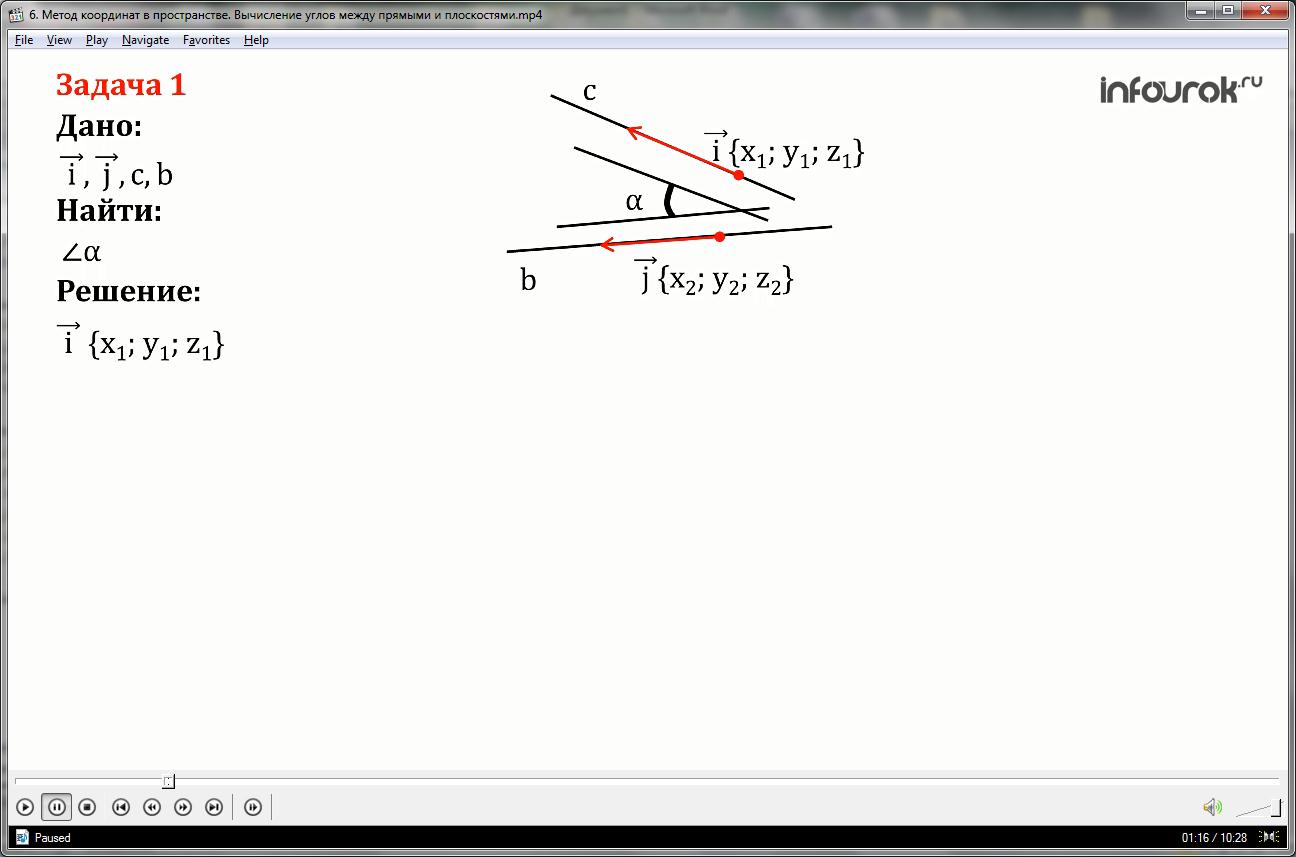
Задача 1
Найти угол между двумя прямыми (пересекающимися или скрещивающимися), если известны координаты направляющих векторов этих прямых.
Решение
Пусть вектор {х1; у1; z1} ( Пусть вектор и имеет координаты икс один, игрик один, зэт один) и вектор {х2; у2; z2} (джи имеет координаты икс два, игрик два, зэт два) - направляющие векторы прямых с (цэ) и b (бэ). Обозначим буквой α (альфа) искомый угол между этими прямыми.
Для решения задачи достаточно найти косинус угла альфа cos α , так как значение соs α позволяет найти сам угол α.
Рассмотрим два случая:
1.Угол фи между векторами и и джи меньше 90 градусов, то есть острый.
Тогда угол φи между вектором и и вектором джи равен углу альфа между прямыми це и бэ. По формуле скалярного произведения векторов найдем косинус угла фи, который равен частному от деления скалярного произведения векторов на произведения их длин:
cos α = cos =
2. Угол фи между векторами и и джи больше 90 градусов, то есть тупой.
В этом случае угол альфа между прямыми це и бэ равен 180° минус угол фи.
Тогда косинус угла альфа равен косинусу угла 180 градусов минус угол фи и равен минус косинус угла фи.
cos α = cos (180° - )= - cos
по определении косинуса если угол альфа меньше 90 градусов, то косинус всегда положителен, следовательно для любого угла альфа имеем косинус альфа равен модулю косинуса угла фи
а зная координаты векторов и и джи свободно можем найти косинус угла альфа
(косинус угла альфа равен частному от деления суммы произведений соответственных координат векторов, которые составляют угол альфа, на произведение длин, выраженных координатами этих векторов)
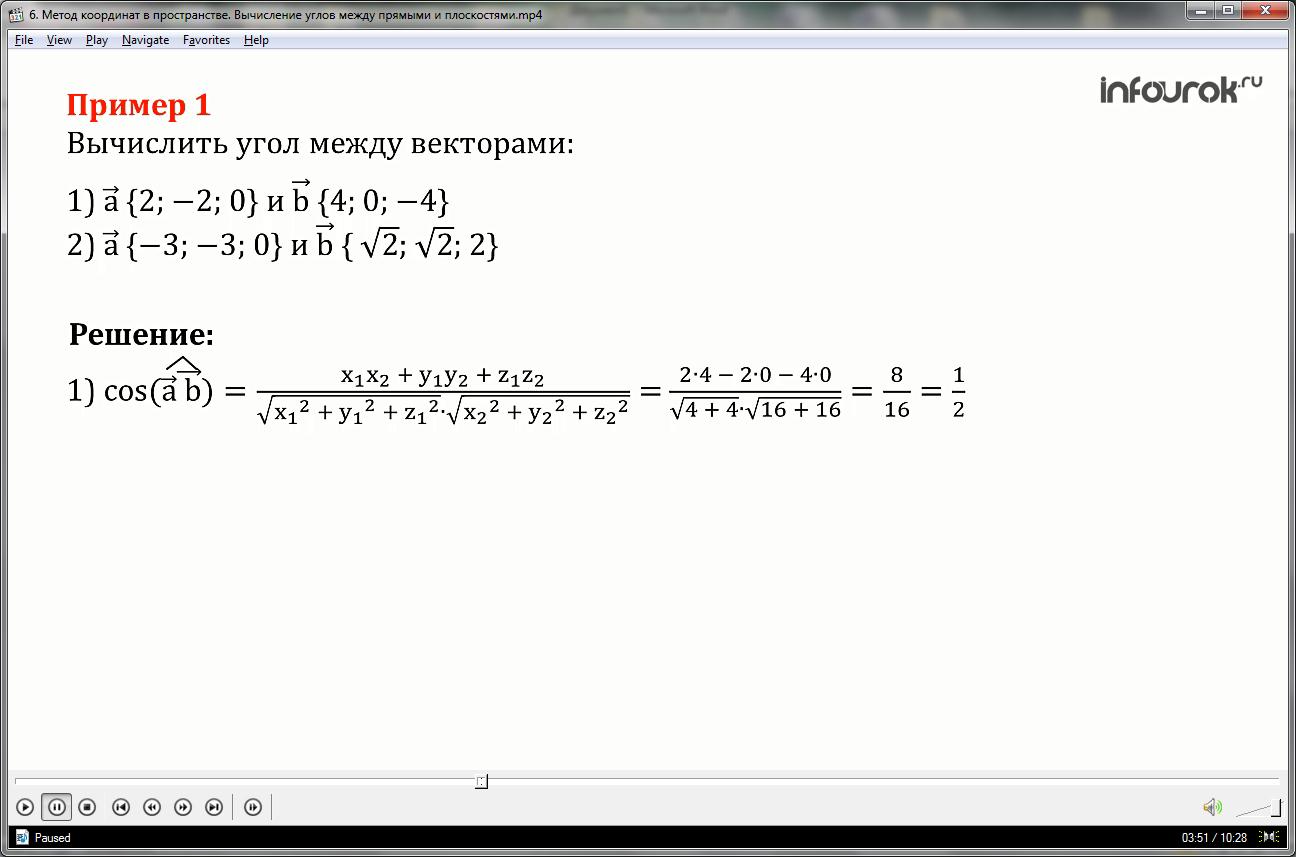
Пример 1
Вычислить угол между векторами
1.{2; -2; 0} и {4; 0; -4} (вектор А с координатами 2,-2,0) и вектор бэ с координатами 4,0, -4)
2. {-3; -3; 0} и { ; ; 2}
Решение
Воспользуемся формулой
cos ( ) = =
= = = (косинус угла между векторами а и бэ равен частному от деления суммы произведений соответственных координат векторов на произведение длин, выраженных координатами этих векторов и, подставляя координаты векторов а и бэ, равно частному от деления: в числителе 2 умножить на 4 минус 2 умножить на 0 минус 4 умножить на 0 в знаменателе: корень квадратный 4 плюс 4 умножить на корень квадратный 16 плюс 16. После арифметических вычислений это равно восемь шестнадцатых или одна вторая)
cos ( ) = , - острый угол
= 60° (угол между векторами а и бэ равен шестидесяти градусам)
2) cos ( ) = =
= =
cos ( ) = , - тупой угол
= 180° - 45° = 135° (угол между векторами а и бэ равен 180 градусов минус 45 градусов и равен ста тридцати пяти градусам)
Пример 2
Вычислить угол между векторами и , если известно, что К (1; 3; 0), Р (2; 3; -1), N (1; 2; -1)
Решение
Вычислим координаты векторов и .
Для этого из соответственных координат последней точки вектора вычтем координаты первой точки.
{1-1; 3-2; 0+1} (координаты вектора ка пэ будут следующими: один минус один, три минус два, ноль плюс один)
{0; 1; 1}
{2-1; 3-2; -1_1}, {1; 1; 0}
По формуле вычисляем
cos ( ) = =
= = → = 60°
(косинус угла между векторами ка пэ и ка эн равен частному от деления суммы произведений соответственных координат векторов на произведение длин, выраженных координатами этих векторов и, подставляя соответственные координаты, равно частному от деления в числителе: ноль плюс 1 плюс ноль в знаменателе корень квадратный из суммы один и один умноженный на корень квадратный из суммы один и один. После вычислений получим одну втору. Из этого следует, что угол между векторами ка пэ и ка эн равен шестидесяти градусам)
Задача 2
Найти угол между прямой и плоскостью, если известны координаты направляющего вектора прямой и координаты ненулевого вектора, перпендикулярного к плоскости.
Решение
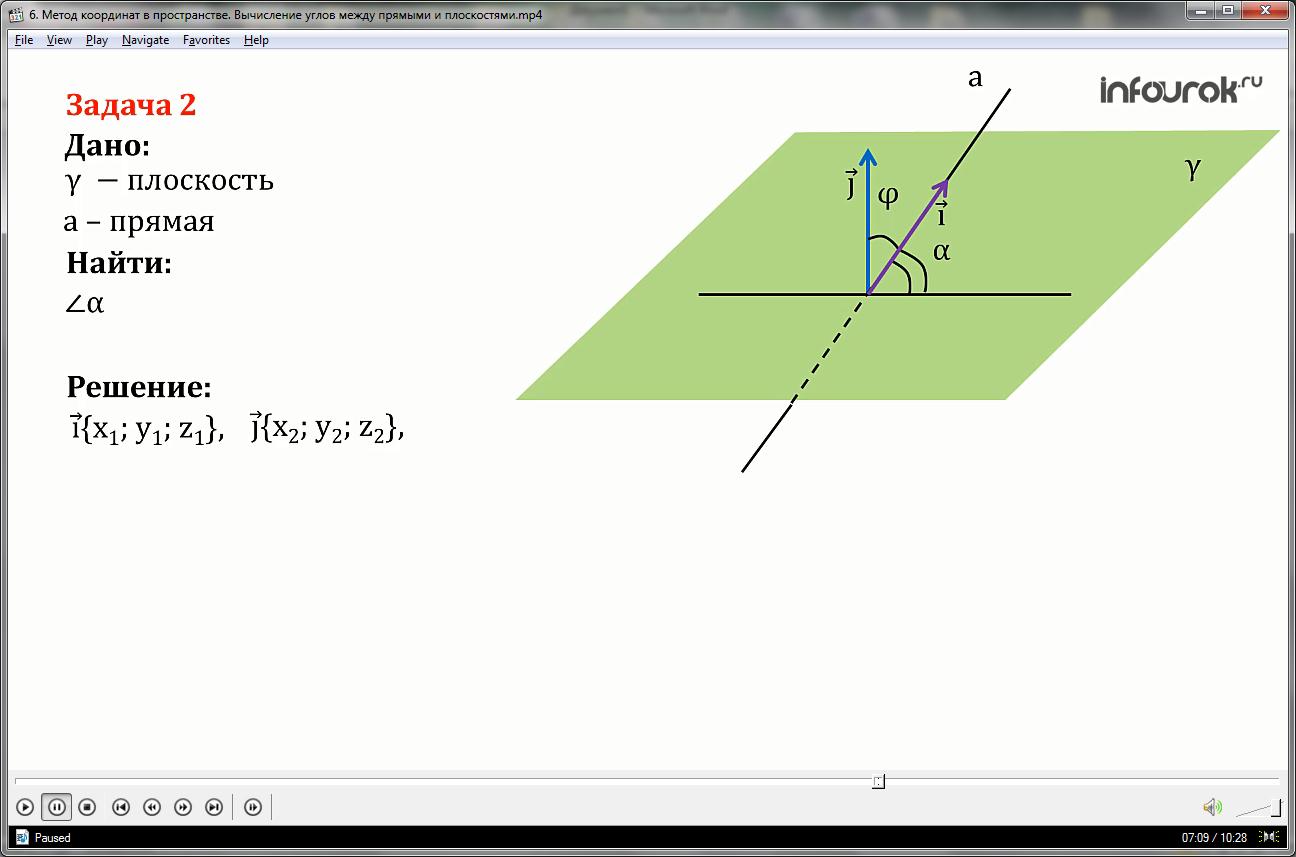
Пусть вектор (и), имеющий координаты { х1; у1; z1} - направляющий вектор прямой а, вектор (джи), имеющий координаты { х2; у2; z2} – ненулевой вектор, перпендикулярный к плоскости γ (гамма). Это означает, что прямая, на которой лежит вектор , перпендикулярна к плоскости γ (гамма). Прямая а не принадлежит плоскости гамма, а пересекает ее в какой то точке.
Обозначим буквой альфа искомый угол между прямой а и плоскостью гамма, а буквой фи - угол между векторами и и джи .
Тогда угол альфа мы можем выразить через угол фи: синус угла альфа равен косинусу угла фи по модулю sin α = |cos |
Можно записать следующую формулу: синус угла альфа равен косинусу угла 90 градусов минус альфа, что равно косинусу угла фи и равно частному от деления произведения векторов и и джи на произведения их длин.
sin α = cos (90° - α) = cos = – (синус угла альфа равен косинусу угла 90 градусов минус альфа равно косинус угла фи равен минус частное от деления произведения векторов на произведения их)
Используя формулу косинуса угла между векторами, записанную через координаты векторов, которую вы видите на экране, формулу (1), получим следующую формулу (2), синус угла между прямой и плоскостью равен модулю косинуса угла между вектором и и джи.
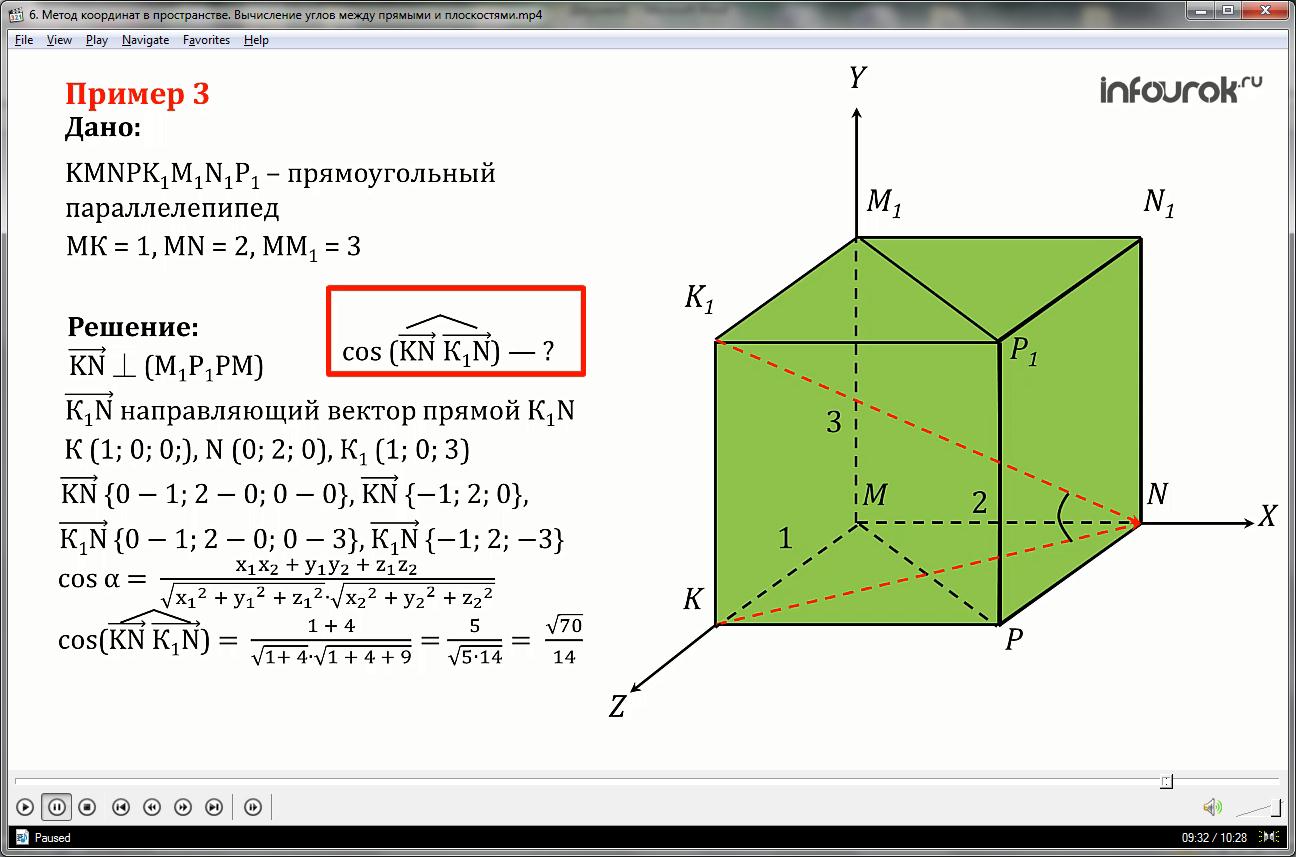
Пример 3
Найти синус угла между прямой К1N и плоскостью М1Р1РМ прямоугольного параллелепипеда KMNPK1M1N1P1 , если известно, что МК = 1, МN = 2, ММ1 = 3.
Решение
Определим, что вектор ка эн КN перпендикулярен данной плоскости эм один пэ пэ эм М1Р1РМ , а вектор ка один эн К1N является направляющим вектором прямой ка один эн.
Таким образом решение сводится к тому, чтобы определить косинус между векторами ка эн и ка один эн.
По данным можно вычислить координаты нужных точек К (1; 0; 0;), N (0; 2; 0), К1 (1; 0; 3)
Тогда координаты векторов будут равны:
{0-1; 2-0; 0-0} {-1; 2; 0},
{0-1; 2-0; 0-3} {-1; 2; -3}
По формуле (1) вычислим
соs ( ) = =
= = (косинус угла между векторами ка эн и ка один эн равен частному от деления в числителе: один плюс четыре в знаменателе корень квадратный из суммы чисел один, четыре и девять умноженный на корень квадратный из суммы один и четыре. После вычислений получим дробь, в числителе которой пять, а в знаменателе произведение из корней квадратных, в первом корне – четырнадцать, во втором корне – пять, и это равно дроби в числителе которой стоит корень квадратный из семидесяти, а в знаменателе стоит четырнадцать.)
Но так как синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой и вектором перпендикулярным к плоскости то
sin ( ) = |cos ( )|
(синус угла между прямой ка один эн и плоскостью эм один пэ один пэ эм равен модулю косинуса угла между векторами ка эн и ка один эн)
получаем ответ: sin ( ) = (синус угла между прямой ка один эн и плоскостью эм один пэ один пэ эм равен дроби в числителе которой стоит корень квадратный из семидесяти, а в знаменателе стоит четырнадцать )
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 8185 |
| Номер материала | 992 |