
Урок "Основное свойство алгебраических дробей"

Краткое описание документа:
Видеоурок «Основное свойство алгебраической дроби» знакомит учеников с основным свойством алгебраических дробей. Сравнивая эти правила применительно к обыкновенным и алгебраическим дробям, а также рассматривая примеры использования свойства для решения математических задач, достигается глубокое понимание темы. Видеоурок является наглядным пособием, демонстрирующим понятно и доступно изучаемые тезисы.
С его помощью учитель быстро достигает учебных целей, ему легче сформировать навыки решения задач с использованием основного свойства. Это достигается с помощью инструментов, доступных при составлении видео – анимационных эффектов, озвучивания, выделения цветом, жирным шрифтом. Данное наглядное пособие помогает повысить эффективность урока математики, сформировать понимание основного свойства дроби, особенности его применения для решения математических задач. Видеурок может послужить для наглядности при объяснении учителем темы, а может служить отбельной частью урока.
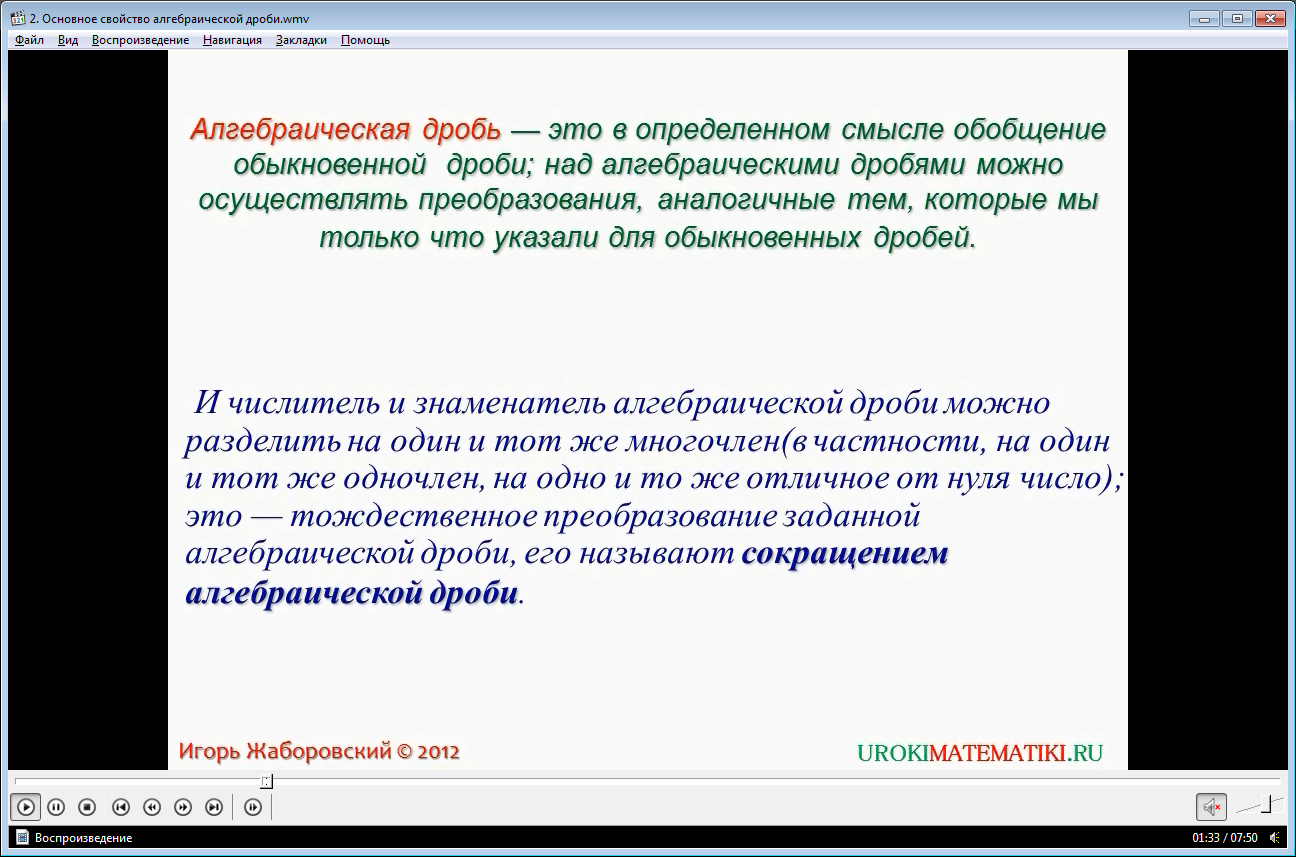
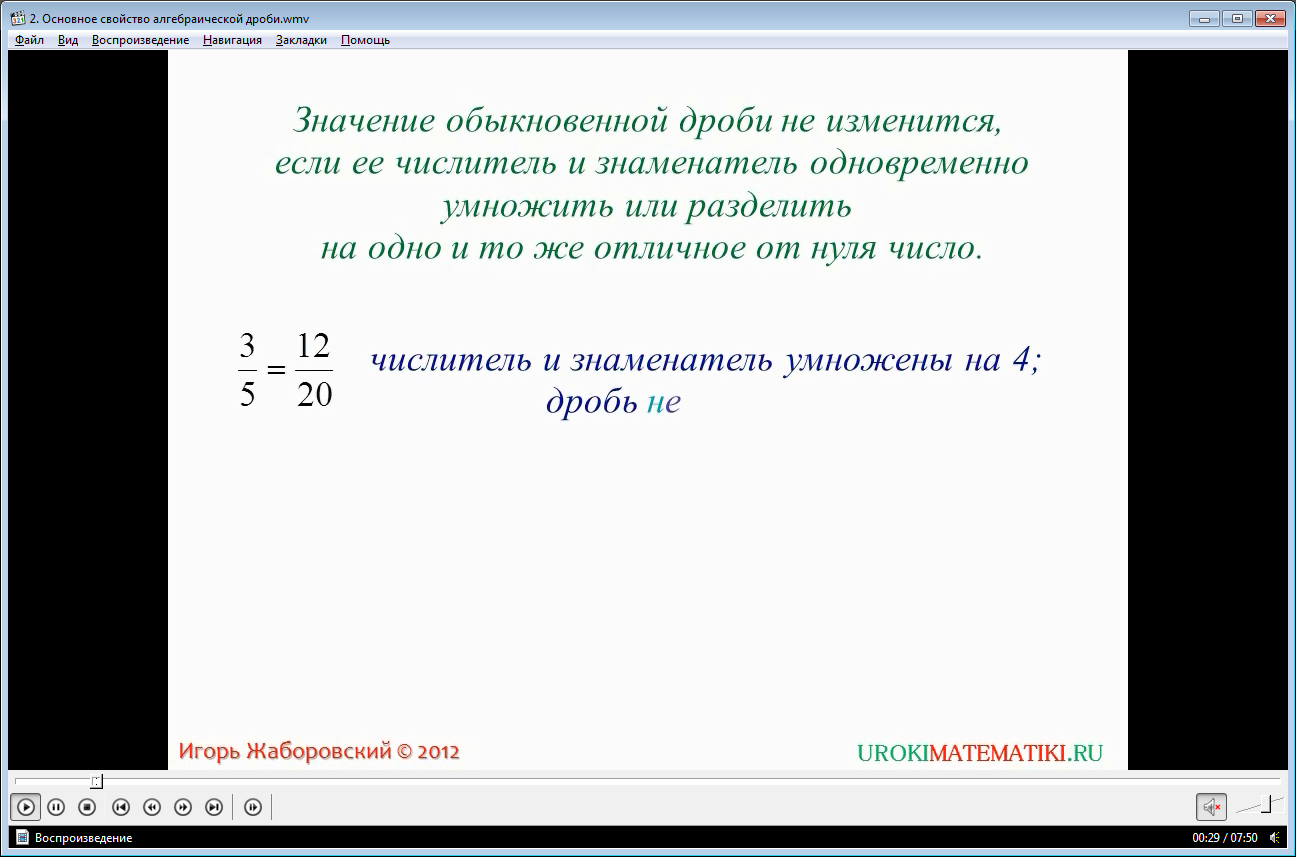
Сначала ученикам напоминается, как звучит основное свойство обыкновенной дроби. Формулировка записана на экране и озвучивается. Для закрепления правила описывается пример сокращения дроби с использованием основного свойства 3/5=12/20. Отмечается, что после выполнения операции умножения числителя и знаменателя на 4, дробь не изменилась. В следующем примере и числитель, и знаменатель дроби делится на число 11. В результате операции значение дроби не меняется 22/33=2/3. Далее уточняется понятие алгебраической дроби и отмечается, что над такой дробью могут выполняться такие же преобразования, как и над обыкновенной. Правило записано на экране, понятие выделено цветом. В соответствии с данным правилом, для алгебраической дроби формулируется основное свойство. В нем отмечается, что знаменатель с числителем такой дроби можно делить на одинаковые многочлены, одночлены, числа (не нуль), и это будет тождественным преобразованием для дроби, иначе называемое сокращением. Чтобы основное свойство легче запоминалось, оно выделено разным шрифтом, название отмечено красным цветом.
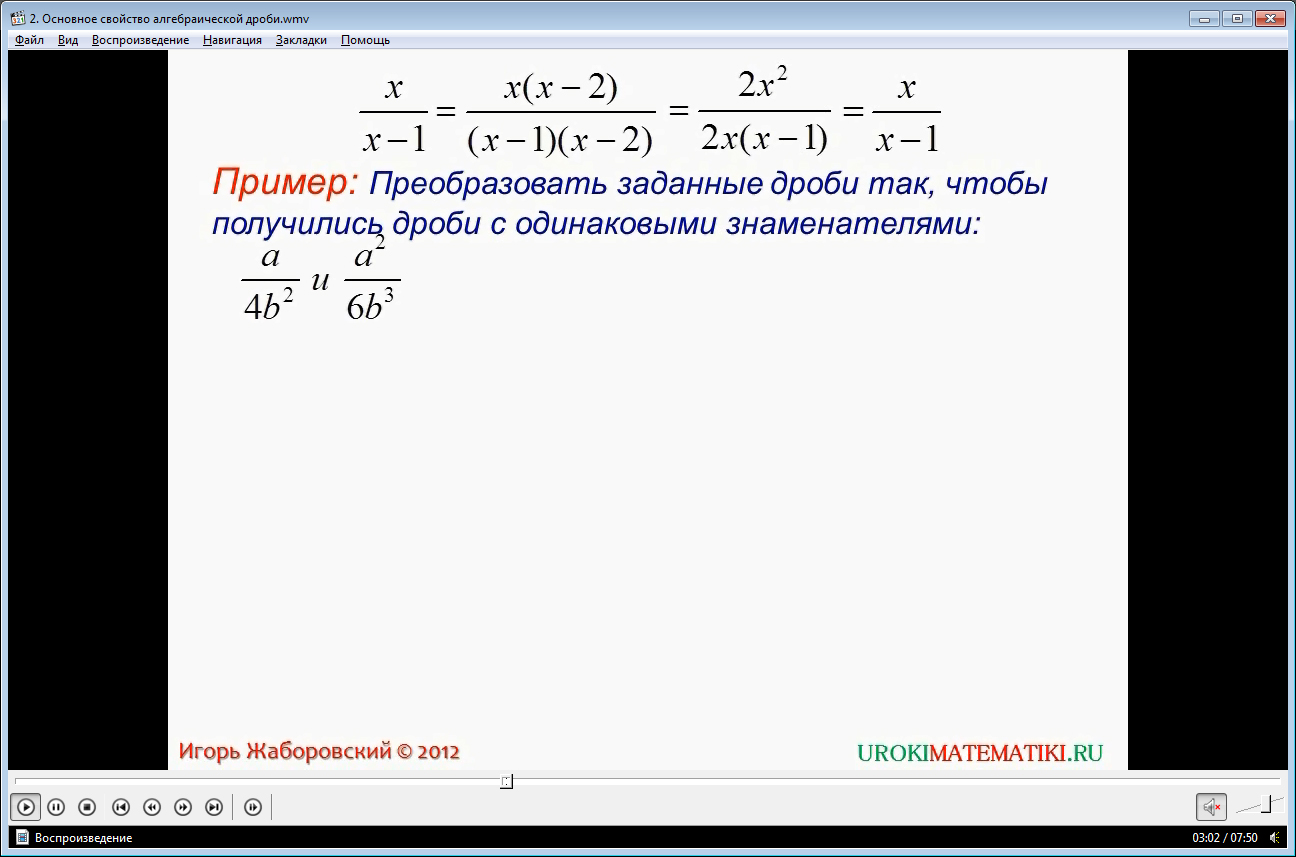
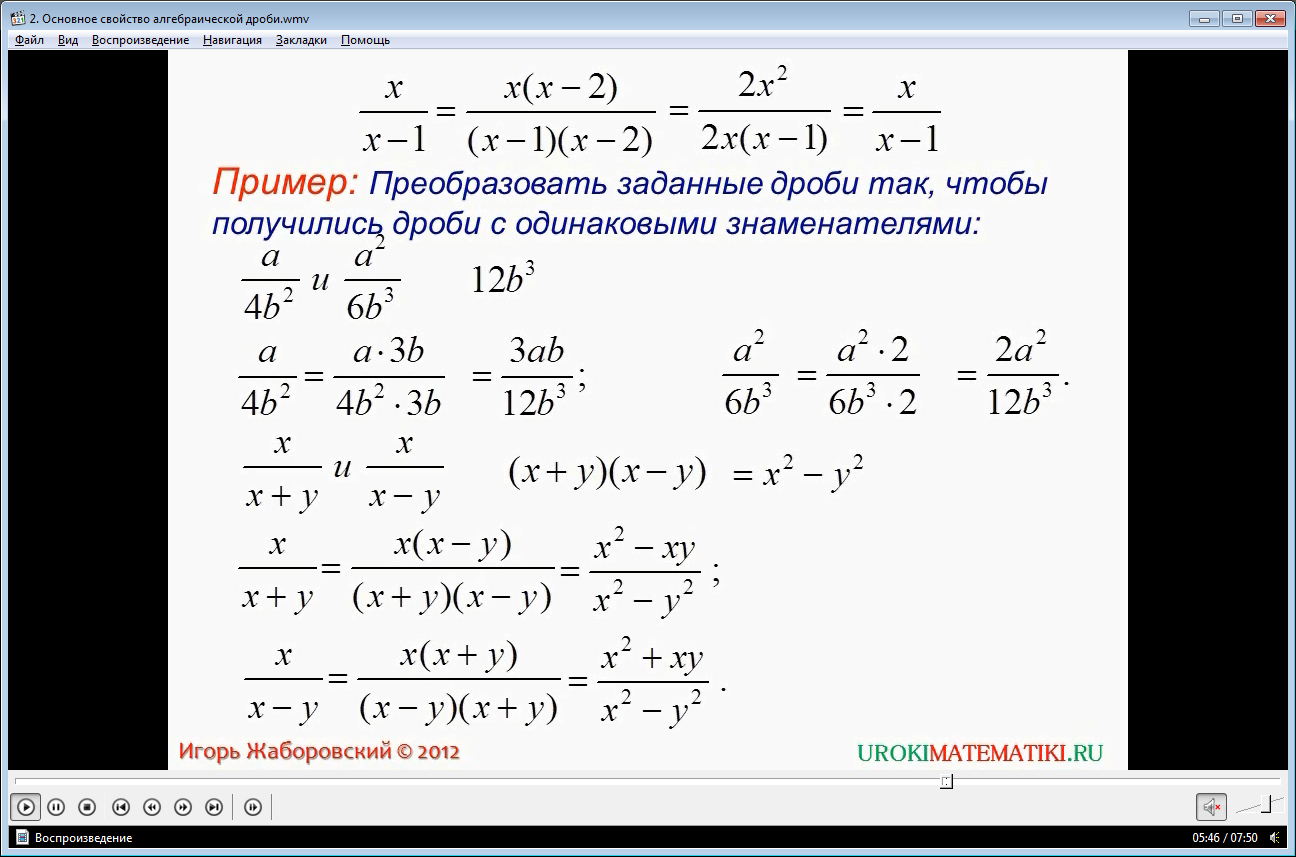
Приводятся примеры, помогающие усвоить материал. На примере умножения частей дроби х/(х-1) на двучлен (х-2) показывается тождественное преобразование исходной дроби путем умножения на многочлен. В результате получается дробь х(х-2)/(х-1)(х-2). Также отмечено, что при умножении исходной дроби на 2х также получаем аналогичную дробь 2х2/2х(х-1). Эта дробь может быть сокращена путем деления числителя со знаменателем на одинаковый одночлен 2х, получая более простой вид дроби х/(х-1). Далее рассматривается пример, когда нужно преобразовать дроби а/4b2 и a2/6b3, чтобы получить одинаковые знаменатели. Отмечается, что общим знаменателем данных дробей является выражение 12b3. Чтобы преобразовать первую дробь, нужно числитель и знаменатель умножить на 3b. В результате получаем равную дробь 3ab/12b3. Вторая дробь умножается на 2, после чего получается равна ей a2/12b3. Отмечается, что такие преобразования стали возможны при действии основного свойства алгебраической дроби.
Аналогичное предыдущему примеру решается задание, в котором нужно привести к общему знаменателю дроби х/(х+у) и х/(х-у). Общий знаменатель определяется произведением знаменателей этих дробей (х+у)(х-у)=х2-у2. Пользуясь основным свойством алгебраической дроби, получаем дробь, равную первой после умножения ее на (х+у), то есть (х2-ху)/( х2-у2). Аналогично производим преобразование второй дроби, умножая ее на (х-у), получаем дробь (х2+ху)/( х2-у2). Отмечается, что в отличие от применения основного свойства для сокращения дроби, рассмотренные преобразования усложнили дроби в обоих примерах. Такое преобразование целесообразно при решении некоторых задач, которые будут рассматриваться дальше.
Рассматриваются правила изменения знаков в дробях. Отмечается, что изменить знаки выражения можно только умножив знаменатель с числителем дроби на число -1. Примером служит дробь (a-b)/(c-d), которая после умножения числителя, а также знаменателя на -1, преобразуется в (b-a)/(d-c). Отмечается также, что при необходимости изменить знак одной части дроби – числителя или знаменателя, меняется знак перед самой дробью. Так указанная дробь может быть преобразована в -(b-a)/(c-d). С помощью анимации подробно объясняется, как меняются знаки частей дроби, и что важно учесть в таких преобразованиях.
Видеоурок «Основное свойство алгебраической дроби» помогает повысить эффективность урока математики по данной теме. Материал может входить в число обучающих инструментов учителя, обучающего учеников дистанционно. Учащимся, которым необходимы дополнительные занятия для освоения темы, урок поможет глубже понять предмет.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6685 |
| Номер материала | 525 |