
Урок "Площадь. Формула площади прямоугольника"

Краткое описание документа:
Видеоурок «Площадь. Формула площади прямоугольника» - наглядное пособие, которое служит для объяснения пятиклассникам основных положений, формирующих понятие площади прямоугольника. В ходе видеоурока рассматривается, как формируется понятие площади, что означает единица измерения площади, описываются общий и частные случаи вычисления площади прямоугольника. С помощью видеоурока учителю легче сформировать понятие о площади фигуры, умение находить площадь прямоугольника. Материал может использоваться самостоятельно как часть урока или сопровождать объяснение учителя. Наглядное пособие поможет быстрее достичь учебных целей, повысить эффективность урока математики.

В видео, чтобы сделать объяснение темы наглядным, используется ряд инструментов. Основной инструмент – это возможность преставления иллюстрированной учебной информации, выделение текста различным шрифтом, вставка анимационных эффектов, дополнение видео голосовыми комментариями. Представление учебного материала в текстовом виде, сопровождая иллюстрациями, дает возможность добиться более глубокого понимания темы. Использование в демонстрации текста цветных шрифтов, выделение важных понятий, использование анимации помогает удерживать внимание учеников на изучении предмета, способствует запоминанию материала. Вставка голосового сопровождения позволяет дополнить видео важными комментариями, благодаря чему видео может использоваться вместо объяснения учителя.

Видеоурок начинается с представления названия темы. Затем вводится понятие площади фигуры. На экране изображается фигура, состоящая из восьми квадратов, каждый со стороной 1 см. Отмечается, что площадь одного квадрат, входящего в фигуру, представляет собой квадратный сантиметр. Вводится условное обозначение единицы измерения площади данной фигуры – 1 см2. Соответственно, площадь данной фигуры 8 см2.
Рассмотренный материал обобщается в правиле, определяющем площадь фигуры. В нем указано, что если фигура может быть разбита на р квадратов, стороны которых 1 см, то площадь фигуры равна р см2.
Далее представлен пример – на экране изображен прямоугольник со сторонами 5 см и 3 см. Прямоугольник разбит на квадраты со стороной 1 см. Таким образом, в составе прямоугольника содержится 15 квадратов – 5 столбиков и 3 ряда. Чтобы найти площадь прямоугольника, нужно найти общее количество содержащихся в нем квадратов, то есть 5·3=15. Значит, площадь данного прямоугольника равна 15 см2. Вывод о способе нахождения площади прямоугольника представлен ниже в виде правила. В нем указано, что для нахождения площади прямоугольника необходимо перемножить его длину и ширину. Правило выделено цветным шрифтом и рекомендовано к запоминанию. Это правило также записывается в виде формулы. Для этого вводятся обозначения параметров: S – площадь прямоугольника, a – его длина и b – ширина. Формула площади прямоугольника S= a·b выделена в рамку и рекомендована к запоминанию.
Разъясняется понятие равных фигур и их свойства. На экране отображается определение равных фигур, в котором равными называются фигуры, совпадающие при наложении. При этом отмечается равенство площадей равных фигур и их периметров. Свойства равных фигур выделены цветным шрифтом для лучшего запоминания.
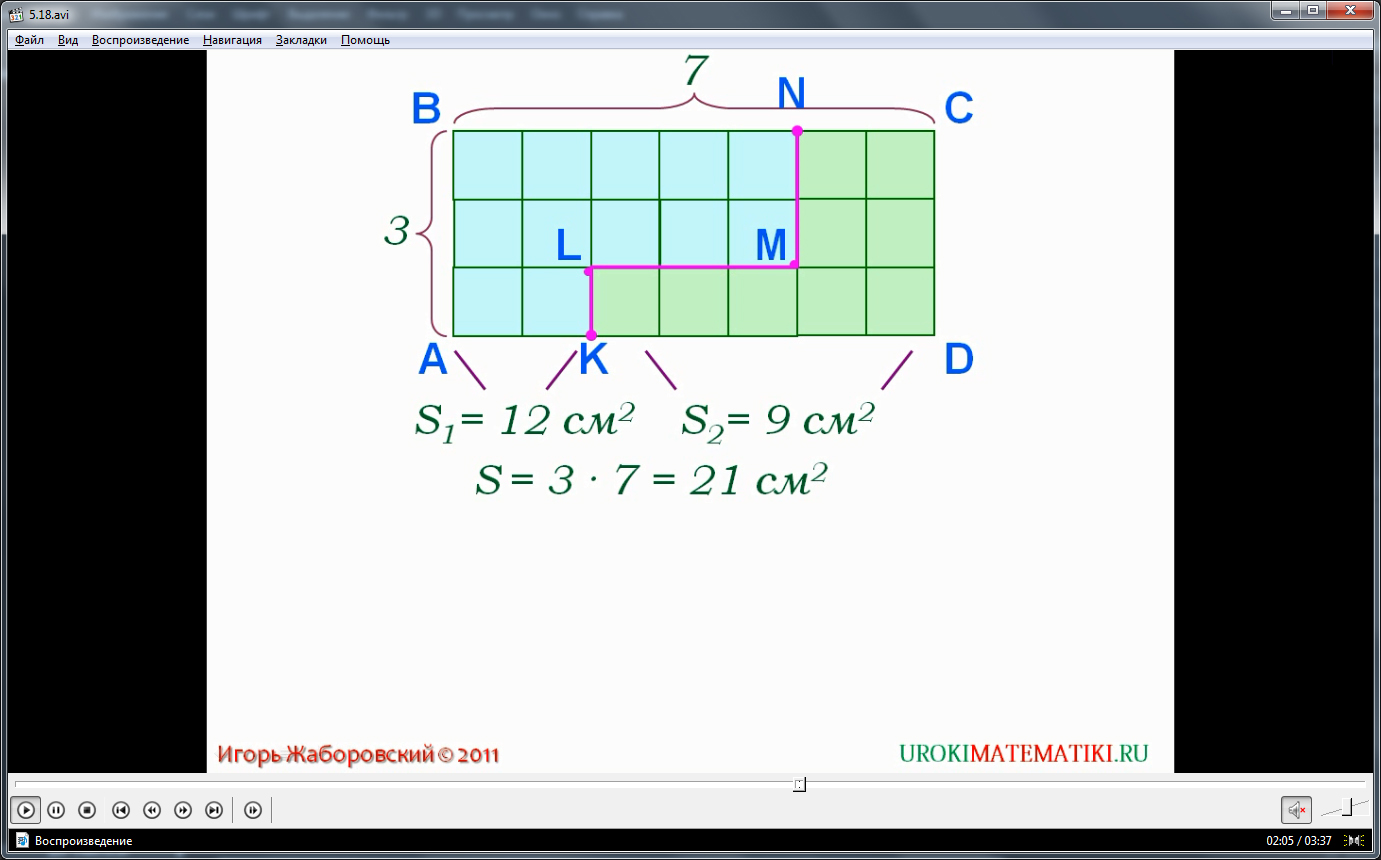
Для закрепления изученного материала рассматривается пример. На экране изображен прямоугольник ABCD, поверхность которого разбита на равные квадраты со стороной 1 см. В прямоугольнике помещается 7 столбцов и 3 ряда квадратов. Через прямоугольник проведена линия KLMN, которая разделяет прямоугольник на две части – в одной содержится 12 квадратов, а во второй – 9 квадратов. Это означает, что площадь первой части 12 см2, а площадь второй части – 9 см2. Вычисляя площадь всей фигуры, отмечается, что для этого нужно перемножить ее длину и ширину – S=3·7=21 см2. При этом можно отметить, что сложив площади фигур, полученных при разрезании линией KLMN, образуется это же значение площади 21=12+9. Это подтверждает правило, которое при обобщении затем выводится для запоминания – площадь всей фигуры равна сумме всех частей этой фигуры. Правило выведено на экран и выделено цветным шрифтом.
Затем рассматривается прямоугольник ABCD, который разбит диагональю АС на две равные части ABC и ACD. Ниже рисунка демонстрируется правило, которе утверждает, что площадь каждого из полученных таким образом треугольников равняется половине площади всего прямоугольника.
Рассматривается нахождение площади квадрата как частный случай задачи на нахождение площади прямоугольника. На рисунке изображен квадрат со стороной 4 см. Ученикам напоминается, что квадратом называется прямоугольник, у которого стороны равны. Зная формулу для нахождения площади прямоугольника, можно найти площадь квадрата S=4·4. Иначе данное произведение записывается 42. Вычислив его, получаем площадь квадрата 16 см2. Информация обобщается в правило, что для нахождения площади квадрата со стороной а необходимо возвести ее значение в квадрат, то есть S=а2. Замечено, что и название «квадрат числа» произошло в связи с этой особенностью приложения математического аппарата.

В конце видеурока предлагается ответить на вопросы для контроля знаний. В числе вопросов такие задания, которые выявляют понимание сути нахождения площади фигуры, насколько хорошо ученики усвоили формулу нахождения площади прямоугольника и квадрата, определение и особенности равных фигур, соотношение площади фигуры и ее частей.
Видеоурок «Площадь. Формула площади прямоугольника» может применяться на традиционном школьном уроке математики для повышения его эффективности. Также материал рекомендуется как наглядное пособие для формирования представления о площади фигуры, умения решать задания на нахождение площади. Если ученику необходимо самостоятельно освоить тему, видео может быть предложено для самостоятельного изучения дома.
| Автор | |
|---|---|
| Дата добавления | 28.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 7922 |
| Номер материала | 380 |