
Урок "Упрощение выражений"

Краткое описание документа:
Видеоурок «Упрощение выражений» раскрывает некоторые возможности операций при выполнении преобразования выражений. В ходе видеоурока на примерах подробно раскрывается суть распределительного свойства умножения, а также сочетательного свойства, приводится много примеров, помогающих усвоить материал. С помощью видеоурока учитель имеет возможность наглядно, понятно для учеников представить материал. При этом ему не нужны другие пособия, чтобы сформировать понятие. С помощью видеоурока можно быстрее достичь целей урока, повысить его эффективность.
При составлении видео были использованы инструменты, которые воздействуют на мыслительные процессы ученика, стимулируя запоминание и понимание материала. Представление текста в цвете помогает быстрее его запомнить, выделить важные понятия, формируя понимание. С помощью анимационных эффектов достигается последовательное изложение материала, возможность подчеркнуть важные особенности в решении задач, сделать решения более наглядными. С помощью иллюстраций легче наглядно представить изучаемый материал. Так как видео озвучено, это позволяет дополнить его комментариями учителя, которые помогают лучше усвоить материал.
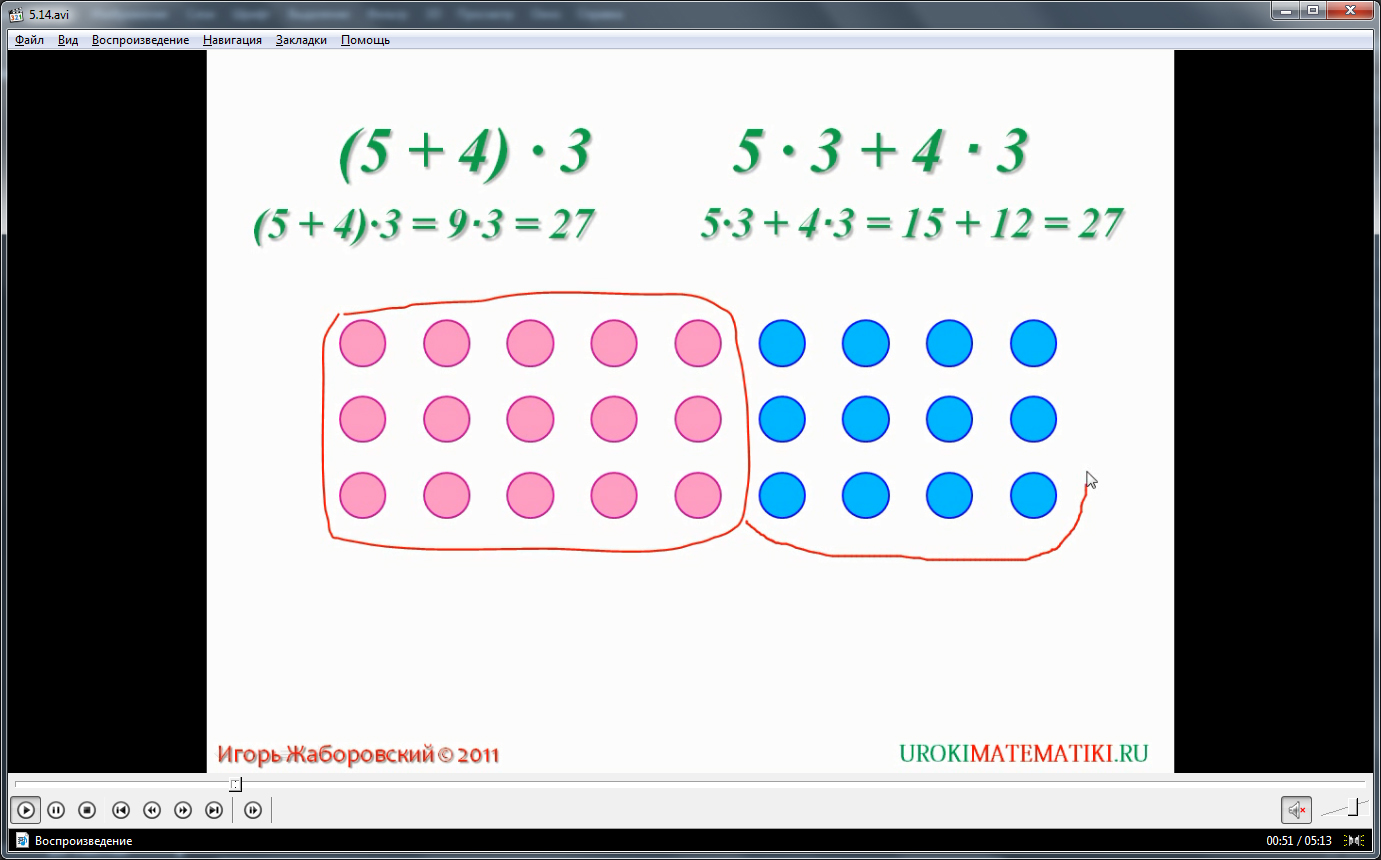
Видеоурок начинается с представление его темы. На экране отображается два выражения (5+4)·3 и 5·3+4·3. Отмечается, что два данных выражения имеют одинаковые ответы. Ниже раскрывается решение данных выражений. Отмечается, что в первом примере при решении выражения в скобках получается 9, которое при умножении на 3 дает 27. Аналогично во втором примере, следуем правилам выполнения операций. При умножении 5 на 3 получается 15, а при умножении 4·3 получается 12. Сложив между собой 12 и15, также можно получить 27.
Объяснение равенства выражений выполняется с помощью рисунка. На экране изображены 27 кружков, при этом 5 столбцов в три ряда – розовые кружки и 4 столбца в три ряда – голубые кружки. Для подсчета общего количества кружков можно выделить количество столбцов розовых кружков – 5 и количество столбцов голубых кружков – 4, а с учетом того, что для обоих цветов одинаковое число рядов – 3, составить выражения поиска решения (5+4)·3. Если же подсчитывать количество кружков отдельно для каждого цвета, а затем сложить вместе, то получим сумму произведения 5·3 с произведением 4·3.
Рассмотренный пример обобщается в общем правиле – чтобы перемножить число с некоторой суммой, необходимо умножить на него каждое слагаемое суммы, а после эти произведения сложить. Отмечается, что данное правило представляет распределительное свойство операции умножения. Формулировка правила, название свойства выделены цветным шрифтом и могут быть рекомендованы учителем к запоминанию. Далее следует буквенное обозначение распределительного свойства (a+b)c=ac+bc.
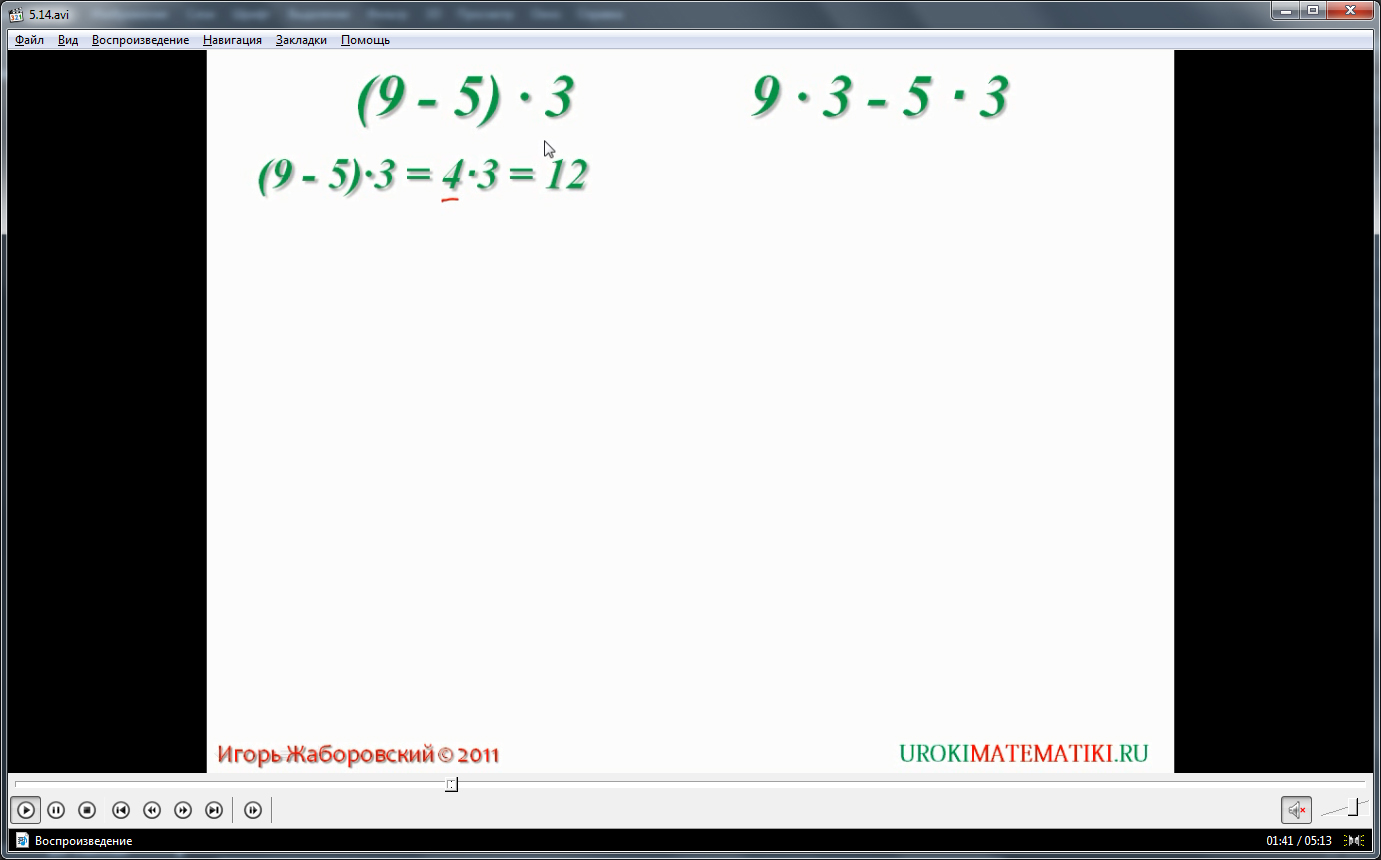
Далее представляется распределительное свойство, когда выражение в скобках представляет собой разность. Сравниваются решение выражения (9-5)·3 с решением 9·3-5·3. Отмечается, что данные выражения также имеют одинаковые значения. При вычислении разности в скобках 9-5 получается 4, то при умножении его на 3 получается 12. Аналогично при решении второго выражения получаем из первого произведения 9·3 значение 27, а из второго произведения получаем 15. Значение в результате вычитания из 27 числа 15 получаем 12. Таким образом, значения выражений равны. Отмечается, что данный пример является подтверждением распределительного свойства операции умножения, выполняемого относительно вычитания. Само свойство в общем виде указано в текстовом виде ниже примера. Сообщается, что для умножения разности чисел на третье число необходимо умножить на него уменьшаемое, а также вычитаемое, после этого от первого найденного произведения следует отнять второе произведение. Название правила выделено цветным шрифтом. Ниже текстового представления свойства дается буквенное его представление.
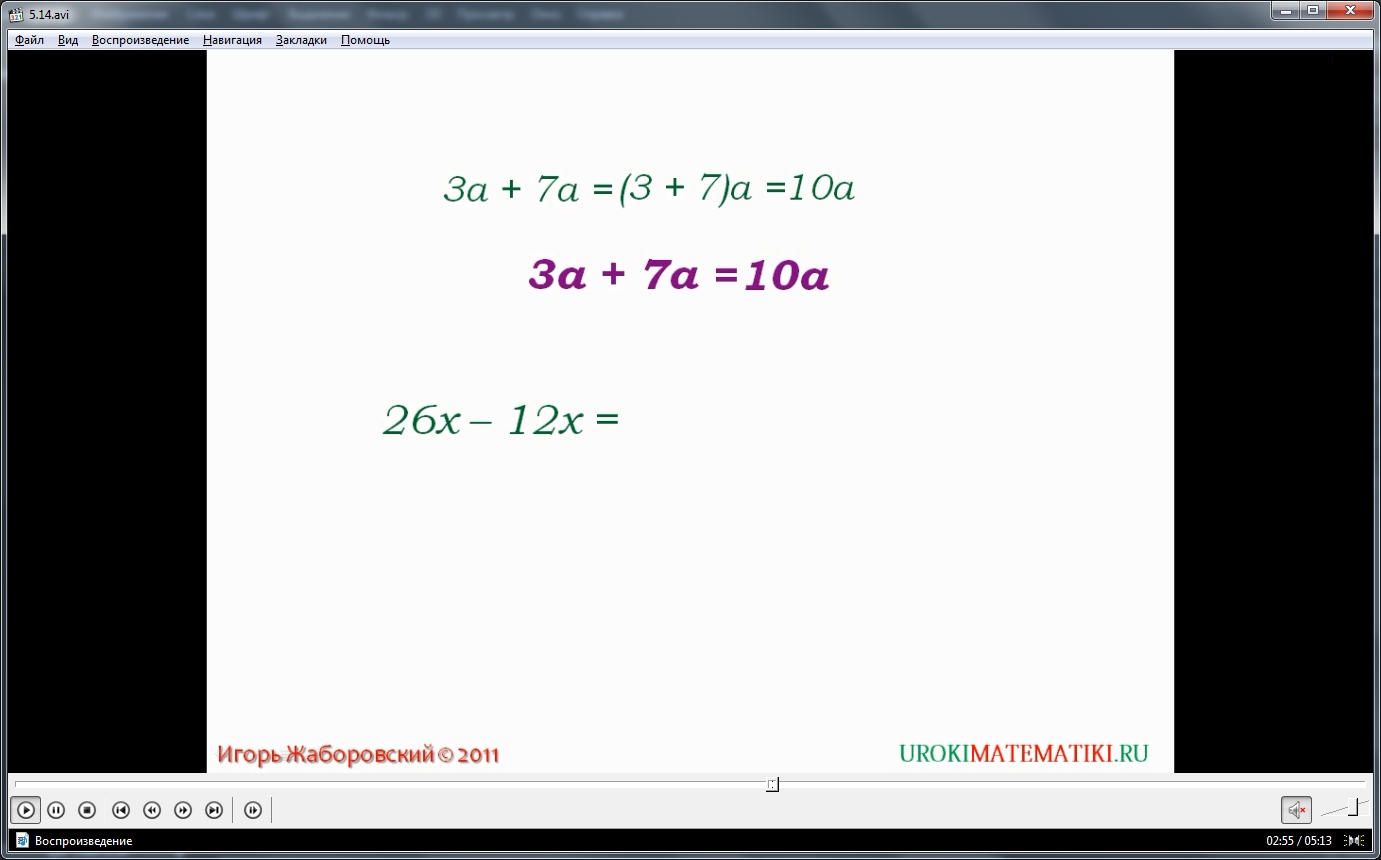
Отмечается, что рассмотренные свойства помогают в упрощении выражений. Представляются примеры, которые можно упростить помощью данного свойства. Используя данное свойство, упрощается 3а+7а. Так как выражение представляет собой сумму произведений, в каждом из которых есть множитель а, сначала в скобки заносится сумма числовых коэффициентов (3+7), а затем это выражение умножается на а. Выражение в скобках можно вычислить, в результате чего получается выражение 10а. Указывается краткая запись вычисления. Оговаривается, что обычно опускается вынесение общего множителя за скобки, записывая 3а+7а=10а. Чтобы объяснить, как получается данное выражение, дается наглядный образ – вместо х предлагается представить конфету. Таким образом, складывая 3 конфеты и 7 конфет, получается 10 конфет.
Таким же образом выполняется упрощение выражения 26х-12х. Сначала в скобки заносится выражение (26-12), а затем умножается на общий множитель х. в результате вычисления выражения в скобках, получаем значение выражения 14х. Так же, как и в предыдущем примере, оговаривается краткая запись упрощения 26х-12х=14х. пример также дополнен наглядным образом, предлагая представить вместо х конфеты. Таким образом, если вычесть из 26 конфет 12 конфет, то получится 14 конфет.
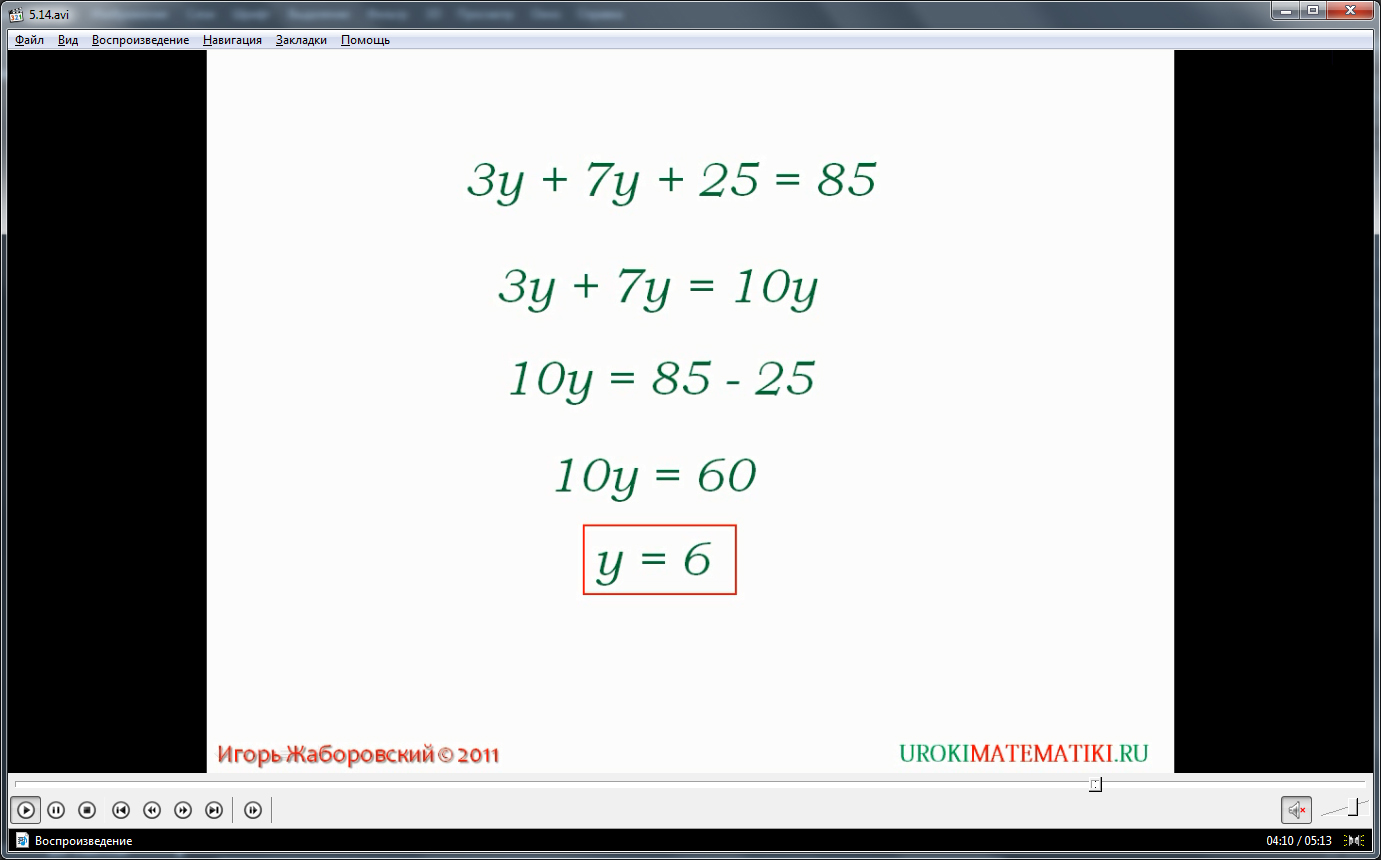
Далее предлагается рассмотреть решение уравнения 3у+7у+25=85. Учитывая возможность упростить уравнение, так как в нем есть выражение 3у+7у, то оно принимает вид 10у+25=85. Чтобы найти 10у, нужно из 85 вычесть 25. В результате получаем упрощенное уравнение 10у=60. Делением 60 на 10 получаем ответ у=6. Справедливость решения проверяем подстановкой 6 вместо у в исходное уравнение 3·6+7·6+25=85. Так как после вычисления выражения в левой части получаем число 85, уравнение решили верно.
Далее рассматривается сочетательное свойство умножения. Предлагается рассмотреть пример 2у·7·10. Чтобы решить данный пример, можно перераспределить множители так, чтобы у остался за скобками (2·7·10)у. после вычисления выражения в скобках, получаем 140у.
В конце видеоурока предлагается ответить на вопросы для проверки, насколько усвоен учебный материал. На первый вопрос необходимо ответить, как формулируется распределительное свойство операции умножения, выполняемого относительно вычитания, сложения. Во втором вопросе следует пояснить с помощью изученных правил упрощение выражений.
Видеоурок «Упрощение выражений» используется на традиционном школьном уроке математики для повышения его эффективности. Также он может использоваться учителем, осуществляющим дистанционное обучение, в качестве наглядного пособия. Материал может быть рекомендован ученикам, которым необходимо дополнительное занятие для усвоения материала, или требуется самостоятельное изучение на дому.
| Автор | |
|---|---|
| Дата добавления | 28.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 6577 |
| Номер материала | 376 |