
Урок «Площадь поверхности цилиндра»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Поверхность цилиндра состоит из боковой поверхности, и оснований цилиндра, которые представляют собой два круга.
Длина образующей боковой поверхности называется высотой цилиндра (АВ), а радиус основания - радиусом цилиндра.
Попробуем разрезать боковую поверхность нашего цилиндра по образующей АВ так, чтобы все образующие оказались в плоскости α.
В результате в плоскости α получился прямоугольник ABCD. Этот прямоугольник представляет собой развертку боковой поверхности цилиндра.
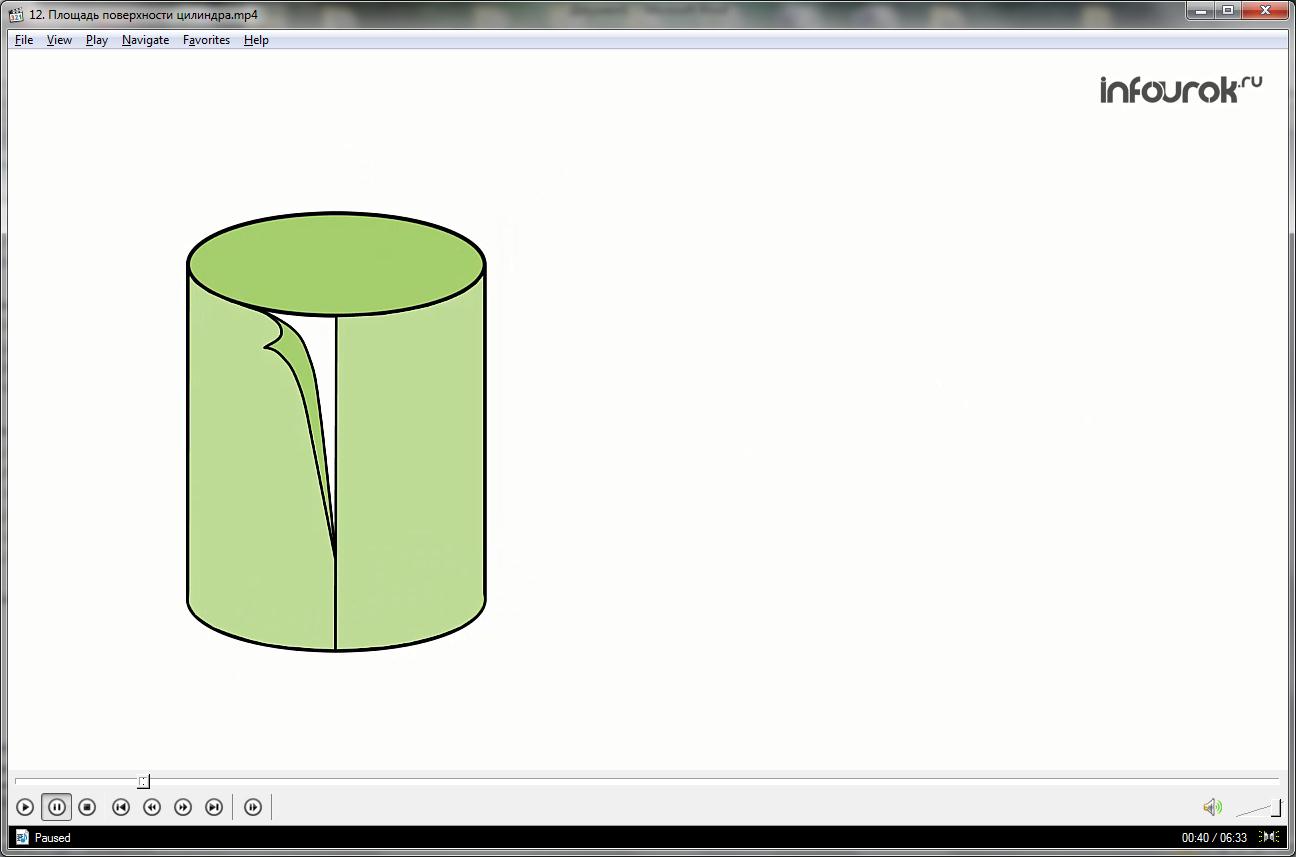
Сторона AD – развертка окружности основания цилиндра, а высота АВ — образующей цилиндра.
Значит, мы получаем:
АВ=h,
AD= (формула длины окружности)
где r — радиус окружности, h — высота цилиндра.
За площадь боковой поверхности цилиндра принимается площадь ее развертки, т.е. площадь прямоугольника АВСD.
Вспомним!
Площадь прямоугольника находится по формуле:
SABCD=АВ•AD
Поэтому, мы получаем:
Sбок = h
площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.
Найдем площадь полной поверхности цилиндра.
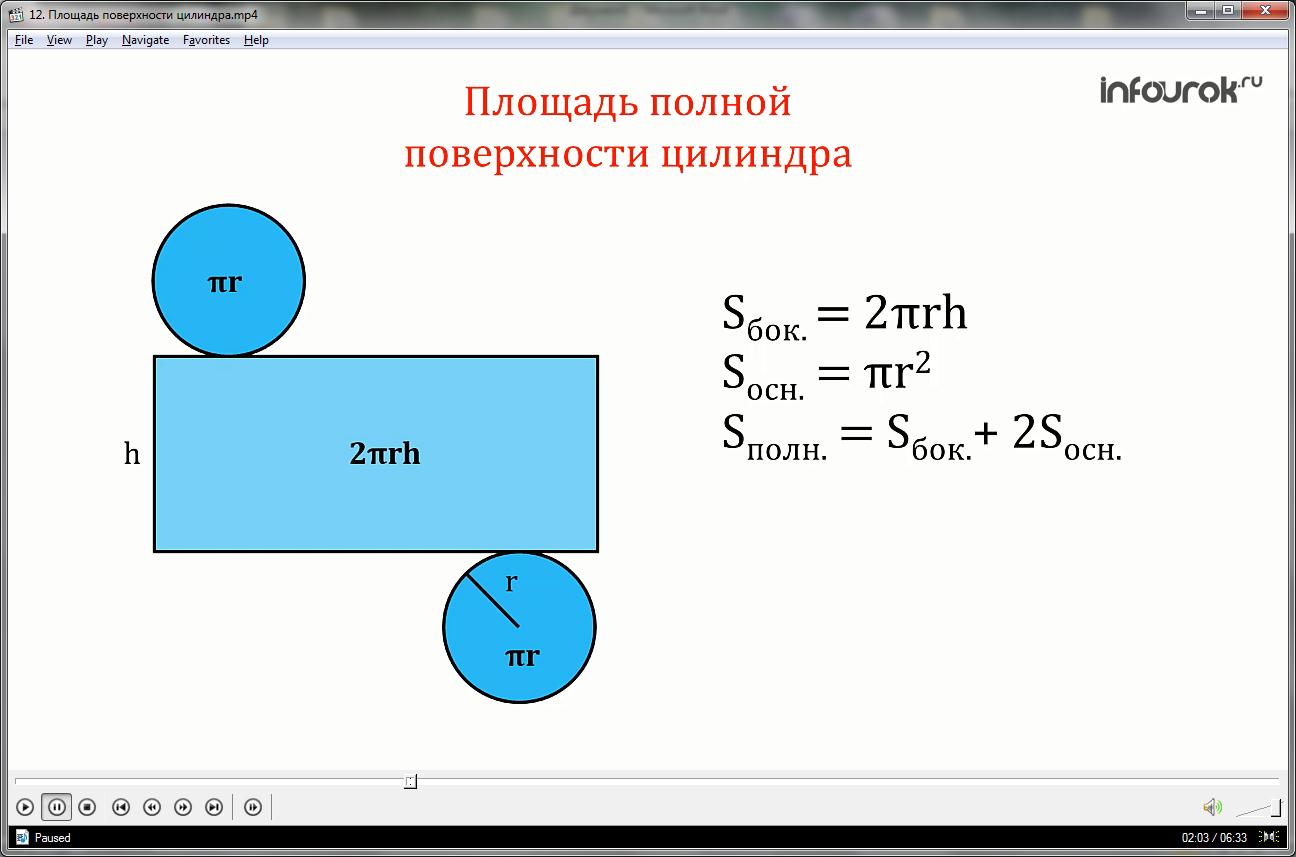
Цилиндр состоит из боковой поверхности и двух оснований.
Площадь полной поверхности цилиндра равна сумме площади двух оснований и боковой поверхности.
Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:
Sбок.=2πrh
Sосн.= πr2,
Sполн. =Sбок.+2Sосн.
Sполн. = 2πr(h + r)
Полученные знания применим при решении задач.
Задача 1.
Трубка цилиндрической формы получается из прямоугольника. Вычислите радиус основания, если длина прямоугольника равна 16 см, ширина – 12см.
Решение:
Так как трубка получается из прямоугольника, то его длинна – это есть длина окружности.
Формула длины окружности:
С = 2πr
Значит, C=ВС=16 см,
Найдем радиус окружности: (отношение длины окружности к двум пи)
r = = = см
Задача 2.
Дано: цилиндр, ABCD-осевое сечение, АС=48 см, ACD= 60º.
Найти: а) СD — высота, б) АО — радиус, в) Sосн.
Решение.
а)1.Рассмотрим осевое сечение АВСD.
ABCD — прямоугольник (по условию), значит <ADС=90⁰ .

2. Рассмотрим ∆ ADС:
ACD= 60°(по условию),
ADС=90º(п.1),
тогда СAD=30º
АС — гипотенуза, СD — катет, лежащий против угла в 30⁰.
Он равен половине гипотенузы
СD=АС:2=48:2=24 см.
б) Найдем АО.
АО – радиус основания цилиндра.
АD – диаметр основания цилиндра. Поэтому, найдем диаметр по формуле
АD=
Значит, АО=12 √3 см
в) Найдем Sосн.
И в заключении!
А знаете ли Вы, что……
У отдельных изваяний, оставленных нам древнеегипетской культурой, можно видеть зажатые в руках объекты цилиндрической формы, предназначение которых историкам непонятно.
В 1976 году в Закавказье обнаружена старинная рукопись «Тайны Жизни и Смерти», в которой содержалась информация о Лунном и Солнечном цилиндрах, изготовленных из цинка и меди с определенным внутренним наполнением.
Было установлено, что цилиндры Фараона, так они называются, обладают широчайшим спектром благотворного воздействия на организм человека.
В него входят: помощь при сердечно-сосудистых заболеваниях, нейротрофических, гипертонии, болезнях выводящих путей, астме, бессоннице, головных болях, а также в качестве средства для снятия стрессов и профилактики атеросклероза.
Согласно мнению ряда врачей, Цилиндры Фараона представляют собой уникальный, самонастраивающийся на каждого человека, физиотерапевтический прибор, созданный гением древнеегипетских ученых.
Исследования показали, что воздействие Цилиндров Фараона переводит организм в иное, более «высокое» энергетическое состояние, при котором активнее протекают восстановительные процессы, способствующие гармонизации всего организма.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 19698 |
| Номер материала | 998 |