
Урок «Понятие цилиндра»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Введем понятие цилиндра – геометрического тела.
Ну конечно, все вы видели много предметов в быту, похожих на данное тело.
Рассмотрим окружность Р с центром О и радиусом r в плоскости α .Через каждую точку окружности проведем прямые, перпендикулярные к плоскости α. Они параллельны друг другу.

Все прямые образуют поверхность, которая называется цилиндрической.
Каждая из этих прямых называется образующей цилиндрическую поверхность, а прямая, проходящая через центр окружности, – осью цилиндрической поверхности.
Далее проведем плоскость сигма, параллельную плоскости альфа, таким образом, что они отделят отрезки образующих, которые равны и параллельны между собой.
В плоскости сигма получим окружность Р1 .
Ось цилиндрической поверхности пройдет через центр О1 окружности Р1, радиус окружностей будет равный r. Таким образом, мы получили цилиндр.
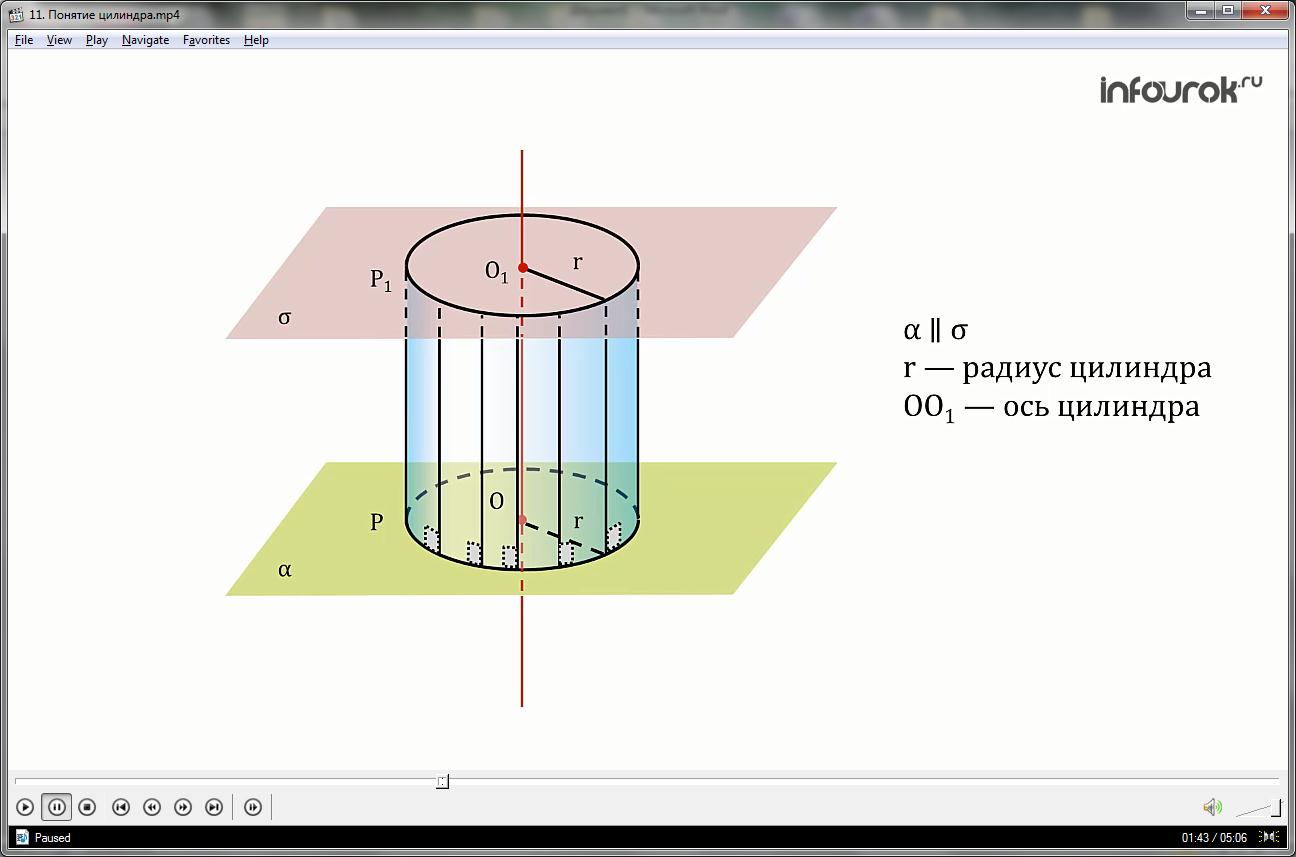
Цилиндром называется тело, ограниченное цилиндрической поверхностью и двумя кругами, лежащими в параллельных плоскостях.
Ось ОО1 – называют осью цилиндра, отрезок образующей цилиндрической поверхности ТТ1– образующая цилиндра.
Цилиндрическая поверхность, т.е. поверхность, составленная из образующих, называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон. На рисунке изображен цилиндр, полученный вращением прямоугольника вокруг стороны ОО1.
Рассмотрим сечение цилиндра.
1) Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.
2) Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.
Теперь давайте посмотрим, какие бывают цилиндры.

1) Прямые и наклонные, в зависимости от того, перпендикулярны или наклонны плоскости оснований к образующим.
2) Сложные цилиндры.
На первом рисунке
изображён цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы и отрезком.
На втором рисунке изображен цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскости оснований (наклонный цилиндр).
Задача
Докажите, что осевое сечение цилиндра является прямоугольником, две противоположные стороны которого – образующие, а две другие – диаметры оснований цилиндра. Найти диагональ осевого сечения, если радиус цилиндра равен 1,5 м, а высота равна 4 м.
Решение
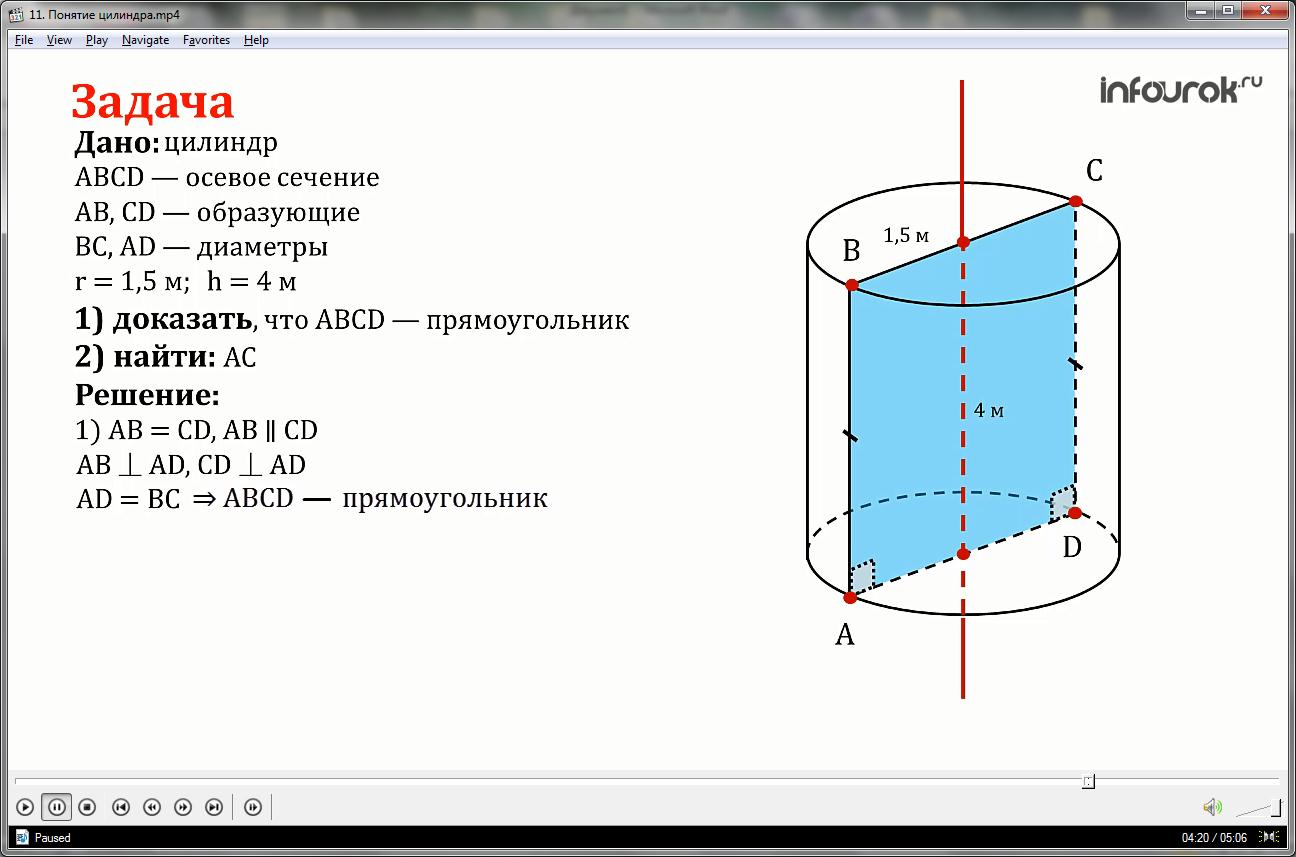
1) так как АВ и CD – образующие то они равны и параллельны, и по определению образующих цилиндра АВ и CD перпендикулярны основанию.
AD и BC равны как диаметры оснований,
следовательно, четырехугольник ABCD по признаку параллелограмма и определению является прямоугольником.
2) Диагональ АС делит прямоугольник на два равных прямоугольных треугольника, тогда,
из прямоугольного треугольника АВС находим АС: по теореме Пифагора АС равна корню квадратному из суммы квадратов сторон АВ и АС, где АВ равна высоте цилиндра, а ВС диаметру основания то есть двум радиусам.
Получаем АС равно 5 м.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 12164 |
| Номер материала | 997 |