
Урок «Понятие конуса»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Сегодня мы рассмотрим пространственную геометрическую фигуру — «круглое» геометрическое тело — конус.
Давайте вспомним, какие предметы, окружающие нас, имеют форму конуса.
Теперь рассмотрим, как строится конус. Сначала изображаем в плоскости α окружность L с центром O и прямую OP, перпендикулярную к этой окружности.

Каждую точку окружности соединим прямыми с точкой P. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности.
Точка Р называется вершиной, а прямая OР – осью конической поверхности.
Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Коническая поверхность называется боковой поверхностью конуса, а круг – основанием конуса.
Прямая OP, проходящая через центр основания и вершину, называется осью конуса.
Ось конуса перпендикулярна плоскости основания.
Отрезок OP называется высотой конуса. Точка P называется вершиной конуса, а образующие конической поверхности – образующими конуса.
Следует запомнить, что все образующие конуса равны друг другу.
Ещё один способ построения конуса – вращением прямоугольного треугольника вокруг одного из его катетов.
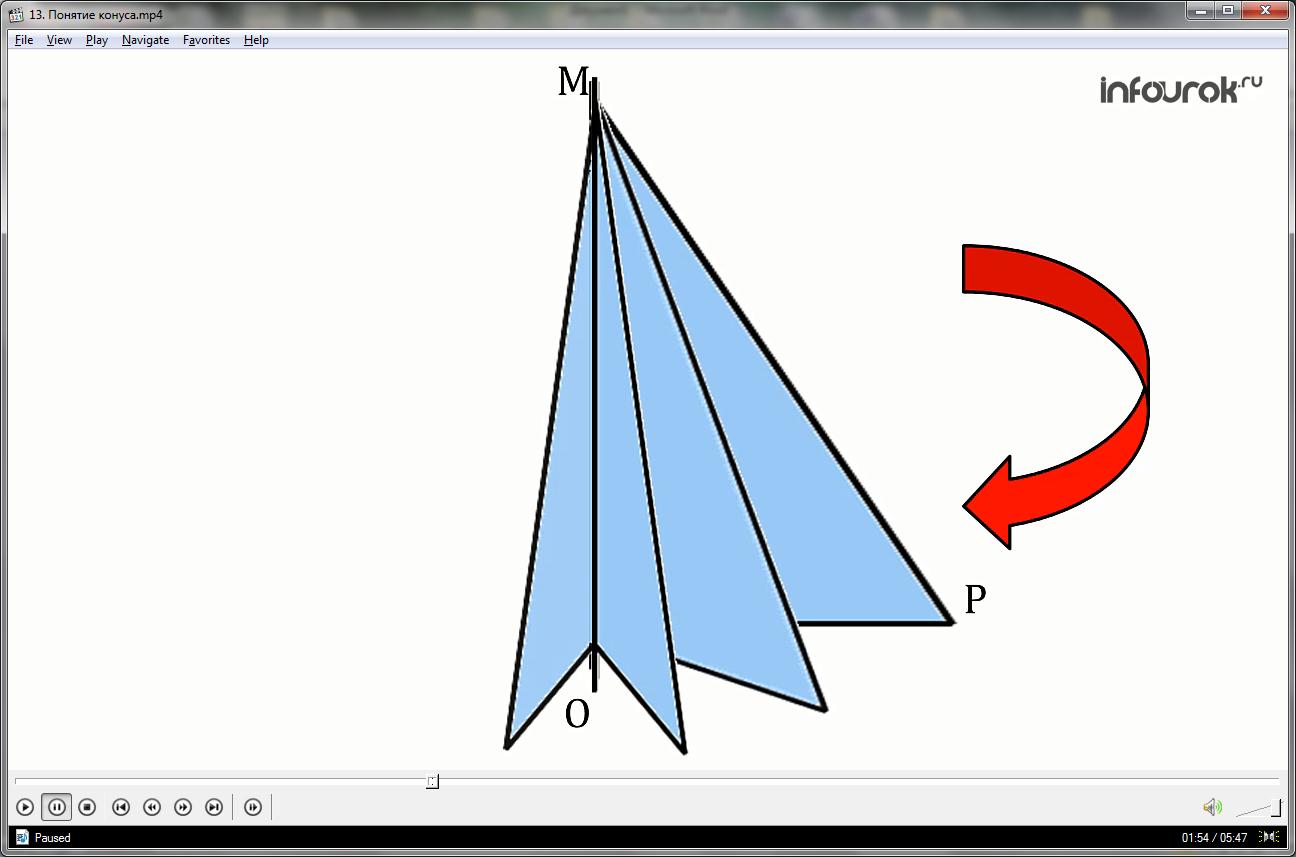
На рисунке изображен конус, полученный вращением прямоугольного треугольника МОР вокруг катета МО. При этом боковая поверхность конуса образуется вращением гипотенузы МР, а основание — вращением катета РО.
Рассмотрим сечение конуса различными плоскостями.
1.Секущая плоскость проходит через ось конуса.
В этом случае сечение представляет собой равнобедренный треугольник, основание которого — диаметр основания конуса, а боковые стороны — образующие конуса. Это сечение называется осевым.
2.Секущая плоскость перпендикулярна оси ОР конуса.
В этом случае сечение конуса представляет собой круг с центром О, расположенным на оси конуса.
Радиус r1 этого круга равен ,
где r - радиус основания конуса, что легко усмотреть из подобия прямоугольных треугольников РОМ и РО1М1.
Докажем, что треугольники подобны.
У прямоугольного треугольника один угол прямой. Для подобия двух прямоугольных треугольников достаточно, чтобы у них было по равному острому углу. Треугольники РОМ и РО1М1. подобны, так как имеют общий острый угол Р, следовательно, сходственные стороны пропорциональны.
Задача
Высота конуса равна 15 см, а радиус основания равен 8 см. Найдите образующую конуса.
Построим чертеж и запишем, что дано и что найти по условию задачи.
Решение:

Рассмотрим треугольник ОРВ, он прямоугольный, так как РО перпендикулярно АВ и, по определению конуса, — его высота, значит угол РОВ=90⁰.
Из треугольника ОРВ по теореме Пифагора найдем РВ — гипотенузу треугольника и образующую конуса.
Историческая справка!
Коническое сечение есть пересечение плоскости с круговым конусом. Впервые рассмотрел их Аполлоний, который в математике известен своими «Коническими сечениями», в которых он дал полное изложение теории, причем развил аналитические и проективные методы.
Существует три главных типа конических сечений: эллипс, парабола и гипербола.
а) Секущая плоскость пересекает все образующие конической поверхности в точках одной его полости; линия пересечения есть замкнутая овальная кривая — эллипс; окружность как частный случай эллипса получается, когда секущая плоскость перпендикулярна оси конуса.
б) Секущая плоскость параллельна одной из касательных плоскостей конической поверхности; в сечении получается незамкнутая, уходящая в бесконечность кривая — парабола, целиком лежащая на одной полости.

в) Секущая плоскость пересекает обе полости конической поверхности; линия пересечения — гипербола — состоит из двух одинаковых незамкнутых, простирающихся в бесконечность частей (ветвей гиперболы), лежащих на обеих полостях конуса.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6105 |
| Номер материала | 999 |