
Урок "Преобразование выражений, содержащих операцию извлечения квадратного корня"

Краткое описание документа:
Видеоурок «Преобразование выражений, содержащих операцию извлечения квадратного корня» - наглядное пособие, с помощью которого учителю легче сформировать умения и навыки в решении задач, содержащих выражения с квадратным корнем. В ходе урока напоминаются теоретические основы, служащие основанием для проведения операций над числами и переменными, имеющимися в подкоренном выражении, описывается решение множества видов задач, которые могут потребовать умения пользоваться формулами преобразования выражений, содержащих квадратный корень, даются методы избавления от иррациональности в знаменателе дроби.
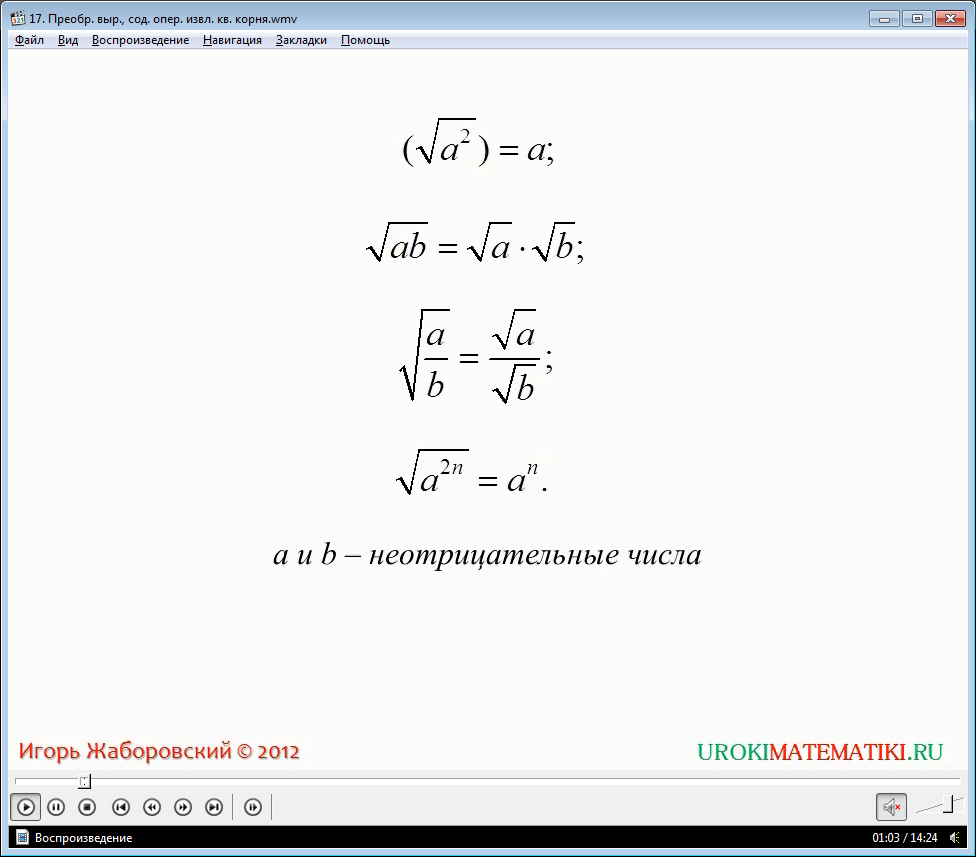
Видеоурок начинается с демонстрации названия темы. Отмечается, что ранее на уроках выполнялись преобразования рациональных выражений. При этом использовались теоретические сведения об одночленах и многочленах, методы работы с многочленами, алгебраическими дробями, а также формулы сокращенного умножения. В данном видеоуроке рассматривается введение операции по извлечению квадратного корня для преобразования выражений. Ученикам напоминаются свойства операции по извлечению квадратного корня. Среди таких свойств указано, что после извлечения квадратного корня из квадрата числа получается само число, корень произведения двух чисел равен произведению двух корней от этих чисел, корень частного двух чисел равен частному корней от членов частного. Последнее рассмотренное свойство – извлечение квадратного корня из числа, возведенного в четную степень √a2n, которое в результате образует число в степени an. Рассмотренные свойства действительны для любых неотрицательных чисел.
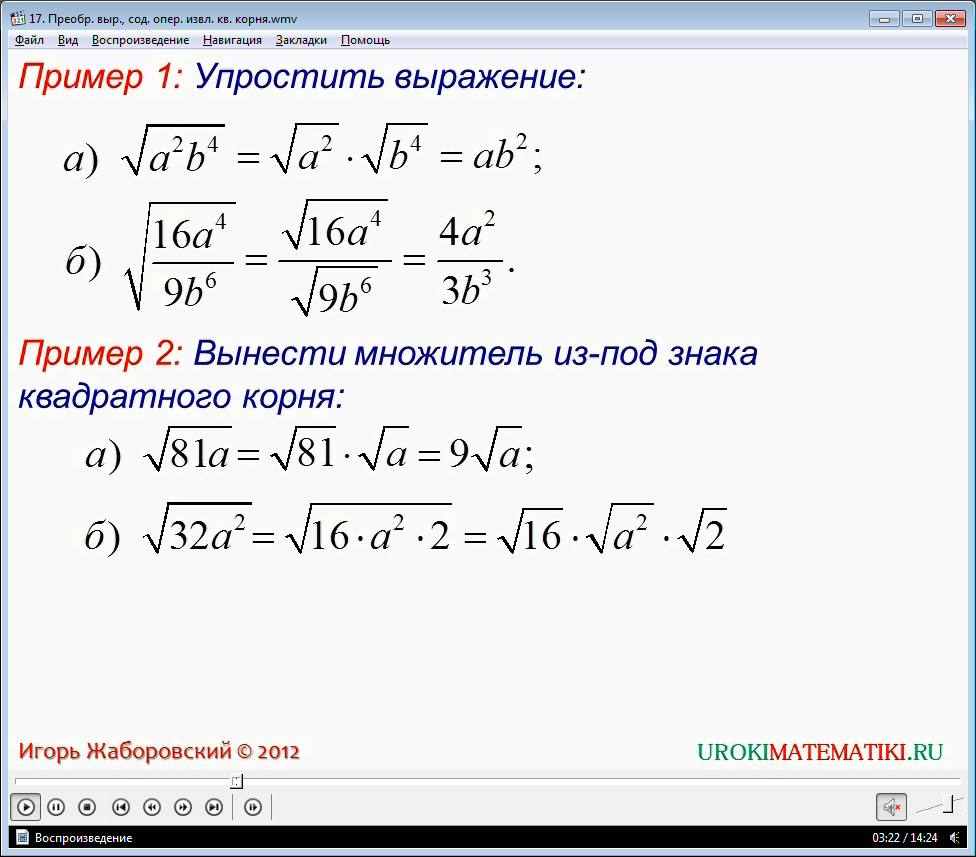
Рассматриваются примеры, в которых требуются преобразования выражений, содержащих квадратный корень. Указано, что в данных примерах предусмотрено, что aи b являются неотрицательными числами. В первом примере необходимо упростить выражения √16a4/9b4 и √a2b4. В первом случае применяется свойство, определяющее, что корень квадратный произведения двух чисел равен произведению корней из них. В результате преобразования получается выражение ab2. Во втором выражении используется формула преобразования квадратного корня частного в частное корней. Итогом преобразования является выражение 4a2/3b3.
Во втором примере необходимо вынести из-под знака квадратного корня множитель. Рассматривается решение выражений √81а, √32а2, √9а7b5. На примере преобразования четырех выражений показывается, как применяется формула преобразования корня произведения нескольких чисел для решения подобных задач. При этом отдельно отмечаются случаи, когда выражения содержат числовые коэффициенты, параметры в четной, нечетной степени. В результате преобразования получаются выражения √81а=9√а, √32а2=4а√2, √9а7b5=3а3b2√ab.
В третьем примере необходимо произвести операцию, противоположную той, что в предыдущей задаче. Для внесения множителя под знак квадратного корня также необходимо уметь пользоваться изученными формулами. Предлагается в выражениях 2√2 и 3a√b/√3a внести множитель перед скобками под знак корня. Используя известные формулы, множитель, стоящий перед знаком корня, возводится в квадрат и помещается в виде множителя в произведение под знаком корня. В первом выражении в результате преобразования получается выражение √8. Во втором выражении сначала применяется формула коня произведения для преобразования числителя, а затем формула корня частного – для преобразования всего выражения. После сокращения числителя и знаменателя в подкоренном выражении, получается √3ab.
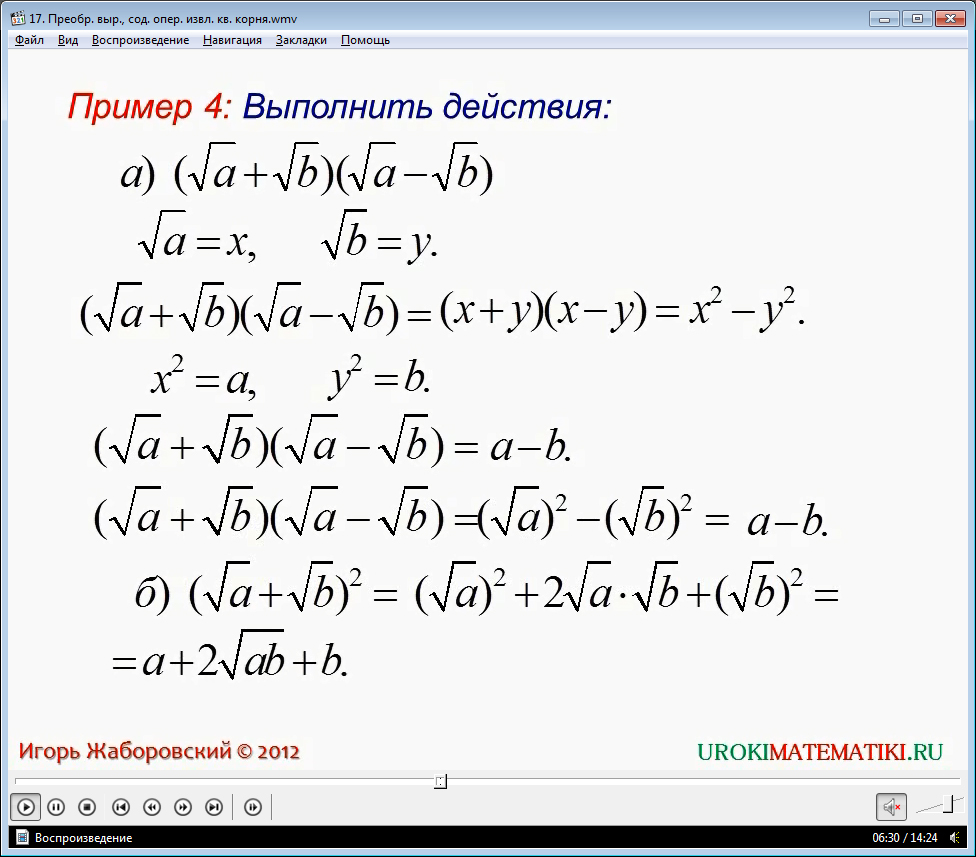
В примере 4 необходимо выполнить действия в выражениях (√a+√b)(√a-√b). Для решения данного выражения вводятся новые переменные, заменяющие одночлены, содержащие знак корня √a=х и √b=у. после подстановки новых переменных, очевидна возможность использования формулы сокращенного умножения, после чего выражение получает вид х2-у2. Возвращаясь к исходным переменным, получаем a-b. Второе выражение (√a+√b)2 также можно преобразовать с помощью формулы сокращенного умножения. После раскрытия скобок получаем результат a+2√ab+b.
В примере 5 производится разложение на множители выражений 4a-4√ab+b и х√х+1. Для решения данной задачи необходимо выполнить преобразования, выделить общие множители. После применения свойств квадратного корня для решения первого выражения сумма преобразуется в квадрат разности (2√а-√b)2. Для решения второго выражения необходимо занести под корень множитель перед знаком корня, а затем применить формулу для суммы кубов. Результатом преобразования становится выражение (√х+1)(х2-√х+1).
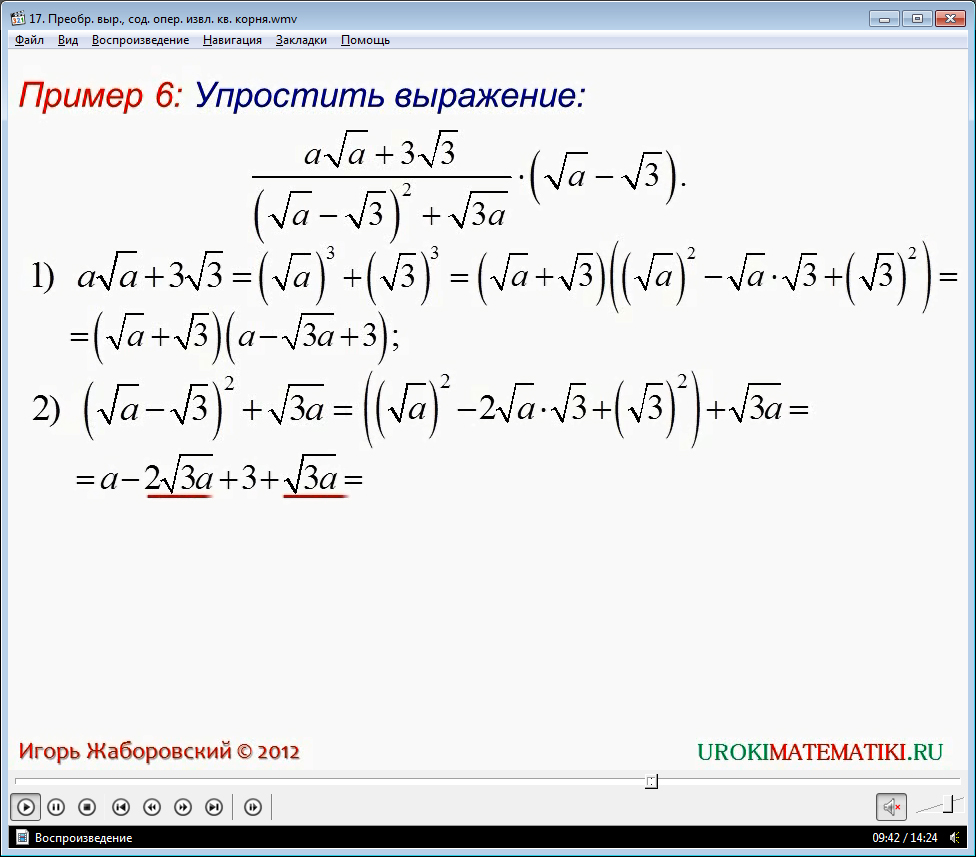
Пример 6 демонстрирует решение задачи, где нужно упростить выражение (а√а+3√3)(√а-√3)/((√а-√3)2+√3а). Решение задания выполняется в четыре действия. В первом действии числитель преобразуется в произведение с помощью формулы сокращенного умножения – суммы кубов двух чисел. Во втором действии преобразуется знаменатель выражения, который получает вид а-√3а+3. После преобразования становится возможным сокращение дроби. В последнем действии применяется также формула сокращенного умножения, которая помогает получить окончательный результат а-3.
В седьмом примере необходимо избавиться от квадратного корня в знаменателях дробей 1/√2 и 1/(√3-√2). При решении задания используется основное свойство дроби. Чтобы избавиться от корня в знаменателе, числитель и знаменатель умножаются на одинаковое число, с помощью которого подкоренное выражение возводится в квадрат. В результате вычислений получаем 1/√2=√2/2 и 1/(√3-√2)=√3+√2.
Указываются особенности математического языка при работе с выражениями, содержащими корень. Отмечается, что содержание квадратного корня в знаменателе дроби означает содержание иррациональности. А об избавлении от знака корня в таком знаменателе говорят как об избавлении от иррациональности в знаменателе. Описываются методы, как можно избавиться от иррациональности – для преобразования знаменателя вида √а необходимо умножить числитель одновременно со знаменателем на число √а, а для устранения иррациональности для знаменателя вида √а-√b, числитель и знаменатель умножаются на сопряженное выражение √а+√b. Отмечается, что избавление от иррациональности в таком знаменателе очень части облегчает решение задачи.
В конце видеоурока рассматривается упрощение выражения 7/√7-2/(√7-√5)+4/(√5+√3). Чтобы упростить выражение, применяются рассмотренные выше способы избавления от иррациональности в знаменателе дробей. Полученные выражения складываются, после чего упрощенный вид выражения имеет вид √5-2√3.
Видеоурок «Преобразование выражений, содержащих операцию извлечения квадратного корня» рекомендуется применять на традиционном школьном уроке для формирования навыков решения заданий, в которых содержится квадратных корень. С этой же целью видео может быть использовано учителем в ходе дистанционного обучения. Также материал может быть рекомендован ученикам для самостоятельной работы дома.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 10800 |
| Номер материала | 541 |