
Урок "Признаки параллельности двух прямых"

Краткое описание документа:
Видеоурок «Признаки параллельности двух прямых» содержит доказательство теорем, которые описывают признаки, означающие параллельность прямых. При этом в видео описывается 1) теорема о параллельности прямых, при которых секущей созданы равные углы, 2) признак, означающий параллельность двух прямых - по равным образованным соответственным углам, 3) признак, означающий параллельность двух прямых в случае, когда при их пересечении секущей односторонние углы в сумме составляют 180°. Задача данного видеоурока – ознакомить учеников с признаками, означающими параллельность двух прямых, знание которых необходимо для решения многих практических задач, наглядно представить доказательство данных теорем, формировать навыки в доказательстве геометрических утверждений.
Преимущества видеоурока связаны с тем, что при помощи анимации, голосового сопровождения, возможности выделения цветом, он обеспечивает высокую степень наглядности, может послужить заменой подачи стандартного блока нового учебного материала учителем.
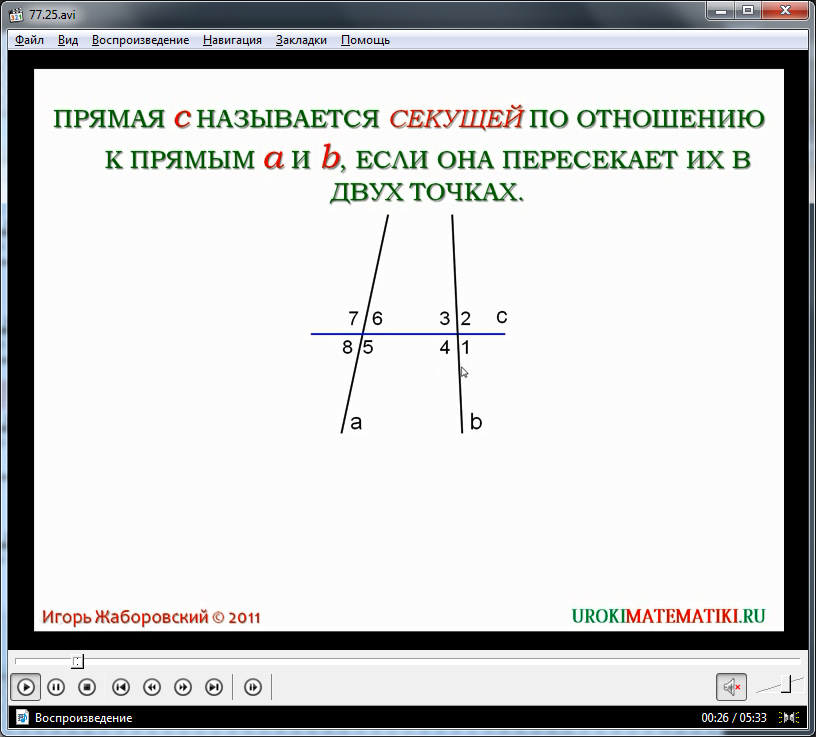
Начинается видеоурок с выведения на экран названия. Перед описанием признаков параллельности прямых ученики знакомятся с понятием секущей. Дается определение секущей как прямой, которая пересекает другие прямые. На экране изображены две прямые a и b, которые пересекаются прямой с. Построенная прямая с выделена синим цветом, акцентируя внимание на том, что они является секущей данных прямых а и b. Для того чтобы рассматривать признаки параллельности прямых необходимо более детально ознакомиться с областью пересечения прямых. Секущая в точках пересечения с прямыми образует 8 углов ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7, ∠8, анализируя соотношения которых можно вывести признаки параллельности данных прямых. Отмечается, что углы ∠3 и ∠5, а также ∠2 и ∠4 называются накрест лежащими. Дается подробное объяснение при помощи анимации расположения накрест лежащих углов как углов, которые лежат между параллельными прямыми, и примыкают к прямым, располагаясь накрест. Затем дается понятие односторонних углов, в число которых входят пары ∠4 и ∠5, а также ∠3 и ∠6. Также указываются пары соответственных углов, которых на построенном изображении 4 пары - ∠1-∠5, ∠4-∠8, ∠2-∠6, ∠3-∠7.
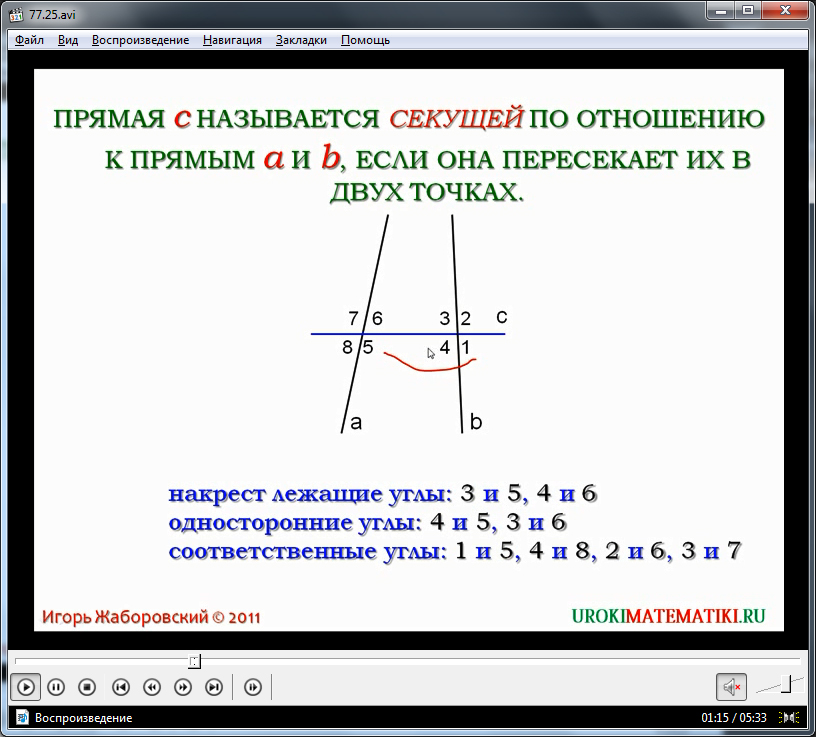
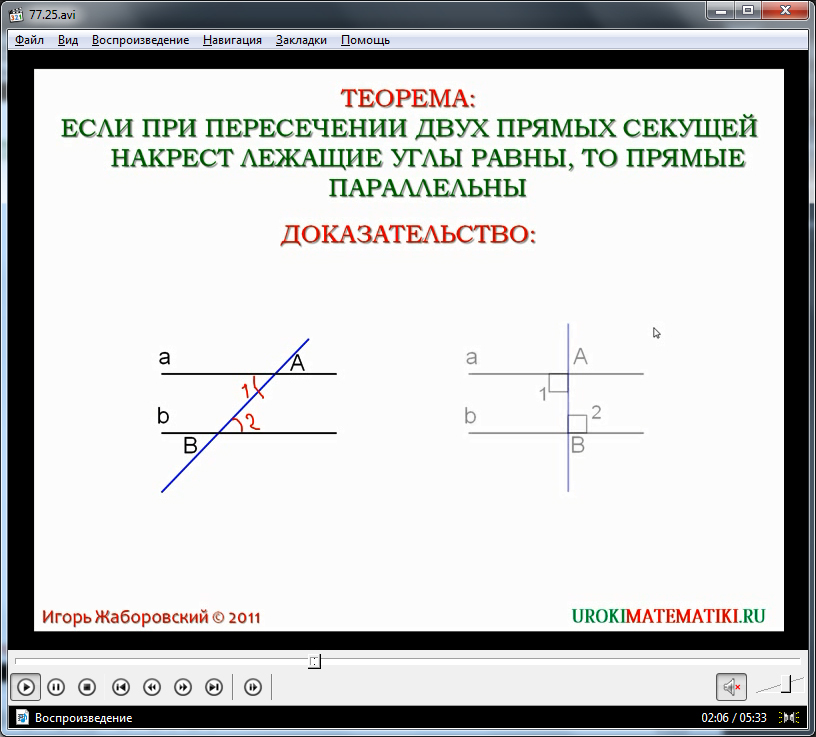
В следующей части видеоурока рассматриваются три признака параллельности любых двух прямых. На экран выводится первое описание. Теорема утверждает, что при равенстве накрест лежащих углов, образуемых секущей, данные прямые будут параллельны. Утверждение сопровождается рисунком, на котором изображены две прямые а и b и секущая АВ. Отмечается, что образуемые накрест лежащие углы ∠1 и ∠2 равны между собой. Данное утверждение требует доказательства.
Наиболее просто доказываемый частный случай – когда данные образуемые накрест лежащие углы являются прямыми. Это означает, что секущая является перпендикуляром к прямым, а по уже доказанной теореме в этом случае прямые а и b не будут пересекаться, то есть являются параллельными. Доказательство для данного частного случая описывается на примере изображения, построенного рядом с первым рисунком, выделяя важные детали доказательства при помощи анимации.
Для доказательства в общем случае необходимо проведение дополнительного перпендикуляра из середины отрезка АВ на прямую а. Далее на прямой b откладывается отрезок ВН1, равный отрезку АН. Из полученной при этом точки Н1 проводится отрезок, соединяющий точки О и Н1. Далее рассматриваются два треугольника ΔОНА и ΔОВН1, равенство которых доказывается по первому признаку равенства двух треугольников. Стороны ОА и ОВ равны по построению, так как точка О отмечалась как середина отрезка АВ. Стороны НА и Н1В также равны по построению, так как мы откладывали отрезок Н1В, равный НА. А углы ∠1=∠2 по условию задачи. Так как образованные треугольники равны между собой, то и соответствующие оставшиеся пары углов и сторон также равны между собой. Из этого следует, что и отрезок ОН1 является продолжением отрезка ОН, составляя один отрезок НН1. При этом отмечается, что так как построенный отрезок ОН – перпендикуляр к прямой а, то соответственно и отрезок НН1 является перпендикулярным к прямым а и b. Данный факт означает, используя теорему о параллельности прямых, к которым построен один перпендикуляр, что данные прямые а и b являются параллельными.
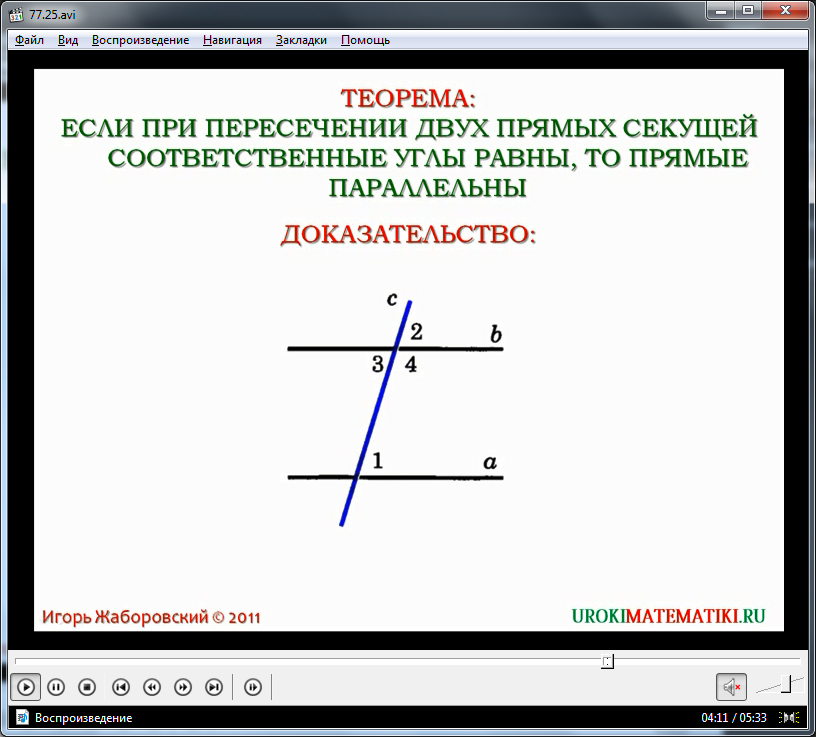
Следующая теорема, требующая доказательства – признак равенства параллельных прямых по равенству соответственных углов, образованных при пересечении секущей. Утверждение указанной теоремы выведено на экран и может быть предложено под запись учениками. Доказательство начинается с построения на экране двух параллельных прямых а и b, к которым построена секущая с. Выделенная на рисунке синим цветом. Секущей образованы соответственные углы ∠1 и ∠2, которые по условию равны между собой. Также отмечаются смежные углы ∠3 и ∠4. ∠2 по отношению к углу ∠3 является вертикальным углом. А вертикальные углы всегда равны. К тому же углы ∠1 и ∠3 являются накрест лежащими между собой – их равенство (по уже доказанному утверждению) означает, что прямые а и b параллельны. Теорема доказана.
Последняя часть видеоурока посвящена доказательству утверждения о том, что если сумма односторонних углов, которые образованы при пересечении двух некоторых прямых секущей прямой, будет равняться 180°, в этом случае данные прямые будут параллельны между собой. Доказательство демонстрируется, используя рисунок, на котором изображены прямые а и b, пересекающиеся с секущей с. Образованные пересечением углы отмечены аналогично предыдущему доказательству. По условию, сумма углов ∠1 и ∠4 равна 180°. При этом известно, что сумма углов ∠3 и ∠4 равна 180°, так как они являются смежными. Это означает, что углы ∠1 и ∠3 равны между собой. Данный вывод дает право утверждать, что прямые а и b параллельны. Теорема доказана.
Видеоурок «Признаки параллельности двух прямых» может быть использован учителем в качестве самостоятельного блока, демонстрирующего доказательства названных теорем, заменяющего объяснение учителя или сопровождающего его. А подробное объяснение дает возможность использовать материал для самостоятельного изучения учениками и поможет в объяснении материала при дистанционном обучении.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 8117 |
| Номер материала | 512 |