
Урок "Пропорциональные отрезки в прямоугольном треугольнике"

Краткое описание документа:
Сегодня вашему вниманию предлагается еще одна презентация по удивительному и загадочному предмету – геометрии. В этой презентации мы вас познакомим со новым свойством геометрических фигур, в частности, с понятием пропорциональных отрезков в прямоугольных треугольниках.
Для начала следует вспомнить, что же такое треугольник? Это простейший многоугольник, состоящий из трех вершин, соединенных тремя отрезками. Прямоугольным называют треугольник, у которого один из углов равняется 90 градусам. Более подробно с ними вы уже знакомились в наших предыдущих учебных материалах, представленных вашему вниманию.
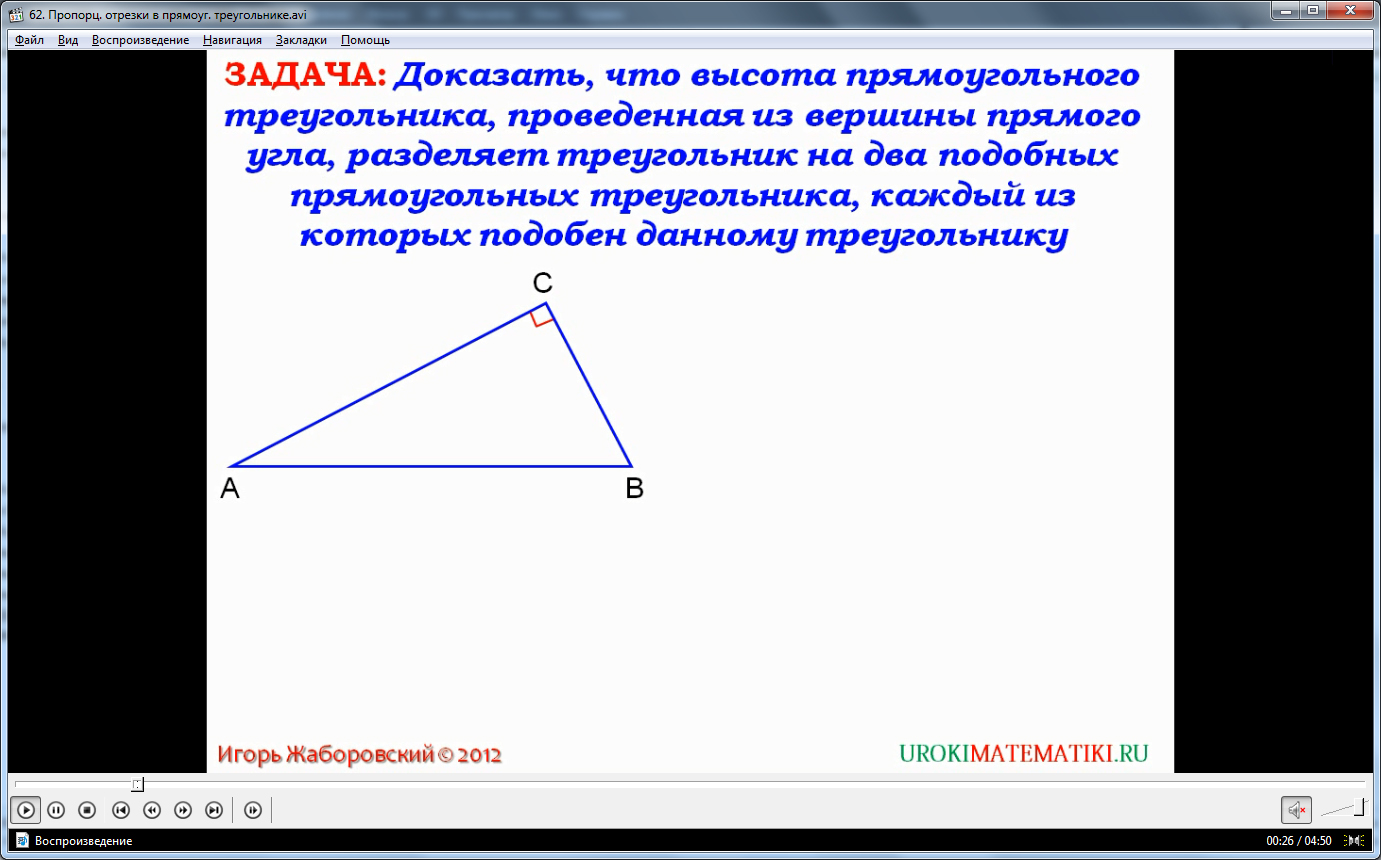
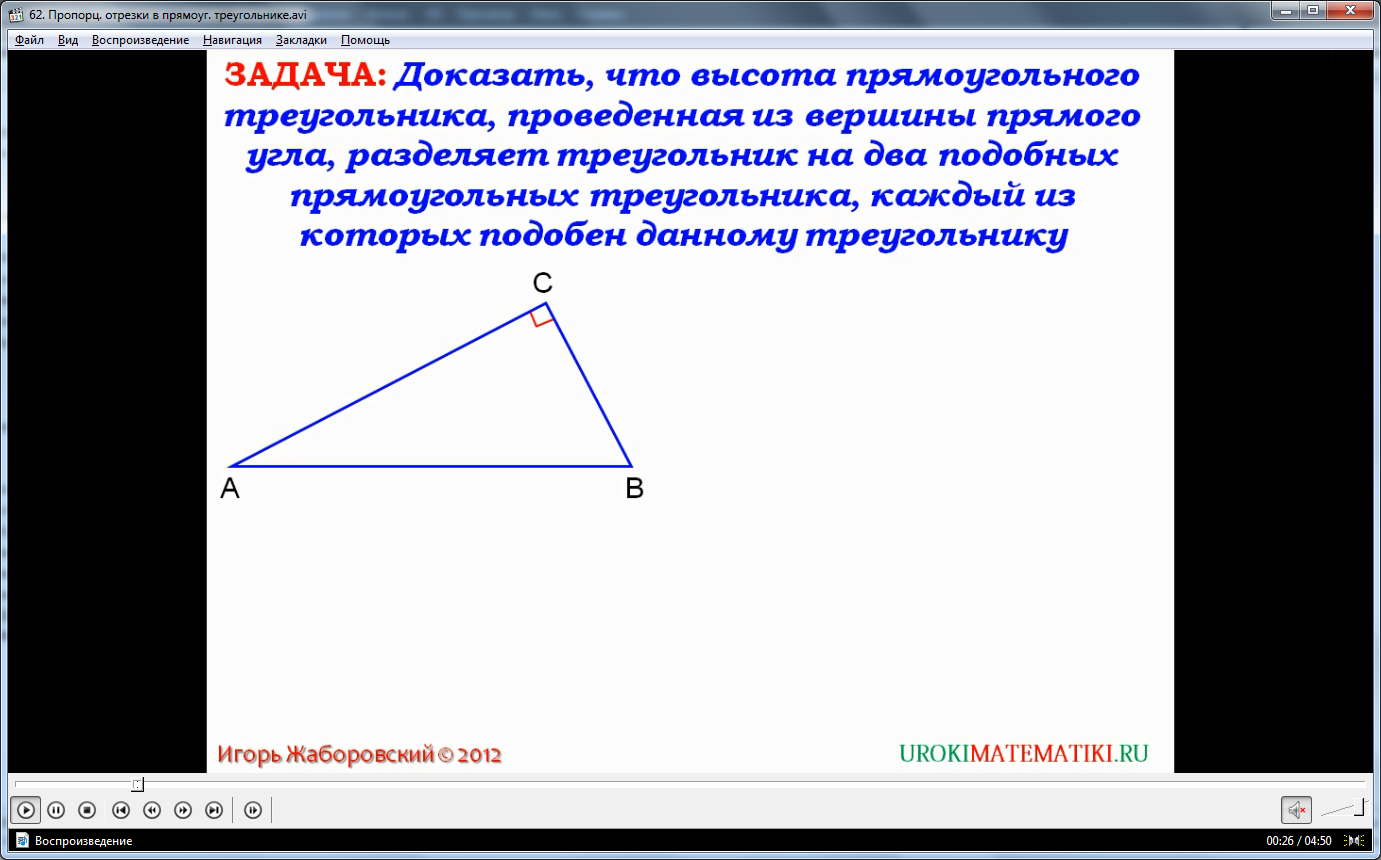
Итак, возвращаясь к нашей сегодняшней теме, по порядку обозначим, что высота прямоугольного треугольника, проведенная из угла 90 градусов, делит его на два треугольника, которые подобны как между собой, так и с исходным. Все интересующие вас рисунки и графики приведены в предложенной презентации, к ним и рекомендуем обращаться, сопровождая описываемым объяснением.
Графический пример вышеописанного тезиса можно увидеть на втором слайде. Исходя из первого признака подобия треугольников, треугольники подобны, так как имеют два одинаковых угла. Если указать более подробно, то высота, опущенная на гипотенузу, образует с ней прямой угол, то есть уже есть одинаковые углы, также каждый из образованных углов имеет и исходным по одному общему углу. Итог – два угла, равных друг другу. То есть треугольники подобны.
Также обозначим, что же под собой подразумевает понятие «среднее пропорциональное» или «среднее геометрическое»? Это некий отрезок XY для отрезков AB и CD, когда он равняется квадратному корню произведения их длин.
Из чего также вытекает, что катет прямоугольного треугольника является средним геометрическим между гипотенузой и проекцией этого катета на гипотенузу, то есть другого катета.

Еще одним из свойств прямого треугольника является то, что его высота, проведенная из угла 90о, является средним пропорциональным между проекциями катетов на гипотенузу. Если вы обратитесь к, предложенной вашему вниманию, презентации и другим материалам, то увидите, что там приведено доказательство указанного тезиса в очень простой и доступной форме. Ранее мы уже доказали, что полученные треугольники подобны между собой и с исходным треугольником. Затем, используя соотношение катетов данных геометрических фигур, приходим к тому, что высота прямоугольного треугольника прямо пропорциональна квадратному корню произведения отрезков, которые образовались в результате опущения высоты с прямого угла исходного треугольника.

Последним в презентации указано то, что катет прямоугольного треугольника является средним геометрическим для гипотенузы и ее отрезка, находящегося между катетом и высотой, проведенной из угла, равного 90 градусам. Этот случай следует рассматривать с той стороны, что указанные треугольники подобны между собой, и катет одного из них получается гипотенузой другого. Но более подробно вы с этим познакомитесь, изучив предложенные материалы.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6232 |
| Номер материала | 600 |