
Урок «Сфера и шар»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
В курсе планиметрии вы познакомились с понятием окружности и круга.
Вспомним, что окружность — это множество точек плоскости, расположенных на заданном расстоянии от данной точки (центр окружности).
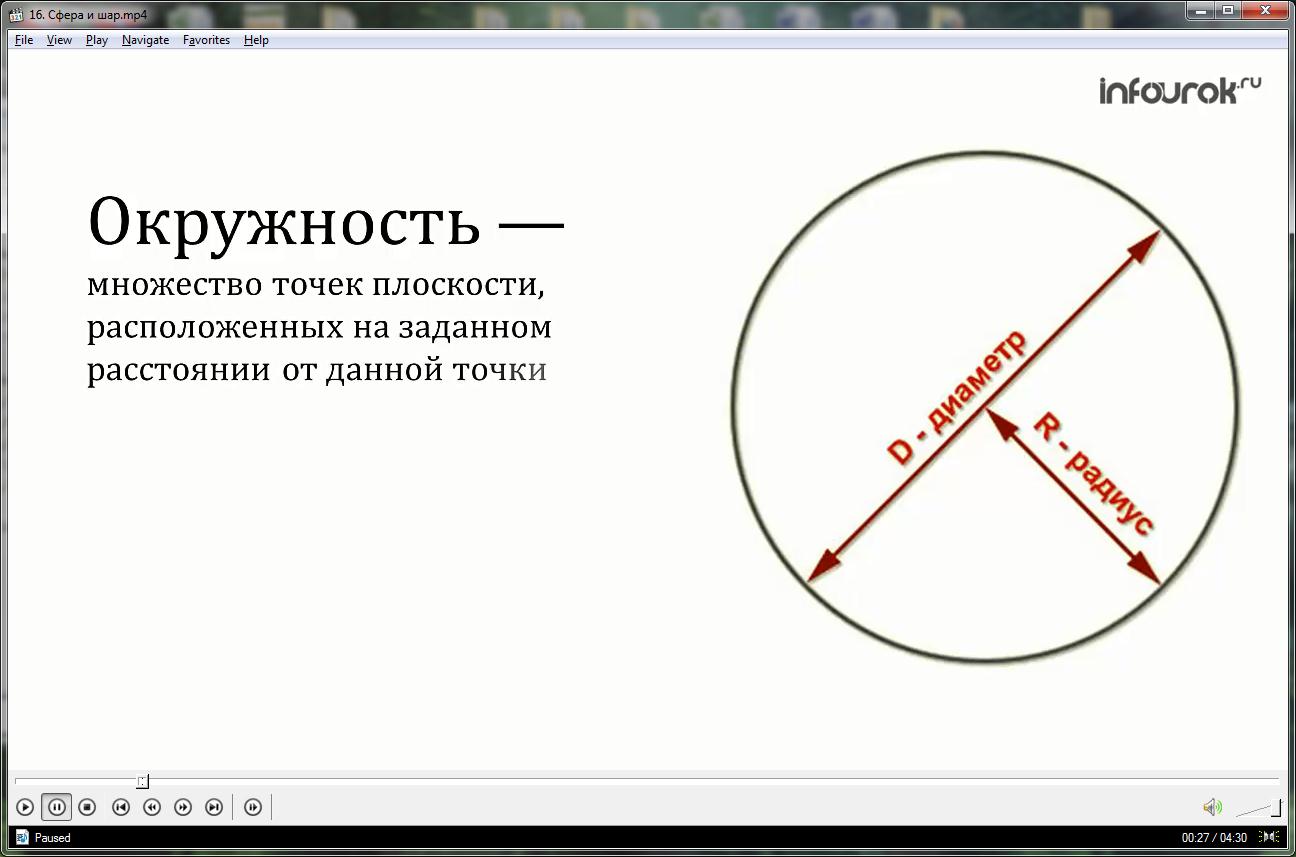
Кругом называется часть плоскости, ограниченная окружностью.
Аналогично понятию окружности на плоскости вводится понятие сферы в пространстве.
Поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, называется сферой.
Данная точка — центр сферы (на рисунке точка О).
Данное расстояние — радиус сферы (на рисунке — отрезок ОС).
Радиусом сферы также называют отрезок, соединяющий центр окружности с любой точкой сферы.
Диаметром сферы называют отрезок, проходящий через центр и любые две точки сферы (на рисунке — отрезок DC).
Аналогично диаметру окружности, диаметр сферы равен двум радиусам.
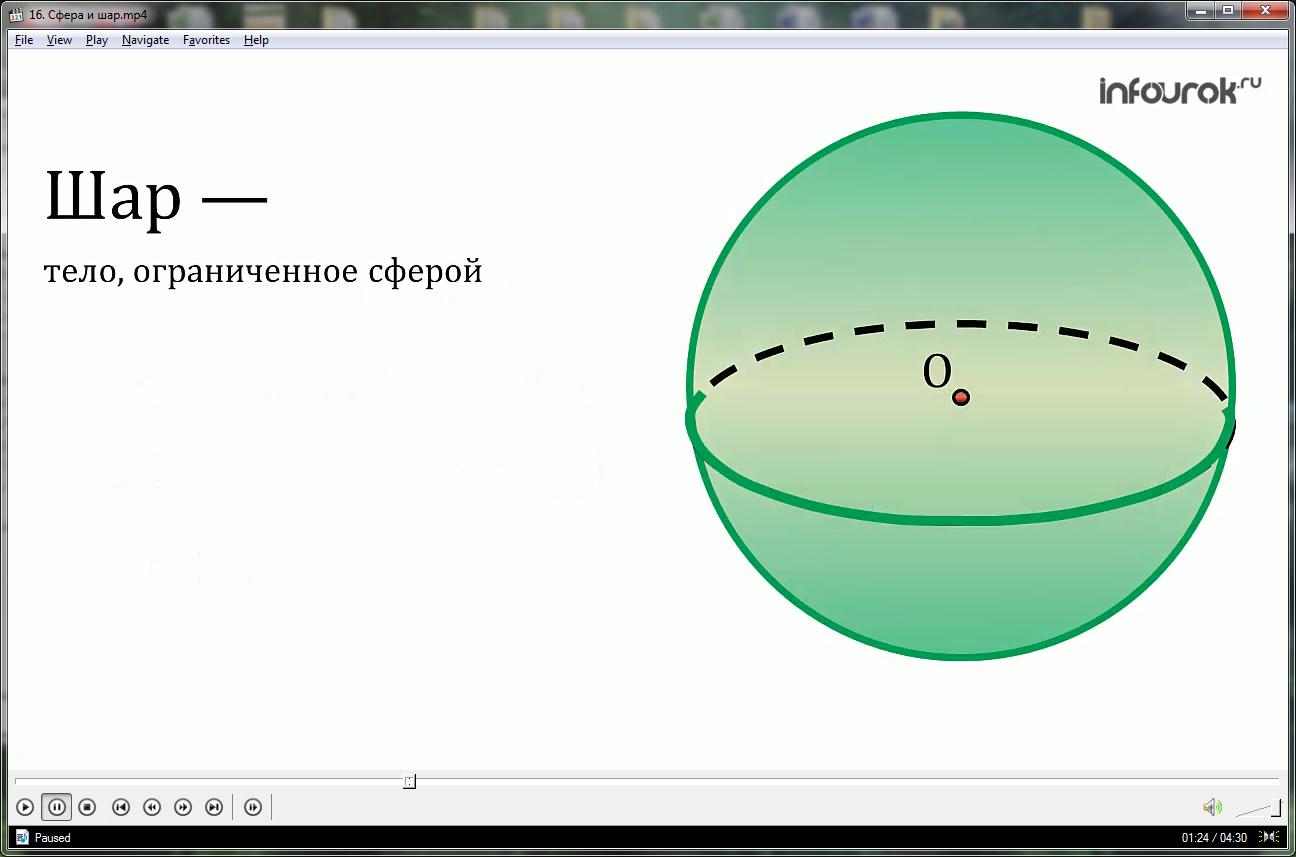
Шаром называется тело, ограниченное сферой.
Существует и другое определение шара — шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.
Очевидно, что центр, радиус, диаметр сферы являются центром, радиусом, диаметром шара.
Сфера может быть получена вращением полуокружности вокруг её диаметра, а шар — вращением полукруга вокруг его диаметра.
Разберём несколько задач, применяя полученные знания.
Задача 1.
Точки А и В лежат на сфере с центром О, О не лежит на отрезке АВ. Доказать, что если М — середина отрезка АВ, то ОМ┴АВ.
Доказательство:
1.АО=ОВ как радиусы, АМ=МВ — по условию, тогда треугольник АОВ – равнобедренный.
2.Отрезок ОМ — медиана треугольника АОВ.

В равнобедренном треугольнике медиана, проведённая к основанию, является высотой, поэтому ОМ┴АВ.
Таким образом, мы доказали, что если М — середина отрезка АВ, то ОМ┴АВ.
Что и требовалось доказать.
Задача 2.
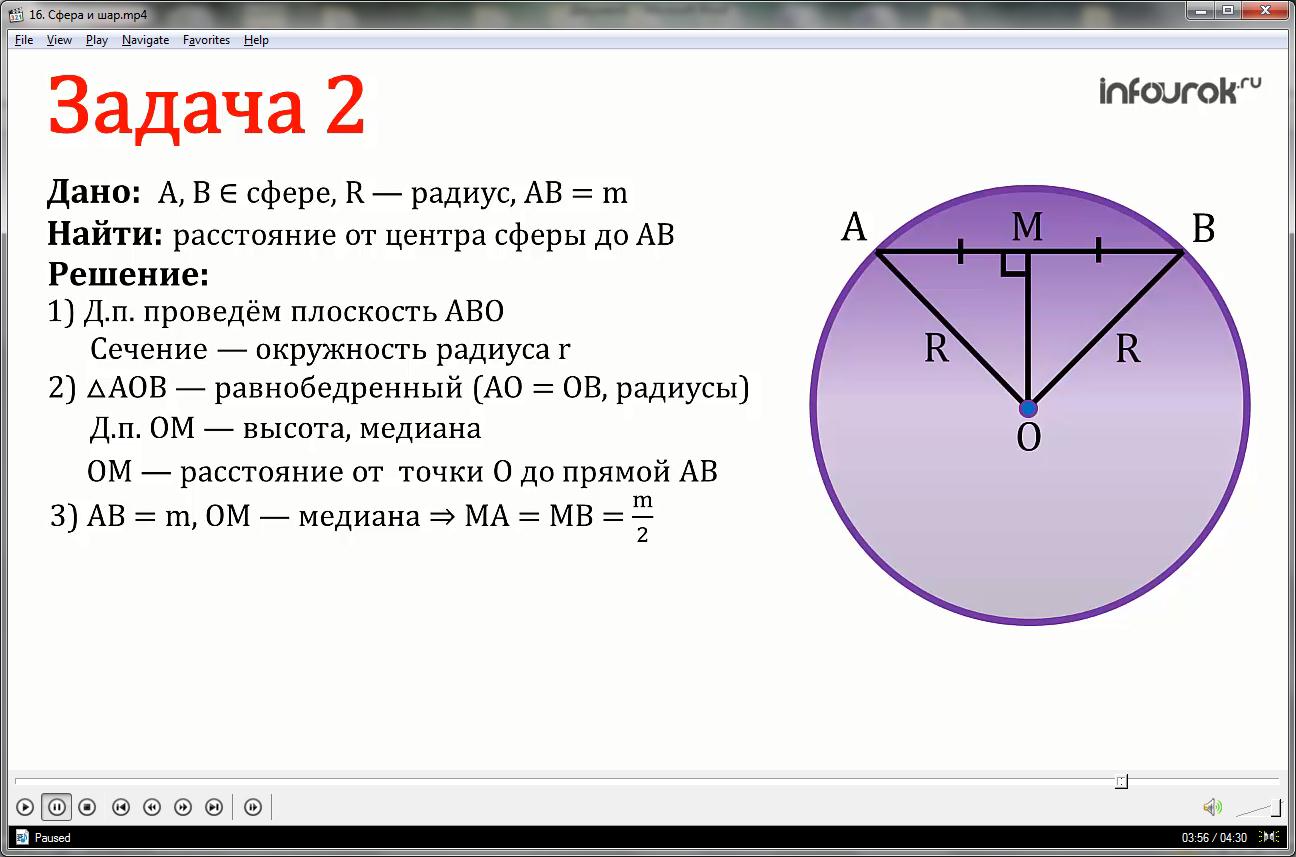
Точки А и В лежат на сфере радиусом R. Найти расстояние от центра сферы до прямой АВ, если АВ=m.
Решение:
1.Дополнительное построение: проведём плоскость через точки А, В и О (центр сферы).
В сечении получим окружность радиуса r.
2.Треугольник АОВ — равнобедренный, так как АО и ОВ — радиусы.
Дополнительное построение: проведём высоту ОМ, которая является и медианой.
ОМ — искомое расстояние от центра сферы до прямой АВ.
Найдём его.
3.Поскольку АВ=m, ОМ — медиана, то
МА=МВ=
4. Найдём ОМ из прямоугольного треугольника АОМ по теореме Пифагора:
ОМ= = =
Итак, расстояние от центра сферы до прямой АВ равно
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 10317 |
| Номер материала | 1002 |