
Урок "Способ подстановки"

Краткое описание документа:
Линейные уравнения, имеющие две переменные, представляют собой основу для многих тривиальных задач. Поэтому важно уметь всегда найти подходящий корень, удовлетворяющий решению для обоих уравнений в системе. В прошлом видеоуроке мы рассматривали графический метод определения общей пары х и у. Для этого можно использовать визуализированное представление уравнений в виде графиков. Логично, что каждое уравнение является зависимостью между множеством х и множеством у. А точка пересечения, удовлетворяющая обе пары множества, есть ничто иное, как координатное представление корня системы уравнений.
Тем не менее, графический способ хоть и является наиболее наглядным, не очень удобен во многих жизненных случаях. Во-первых, он требует построения графиков в Декартовой системе координат. Во-вторых, не для каждого уравнения можно быстро и надежно построить график. И в третьих, графики не обладают достаточной точностью для многих вычислений, что делает использование графического метода при решении некоторых систем уравнений просто невозможным.
Наиболее универсальным является метод подстановки – с ним мы и ознакомимся в этом видео. Для выяснения теоретической основы данного метода, рассмотрим такой пример. Найти корни уравнения вида:
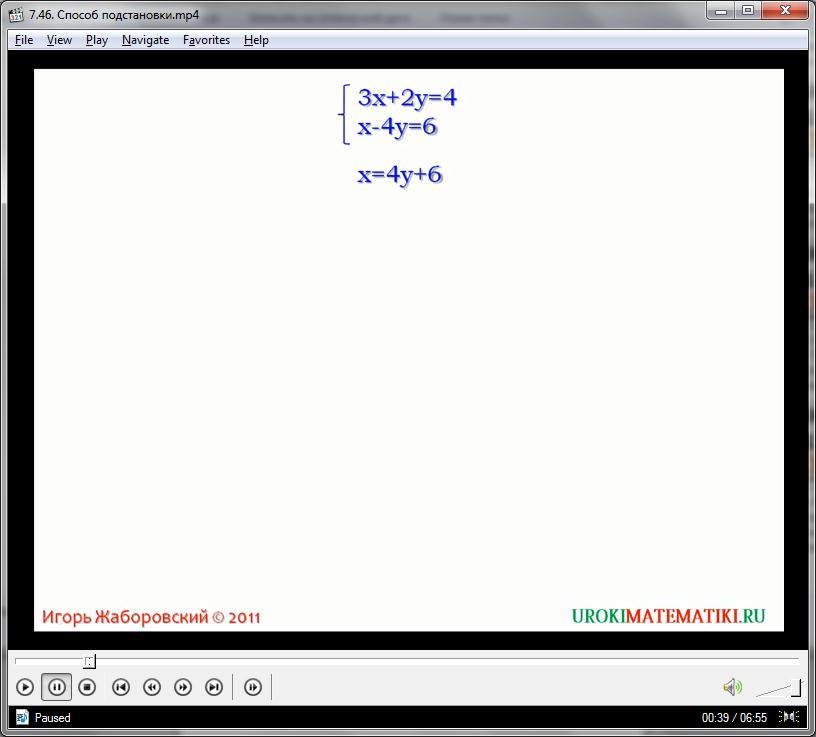
3х + 2у = 4
х – 4у = 6
Преобразуем тождественным способом второе уравнение так, чтобы получилось равенство, левая часть которого состоит исключительно из одной переменной х:
3х + 2у = 4
х = 6 + 4у
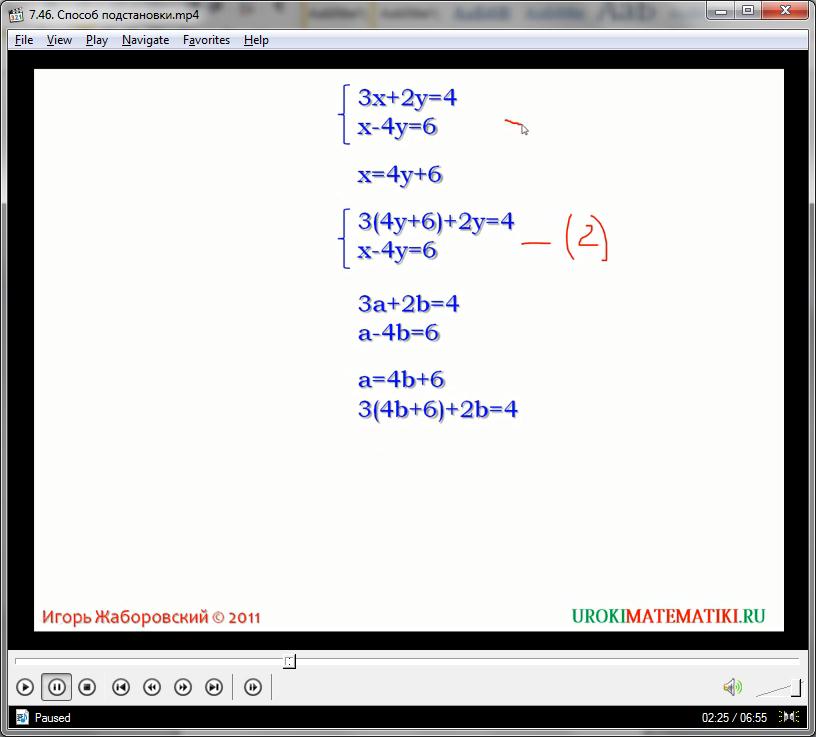
Как известно из самого определения системы уравнений, значения х и у являются строго одинаковыми для обоих равенств, следовательно, можно подставить полученное значение х (6 + 4у) в первое уравнение:
3(6 + 4у) + 2у = 4
х = 6 + 4у
Это преобразование дает нам обычное уравнение с одной неизвестной. Раскрываем скобки, приводим подобные слагаемые, перемещаем элементы так, что бы выразить у:
18 + 12у + 2у = 4
14у = 4 – 18
14у = - 14
у = -1
Таким образом, нам удалось найти значение переменной у. Аналогично мы можем подставить полученное число во второе уравнение, вместо самой у. Приводим выражение х:
х = 6 + 4у
х = 6 +4(-1)
х = 2
Мы определили корни для системы уравнений методом подстановки – в нашем случае это (2, -1).
Разработаем общий алгоритм действий для решения любой системы уравнений. Отметим сразу, что не все абсолютно системы решаются данным методом, но большинство. Итак, если нам задана система линейных уравнений с двумя переменными:
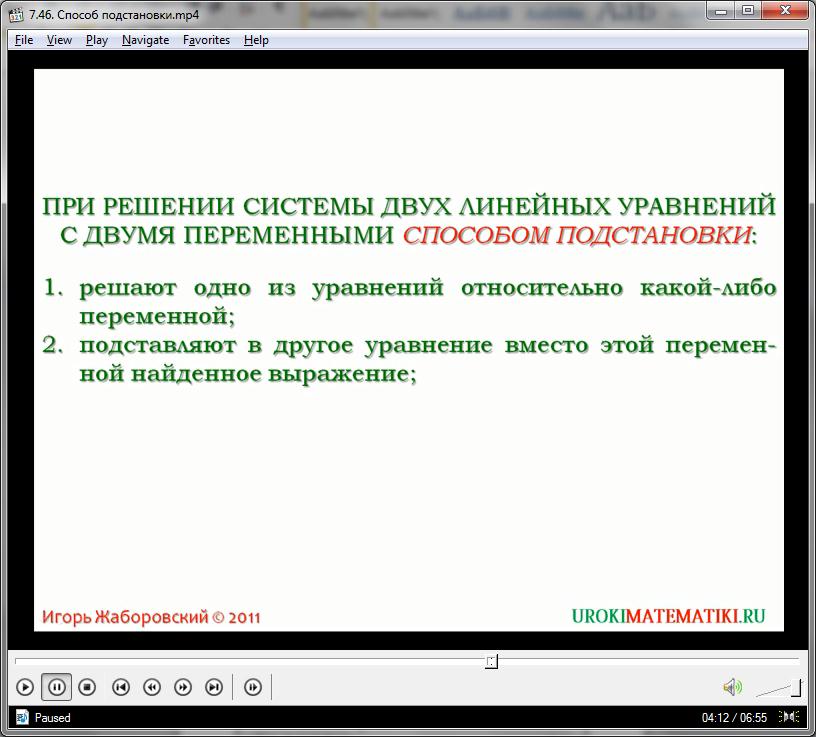
- Выражаем одну переменную, через уравнение, и вторую переменную. При этом пользуются любым удобным равенством, которое позволяет определить переменную без сложных действий;
- Подставляем полученное выражение переменной в другое уравнение (в то, которое не использовалось для выражения!);
- Решаем полученное уравнение с одной неизвестной, путем тождественных преобразований, и выражения переменной, как итог;
- Подставляем полученное значение переменной в первое выражение и рассчитываем вторую переменную;
- Важно использовать перекрестное решение системы – не рекомендуется выражать переменные и проводить вычисления над одним, и тем же уравнением.
Чаще всего, такое уравнение просто обнулится по обеим частям.
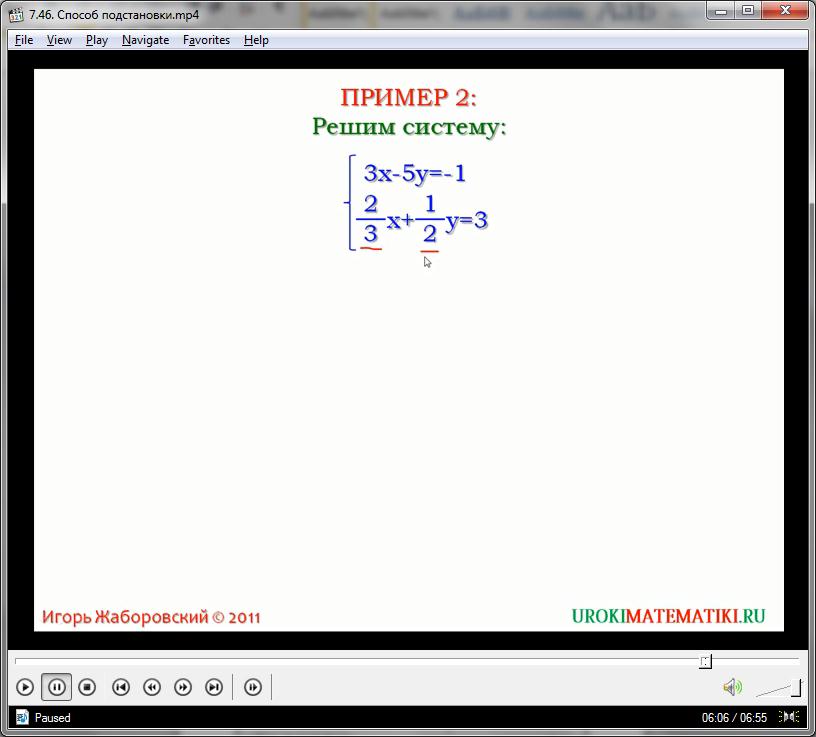
Для практики, решим такой пример. Найти корни уравнения:
5х – 2у = 16
10х – 3у = 27
Выражаем переменную у в первом уравнении:
5х – 2у = 16
-2у = 16 – 5х
у = (5х – 16)/2
Подставляем полученное значение переменной во второе уравнение:
10х – 3у = 27
у = (5х – 16)/2
10х – 3((5х – 16)/2) = 27
Чтобы решить это уравнение с одной неизвестной х, умножим обе части на два, раскроем скобки и приведем подобные слагаемые:
10х – 3((5х – 16)/2) = 27
20х – 3(5х – 16) = 54
20х – 15х + 48 = 54
5х = 6
х = 1,2
Подставляем полученное значение переменной в выражение для у:
у = (5х – 16)/2
х = 1,2
у = (6 – 16)/2
у = -5
Корнями заданной системы является пара (1,2, -5).
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4897 |
| Номер материала | 478 |