
Урок "Сравнение десятичных дробей"

Краткое описание документа:
Видеоурок «Сравнение десятичных дробей» - наглядное пособие, предназначенное для использования на уроке математики по данной теме. Урок построен таким образом, что может использоваться в качестве части урока, полностью заменяя объяснение учителя по новой теме. Также учитель может его применять как наглядное пособие, сопровождая демонстрацией свое объяснение. В ходе видеоурока описываются все важные детали, которые необходимо учесть при сравнении десятичных дробей. Тема раскрывается, поэтапно вводя новые правила, чтобы достичь глубокого понимания материала. Таким образом, цели урока достигаются быстрее.

В демонстрации использованы приемы, повышающие наглядность материала. С помощью различных шрифтов выделяется текст, который требует запоминания. Анимационные эффекты помогают последовательно и детально представить информацию. Голосовое сопровождение текста представляет собой объяснение учителя, дополняя видео важными комментариями и повышая эффективность воздействия на мыслительные процессы ученика.
Демонстрация видеоурока начинается с представления названия темы урока. Демонстрируются различные записи одинаковых десятичных дробей на примере преобразования длины отрезка. Для этого изображается отрезок АВ, длина которого 6 см. Отмечается, что длину отрезка также можно представить в мм, то есть она составляет 60 мм. Необходимо представить длину отрезка в дециметрах. Зная соотношения различных единиц измерения, можно вспомнить, что 1см – это 1/10 дм, а 1 мм – это 1/100 дм. Соответственно, длина 6 см=6/10 дм, а 60мм=60/100 дм. Представив эти величины с помощью десятичной записи, отмечается, что АВ=0,6 дм из первого соотношения и АВ=0,60 дм из второго соотношения.
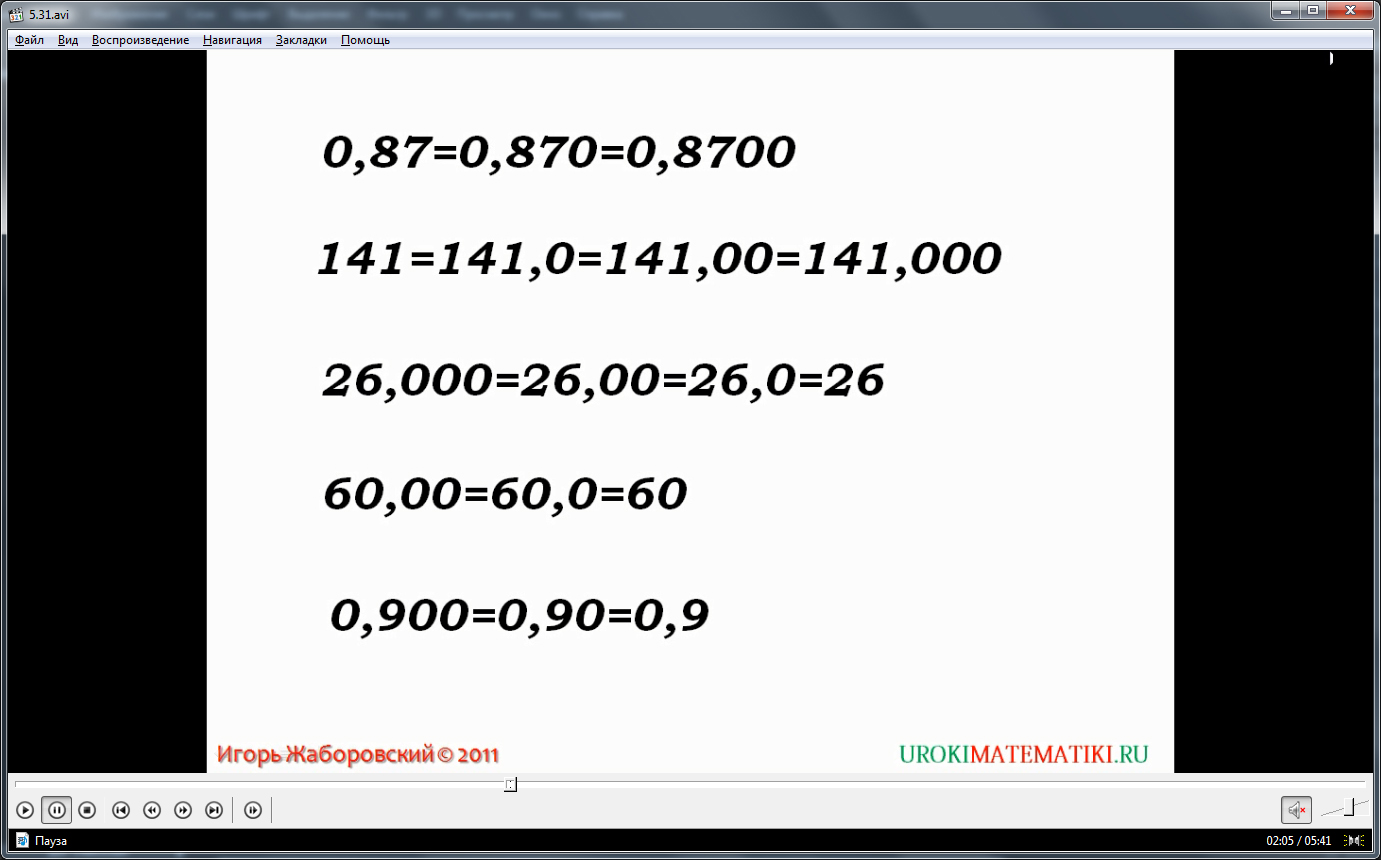
Так как полученные числа выражают одну и ту же величину отрезка АВ в дециметрах, между данными десятичными дробями можно поставить знак равенства, то есть 0,6дм=0,60дм. Этот пример свидетельствует о том, что при дописывании справа от дроби нуля, ее значение не изменяется. Ниже примера сформулировано правило, которое гласит, что при дописывании нулей к дробной части справа или отбрасывании нуля, значение десятичной дроби не меняется. Для усвоения материала приводятся примеры равных дробей 0,87=0,870=0,8700, 141=141,0=141,00=141,000, 26,000=26,00=26,0=26, 60,00=60,0=60 а также 0,900=0,90=0,9. Отмечается, что независимо от того сколько нулей дописано справа дробной части десятичной дроби, ее значение остается неизменным. Поэтому, если в задачах встречаются примеры, в которых справа от дробной части есть нули, их можно отбрасывать, оставляя только значимую часть.
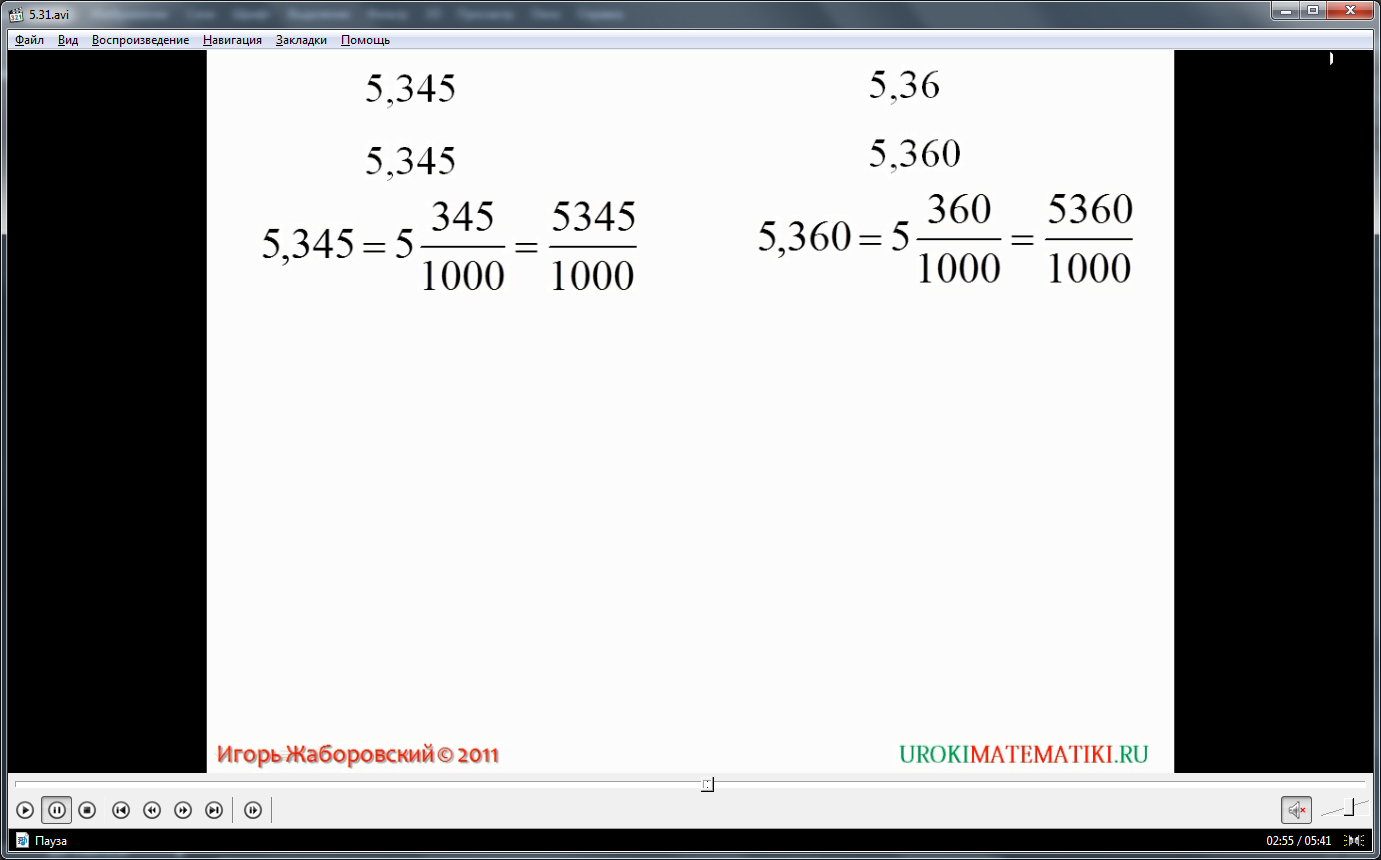
Далее рассматривается материал о сравнении десятичных дробей. Представляются два числа – 5,345 и число 5,36. Для сравнения этих дробей предлагается уравнять число знаков после запятой. Для этого справа от числа 5,36 приписывается нуль – получается 5,360. Затем числа представляются в виде неправильной дроби. Ученикам напоминается, как преобразуются в неправильную дробь смешанные числа: 5,345=5+345/1000=5345/1000 и 5,360=5+360/1000=5360/1000. Полученные неправильные дроби имеют одинаковые знаменатели, поэтому для их сравнения необходимо сравнить числители, то есть большей будет та дробь, числитель которой больше. Сравниваются числители 5345<5360. Отмечается, что на основании этого можно утверждать, что 5345/1000<5360/1000. А это значит, что число 5,345 меньше 5,360. На экране выделено выражение сравнения двух десятичных дробей. Ниже представлено правило сравнения двух десятичных чисел. В нем указано, что для этого необходимо сначала уравнять количество знаков после запятой, дописав необходимое количество нулей, а затем отбросить запятую и сравнить натуральные числа.
Описывается правило, как отмечается на координатном луче десятичная дробь. В правиле указывается, что десятичные числа изображаются на координатной прямой так же, как и обыкновенные дроби. Для примере берется дробь 0,4. Чтобы отметить положение данного числа на координатной прямой, оно сначала представляется обыкновенной дробью 0,4=4/10. На экране изображается координатный луч, на котором отмечена единица, а интервал между 0 и 1 разбит на 10 равных частей. Соответственно, дробь 4/10 означает точку, которая отсчитывает от начала отсчета 4 части из 10 – на прямой она отмечается как точка А. На этой же прямой отмечается точка 0,6, указывая при этом, что равные точки 0,6=0,60, которые рассматривались ранее, отмечаются на координатном луче одинаковыми точками. Также ниже формулируется правило, в котором определяется взаимное расположение точек разной величины. Оно характеризуется тем, что точки, которые соответствуют большему числу, отмечаются правее точек с меньшей координатой, а точки с меньшей координатой располагаются левее большей. На изображенной прямой примером служит расположение точек 0,4 и 0,6. Так как точка 0,6 больше 0,4, то она располагается правее точки 0,4. Также отмечается точка 0,8, которая располагается правее точки 0,6. Точки на координатном луче располагаются в соответствии с выражением 0.4<0.6<0.8.
Занятие заканчивается контрольными вопросами, на которые нужно ответить ученикам, чтобы проверить , как хорошо они усвоили учебный материал. Им необходимо объяснить соотношение десятичных дробей, к которым справа приписываются один или несколько нулей, а также повторить правило сравнения десятичных чисел.

Видеоурок «Сравнение десятичных дробей» рекомендуется применять на уроке математики в школе для повышения эффективности обучения, улучшения наглядности представления учебной информации. Также данное наглядное пособие будет полезно учителю, который подает тему дистанционно. Если ученику требуется дополнительный материал для усвоения темы или он изучает ее самостоятельно, видеоурок станет лучшим помощником, помогающим усвоить материал.
| Автор | |
|---|---|
| Дата добавления | 28.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 6059 |
| Номер материала | 391 |