
Урок "Сложение и вычитание смешанных чисел"

Краткое описание документа:
Видеоурок «Сложение и вычитание смешанных чисел» - наглядный материал для освоения пятиклассниками умение решать примеры, в которых требуются знания о сложении и вычитании смешанных чисел. В течение демонстрации видео ученики знакомятся с правилами выполнения вычислений, усваивают материал, наблюдая за описанием примеров, в которых требуется применять данные знания. Видео может использоваться в качестве самостоятельной части урока для объяснения новой темы, а также сопровождать объяснение учителя, обеспечивая его наглядность.
Благодаря использованию иллюстраций и анимационных эффектов, видеоурок понятно объясняет тему урока, обеспечивая ее глубокое понимание. Используя различные способы выделения текста, обеспечивается лучшее запоминание важных правил, выделяются особенности порядка вычислений, помогая запомнить и освоить материал. Озвучивание видео дает возможность дополнить его важными комментариями, полностью заменить учителя в части урока, где требуется объяснение нового материала.
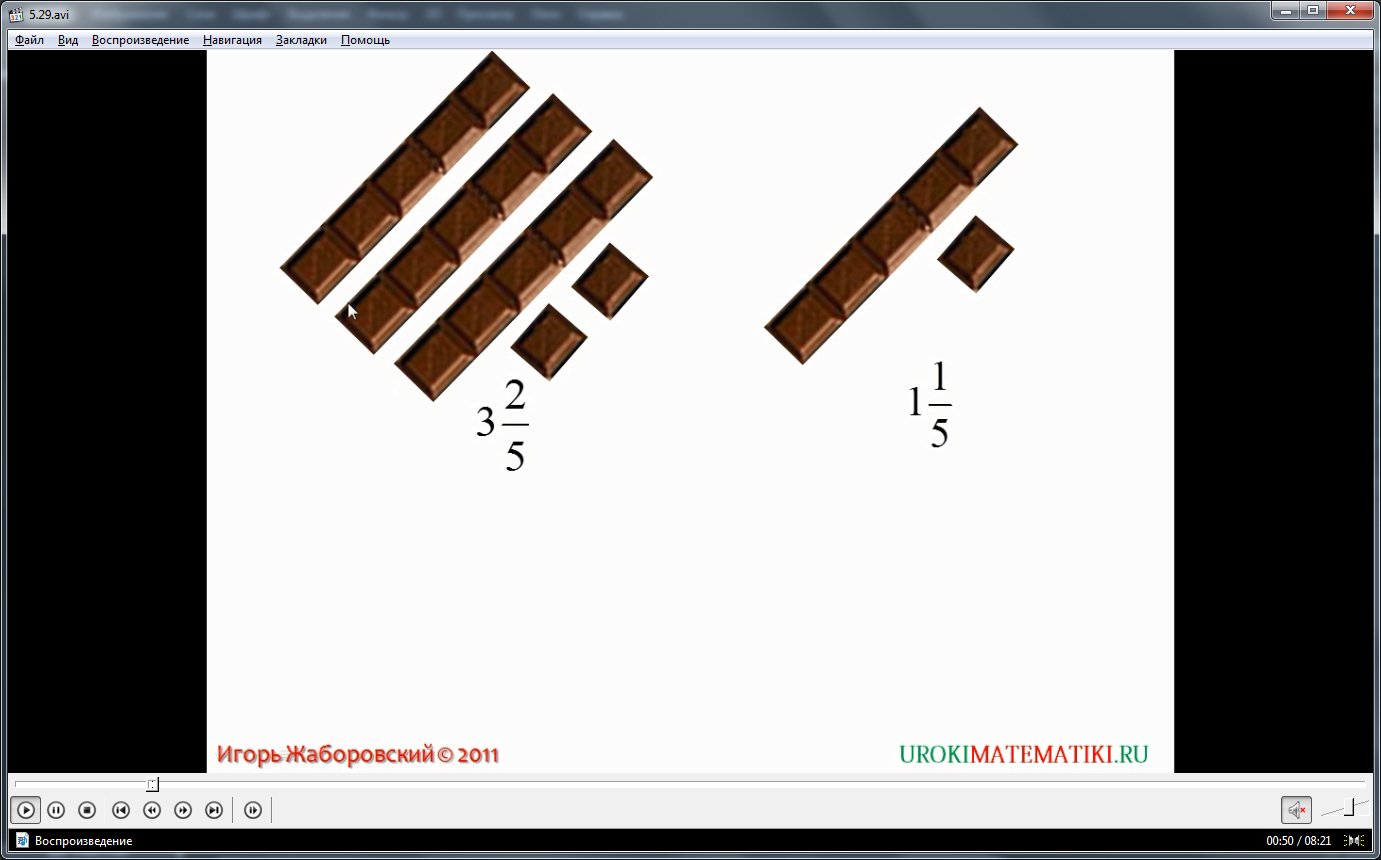
Видеоурок начинается с представления темы урока. Затем на иллюстрированном примере раскрывается порядок выполнения действий сложения и вычитания со смешанными числами. Отмечается, что правила оперирования смешанными числами основаны на свойствах сложения и вычитания. На экране представляется три плитки шоколада, каждая их которых состоит из 5 частей и еще 2 кусочка, то есть, основываясь на знаниях о смешанных числах, можно утверждать, что на столе лежит 3+2/5 плитки шоколада. На стол докладывается еще 1 плитка шоколада и 1 кусочек, то есть 1+1/5 шоколадки. Задается вопрос, сколько шоколада лежит на столе с учетом доложенного, то есть фактически необходимо сложить (3+2/5)+(1+1/5). Зная. Что каждое смешанное число представляет сумму целой и дробной части, представляем данную сумму в виде 3+2/5+1+1/5. Зная, что поменяв местами слагаемые, мы получим одинаковый результат, слагаемые перераспределяются так, чтобы получить отдельно сумму целых частей и сумму дробных частей. Задание сводится к сложению натуральных чисел и сложению дробей с одинаковыми знаменателями. В результате их сложения получаем 3+1+2/5+1/5=4+3/5. Таким образом, задача решена – мы получили смешанное число, которое демонстрирует, что на столе оказались 4 целых плитки шоколада и еще 3 кусочка (3/5). Справедливость решения можно отследить по рисунку – на столе оказались 4 целые плитки и три кусочка. На рисунке демонстрируется краткая запись решения (3+2/5)+(1+1/5)=4+3/5.
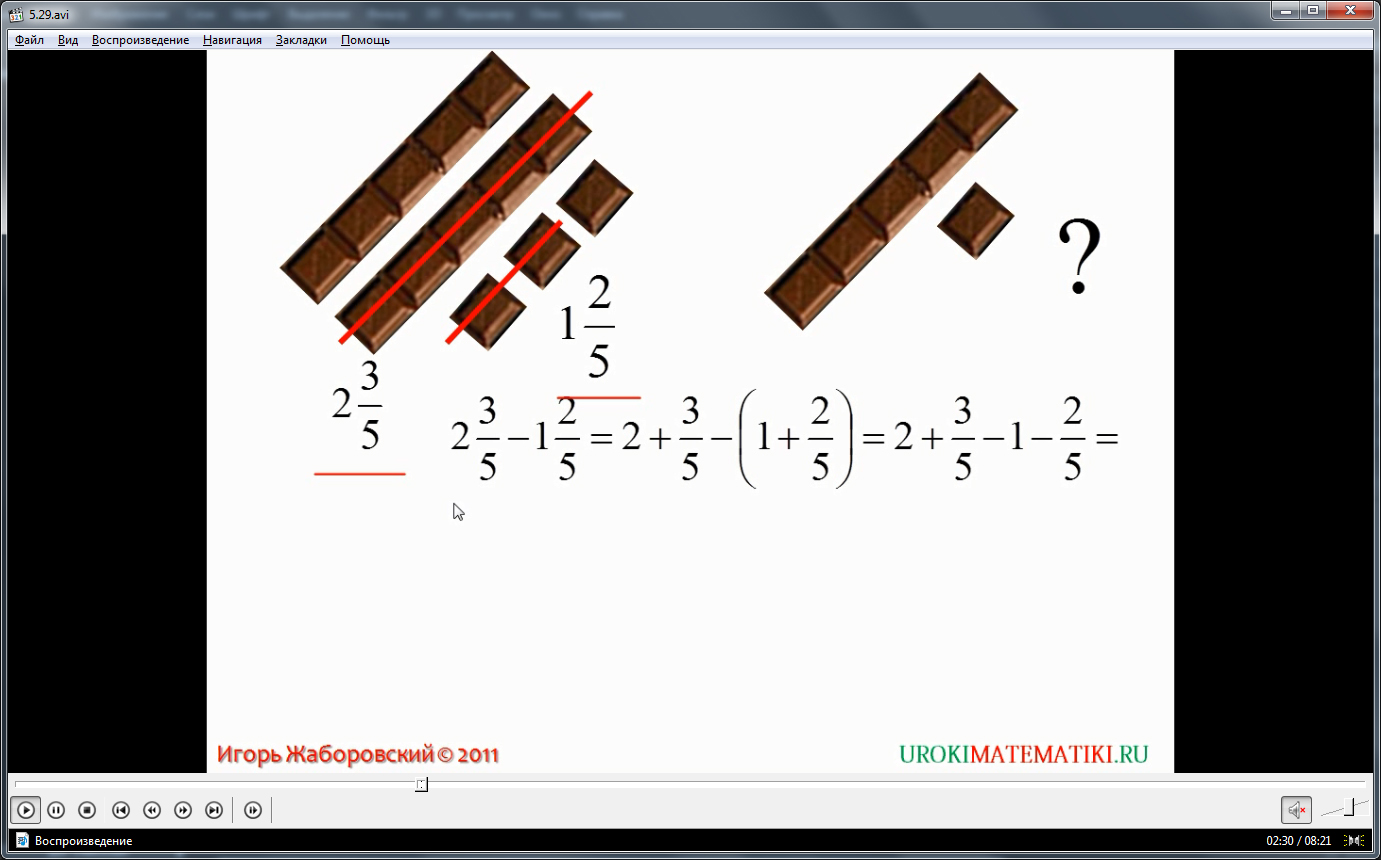
В описании решения второй задачи демонстрируется, как выполняется вычитание смешанных чисел. На рисунке показано, что на тарелке лежит 2 плитки шоколада и еще 3 кусочка, то есть 2+3/5. Указано, что съели одну целую плитку шоколада и два кусочка, то есть 1+2/5. Необходимо определить, сколько шоколада осталось на тарелке. Фактически необходимо вычесть из 2+3/5 число 1+2/5. Вспомнив, что каждое из этих чисел представляет сумму целой и дробной части, представляем разность в виде (2+3/5)-(1+2/5). Чтобы выполнить действия над числами, следует воспользоваться свойствами сложения и вычитания. Сначала открываются скобки, в которые заключено второе смешанное число 2+3/5-1-2/5. Затем перераспределяем числа так, чтобы отдельно найти разность целых чисел и отдельно – дробных чисел (2-1)+(3/5-2/5). Вычислив значения в скобках, находим искомое число 1+1/5. Следовательно, на тарелке остались 1 плитка шоколада и 1 кусочек. Также представляется краткая запись решения задания (2+3/5)-(1+2/5)=1+1/5. Проверить справедливость решения также можно по рисунку – на нем хорошо видно, что на тарелке осталась 1 плитка и 1 кусочек шоколада.
Далее представляется общее правило выполнения действий над смешанными числами. На экран выводится правило, что для выполнения действий со смешанными числами (сложения и вычитания), отдельно производятся действия над целыми и дробными частями. Также делается замечание, что если в действиях участвует неправильная дробь, ее сначала представляют в виде смешанного числа – выделяют целую часть, которую затем добавляют к имеющейся целой части числа. Ниже правил представлен пример сложения смешанных чисел 3+7/9+2+4/9. При сложении данных чисел получается 5+11/9. Чтобы привести данную дробь к нормальному виду, из ее дробной части выделяют целую часть: 119=1+2/9, поэтому в результате получаем сумму 5+1+2/9. Сложив числа, получаем результат произведенных действий 6+2/9.

Делается еще одно важное замечание для операции вычитания, которое указывает, как поступать в случае, когда дробная часть вычитаемого больше дробной части уменьшаемого. Отмечается, что определив эту особенность в условии задания, необходимо воспользоваться возможностью увеличить числитель дробной части уменьшаемого за счет целой части. Для этого числа представляются в виде суммы (6+3/7)-(2+5/7), а затем из целой части уменьшаемого выделяется 1, то есть (5+1+3/7)-(2+5/7). Смешанное число 1+3/7 представляем в виде неправильной дроби 10/7. После выполненных преобразований получаем разность, которую легко решить, пользуясь известными правилами 5+10/7-(2+5/7)=3+5/7. Также предлагается освоить краткую запись выполненного задания (6+3/7)-(2+5/7)= 5+10/7-(2+5/7)=3+5/7. Диктор подробно повторяет, как выполнялись действия, на что обращалось внимание, сопровождая объяснение анимационными эффектами, чтобы акцентировать внимание учеников на важных деталях.
Также представляется порядок действий для нахождения разности натурального числа и дроби. На экране формулируется правило, согласно которому, для выполнения вычислений сначала из уменьшаемого выделяют дробную часть, представив в виде дроби единицу, то есть 4-5/8=(3+8/8)-5/8. Так как над такими числами ученики уже умеют выполнять действия, находится значение разности 4-5/8=3+3/8. Правило выделено цветным шрифтом, подчеркивая его важность. Для усвоения материала демонстрируется еще один пример 8-(3+5/6). Из числа 8 извлекается 1, которая превращается в дробь 6/6. Таким образом, получаем разность смешанных чисел, решение которой уже освоено (7+6/6)-(3+5/6)=4+1/6.

В качестве итога занятия предлагается ответить на вопрос о том, как складываются и вычитаются смешанные числа.
Видеоурок «Сложение и вычитание смешанных чисел» рекомендуется использовать для повышения эффективности урока математики. Также материал будет полезен учителю, который преподает тему ученикам дистанционно. Материал может быть предложен ученикам для самостоятельной проработки, если они недостаточно хорошо усвоили его на уроке или осваивают тему на дому.
| Автор | |
|---|---|
| Дата добавления | 28.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 6202 |
| Номер материала | 1104 |