
Урок "Одночлен. Умножение одночленов"

Краткое описание документа:
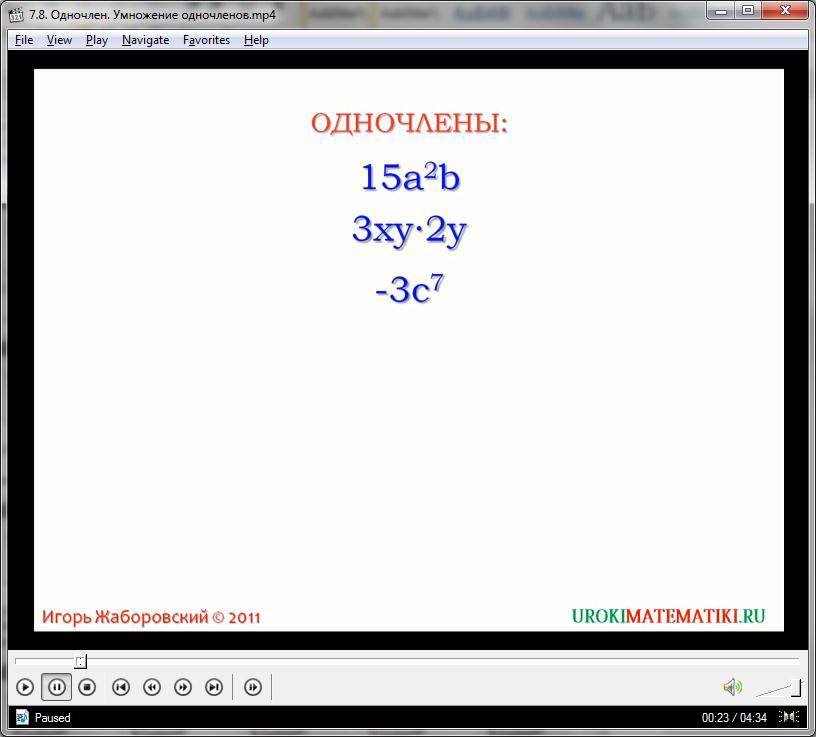
Одночлен – это одна из базовых математических конструкций линейной алгебры. В прошлых видеоуроках мы уже сталкивались с такими выражениями, как -7, ах, (3ас)2 – они все являются одночленами, или же, мономами. Одночлен – это достаточно универсальное выражение, имеющее некоторое значение, и представленное тремя основными показателями: числовым коэффициентом, буквенной переменной, значением степени выражения. Наиболее базовым является числовой показатель – он есть всегда, в любом мономе. Без числа весь смысл одночлена теряется, и его значение перестает быть действительным. Если же в примерах встречается выражения типа х, -(у)2, то следует понимать, что в данном случае мы имеем дело с невидимым числовым коэффициентом, равным единице. Любое свободное число, например 5, 13, так же являются одночленами.
Переменная является непостоянным элементом. Иногда она задается одной либо же несколькими перемноженными неизвестными (причем в одночлене знак умножения опускается), но может также вовсе отсутствовать.
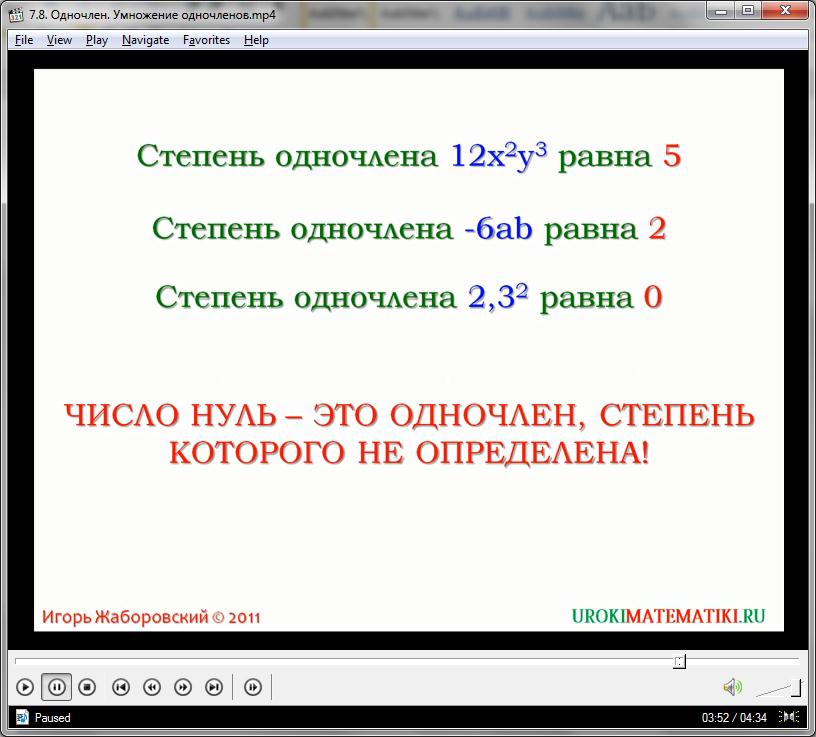
Важным показателем любого одночлена является степень. Стоит отличать степень одночлена от степени элементов, которые входят в него! Степень одночлена, в общем смысле, представляет собой сумму степеней переменных, например, степень одночлена 7а3х5 равна 3+5 = 8.
Степень свободного числа 7 (к примеру) всегда равна единице. А вот степень 7, как одночлена, равна нулю, так как для одночлена задается сумма степеней именно буквенной переменной, которая в мономе «7» отсутствует. Число 0 может быть одночленом, но только с неопределенной степенью. У всех действительных мономов степень может принимать только натуральные и положительные значения. Следует помнить, что если степень явно не указана, то она равна единице.
Одночлен, как и свободное значение, имеет такую характеристику, как положительность/отрицательность. Знак этого параметра, как правило, задается перед всем выражением и относится сугубо к числовому коэффициенту (множителю). В противном случае, если какая-либо переменная задана отрицательной, то её помещают вместе с минусом в отдельное скобки, например:
Отрицательный одночлен с числовым коэффициентом, равным -1: -а2ху
Положительный одночлен с отрицательной переменной х: а2(-х)у
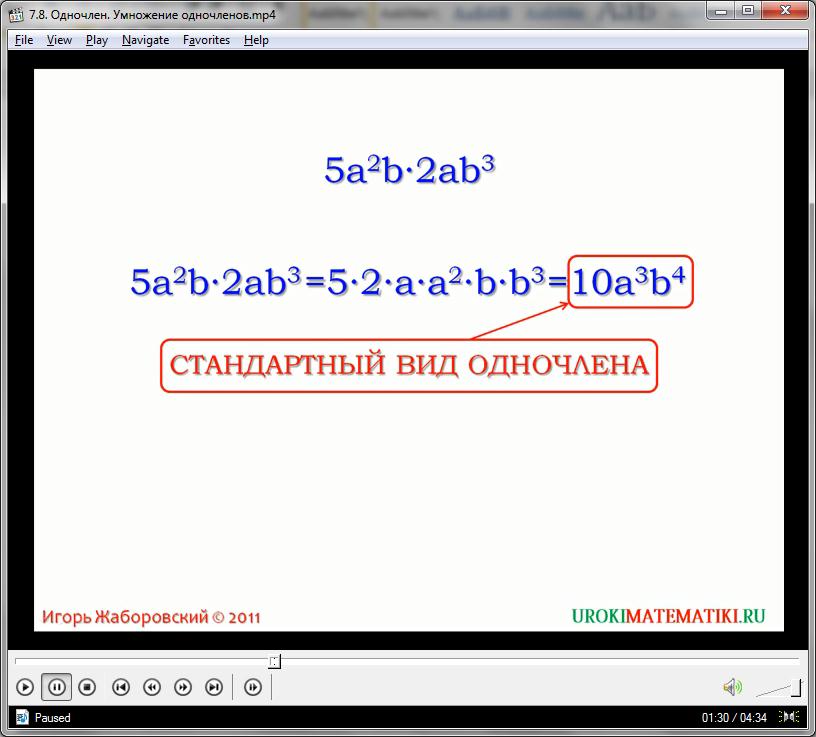
Как правило, одночлены принято сокращать и записывать в удобном, стандартизированном виде. Часто такая процедура и представляет собой задания в этой теме. Например, упростим выражение вида:
5(а)2х2а(х)3
Воспользуемся свойствами степеней, рассмотренными в предыдущем видеоуроке, и общими правилами умножения:
5(а)2х2а(х)3 = 5*2*(а)2а*(х)3х = 10(а)3(х)4
Перегруппировав множители для удобства и совершив произведения подобных выражений, мы получили итоговый одночлен. Подобную форму выражения принято называть стандартной. В этом случае числовой коэффициент, образованный перемножением всех свободных чисел в одночлене, выносится наперед. Далее идут переменные, предварительно сгруппированные по основанию и перемноженные для сокращения. Степени записываются в обычном порядке, в верхнем правом индексе.
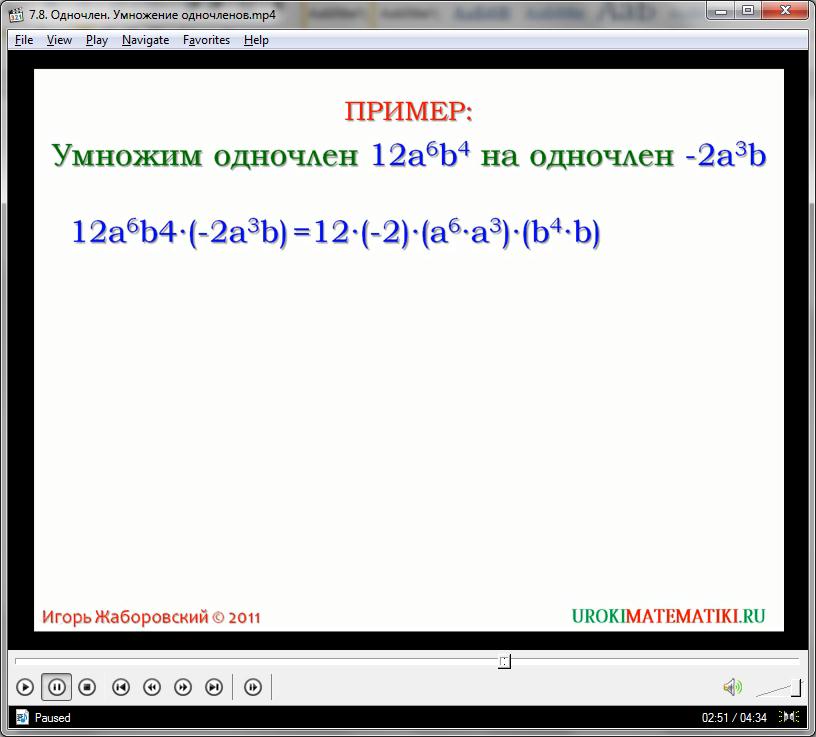
Решим упражнение. Найдем произведение одночленов:
12а6х4 * -2а3х
Воспользуемся правилами перегруппировки, рассчитаем:
12а6х4 * -2а3х = 12*(-2)*а(6+3)*х(4 + 1) = -24а9х5
Старые математические руководства дают более широкое определение понятию «Одночлен». Согласно им это такое выражение, последним действием которого является умножение или деление. На сегодняшний день такое определение устарело, но оно прекрасно иллюстрирует тот факт, что произведение вида nху * nас является не только умножением двух независимых одночленов nху и nас, но и общим мономом 2nхуnас.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5354 |
| Номер материала | 482 |