
Урок "Об аксиомах в геометрии"

Краткое описание документа:
Видеоурок «Об аксиомах геометрии» рассматривает одну из наиболее важных тем, которая входит в фундамент данной науки. Задача данного видеоурока – ознакомить учеников с основными аксиомами евклидовой геометрии, дать представление о разнице между аксиомами и теоремами, провести некоторые обобщения изученного материала для формирования понятия о евклидовой геометрии.
Основное преимущество видеоурока – наглядность. Знание аксиом геометрии важно для формирования навыков доказательства утверждений, решения практических задач. Поэтому в нем используются инструменты, делающие материал легко запоминающимся. Данный видеоурок может стать самостоятельный блоком в ходе урока по данной теме, так как понятно и наглядно дает представление об аксиомах. Также видео может быть использовано в ходе объяснения учителя, сопровождая его рассказ наглядным материалом, выделяющим важные выводы и понятия.

Видеоурок начинается с объявления названия темы. Вначале ученикам напоминается, что на предыдущих уроках были доказаны ряд утверждений, которые требовали подтверждения из справедливости. При этом в ходе рассуждений были использованы уже доказанные ранее утверждения. Все данные утверждения называются теоремами. Однако первые теоремы опирались на утверждения настолько очевидные, что не требовали доказательств. Данные утверждения называются аксиомами. Эти утверждения составляют основу геометрии, так как на них строится вся наука. На экране продемонстрировано определение аксиомы как положения, которое является исходным и может быть использовано для доказательства теорем.
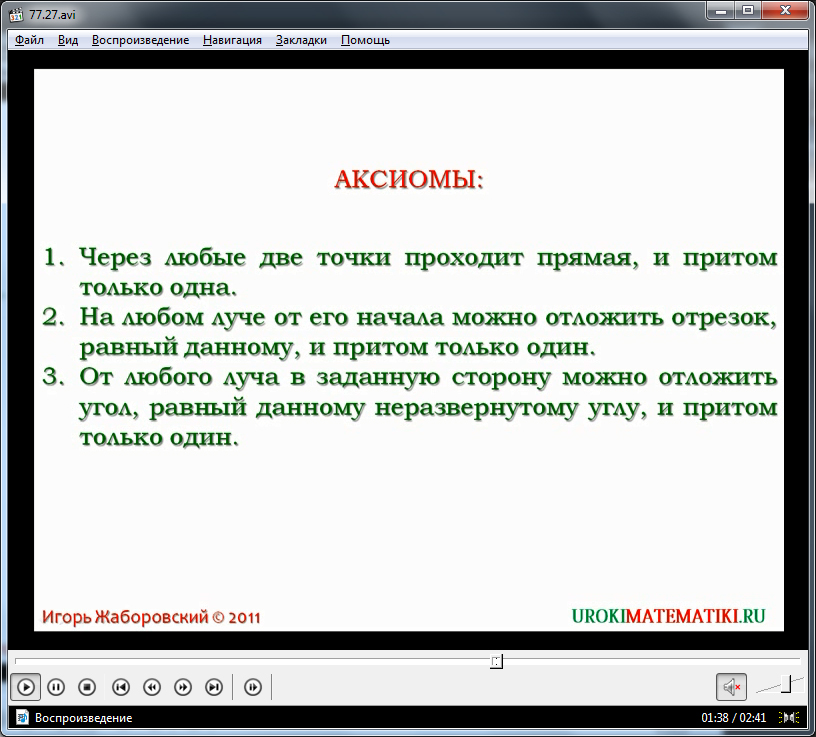
Несмотря на то, что понятие аксиомы вводится только на этом уроке, ученики уже не раз использовали аксиомы для доказательства утверждений. Отдельно на экране демонстрируется ряд аксиом, которые могут быть предложены учителем для записи в тетради и выделены для запоминания. Отмечается, что в доказательстве теорем была использована аксиома о том, что через две точки проводится только одна прямая. Остальные аксиомы фактически использовались, хотя и не были озвучены на предыдущих уроках.
Перед озвучиванием второй аксиомы ученикам напоминается, что при сравнении отрезков применялся способ наложения, корректность использования которого вытекает из еще одной аксиомы. Она утверждает, что на луче из его начала может быть проведен только один отрезок, равный данному.
Также отмечается, что третья аксиома геометрии была использована при выполнении сравнения двух углов. Она утверждает, что от имеющегося луча в определенную сторону может быть отложен только один неразвернутый угол, равный данному.
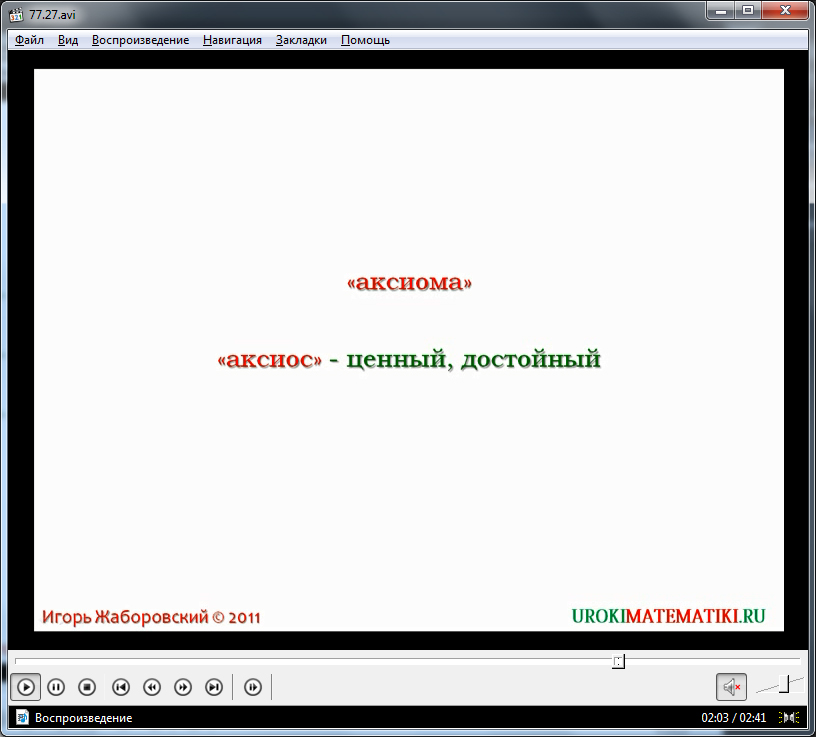
Представленные утверждения не требуют какого-либо доказательства, так как являются очевидными. Данные утверждения стали в основу науки еще в глубокой древности. Основы геометрии были изложены в Древней Греции, и происхождение слова «аксиома» - от греческого «аксиос», которое означает «ценный, или достойный». Информация о происхождении слова выведена на экран для лучшего запоминания. Ученики знакомятся с историей науки, метод доказательств которой отталкивается, прежде всего, от аксиом, а затем на использовании уже доказанных теорем. Они узнают, что данные аксиомы легли в основу труда «Начала», изложенного ученым Евклидом еще в Древней Греции. Постулаты Евклида и сегодня используются в геометрии. А сама наука по имени ученого называется евклидовой геометрией. В конце видео, следуя правилам преемственности обучения, анонсируется следующая тема из серии видеоуроков – рассмотрение первой аксиомы - одной из наиболее важных аксиом геометрии.
Видеоурок «Об аксиомах геометрии» может быть использован учителем на обычном уроке геометрии в школе для ознакомления с аксиомами, а также лечь в основу подобного урока при дистанционном обучении. Также данная информация будет полезна при самостоятельном ознакомлении с учебным материалом.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4537 |
| Номер материала | 514 |