
Урок «Усеченный конус»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Сегодня мы познакомимся еще с одной геометрической фигурой — усеченным конусом.
Возьмем произвольный конус и проведем секущую плоскость перпендикулярную его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей представляет собой конус, а другая называется усеченным конусом.
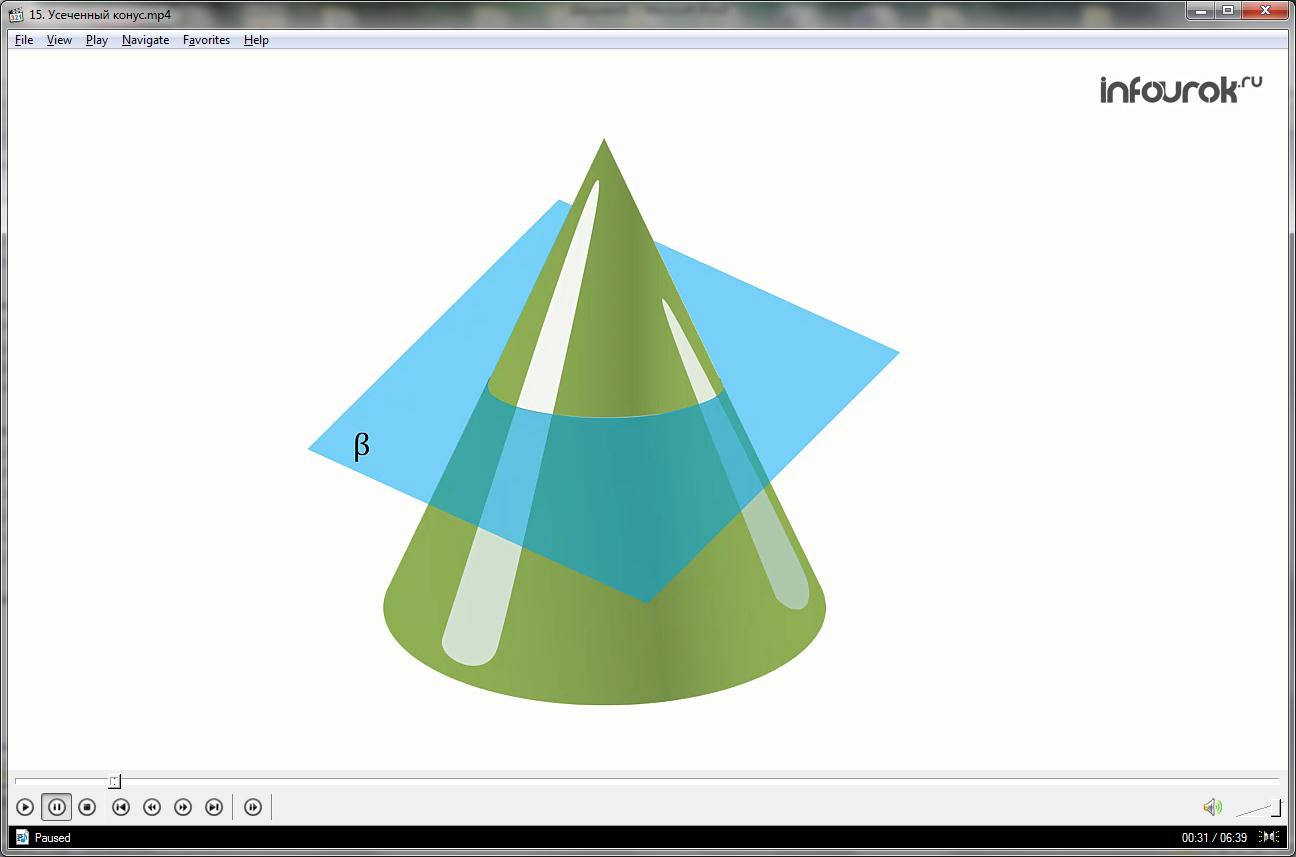
Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усеченного конуса, а отрезок, соединяющий их центры,— высотой усеченного конуса (ОО1).
Часть конической поверхности, ограничивающая усеченный конус, называется его боковой поверхностью (ABCD).
Отрезки образующих конической поверхности, заключенные между основаниями, называются образующими усеченного конуса (АВ).
Все образующие усеченного конуса равны друг другу.
Усеченный конус можно рассматривать как тело, полученное при вращении прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.
На рисунке показано вращение прямоугольной трапеции АА1О1О.
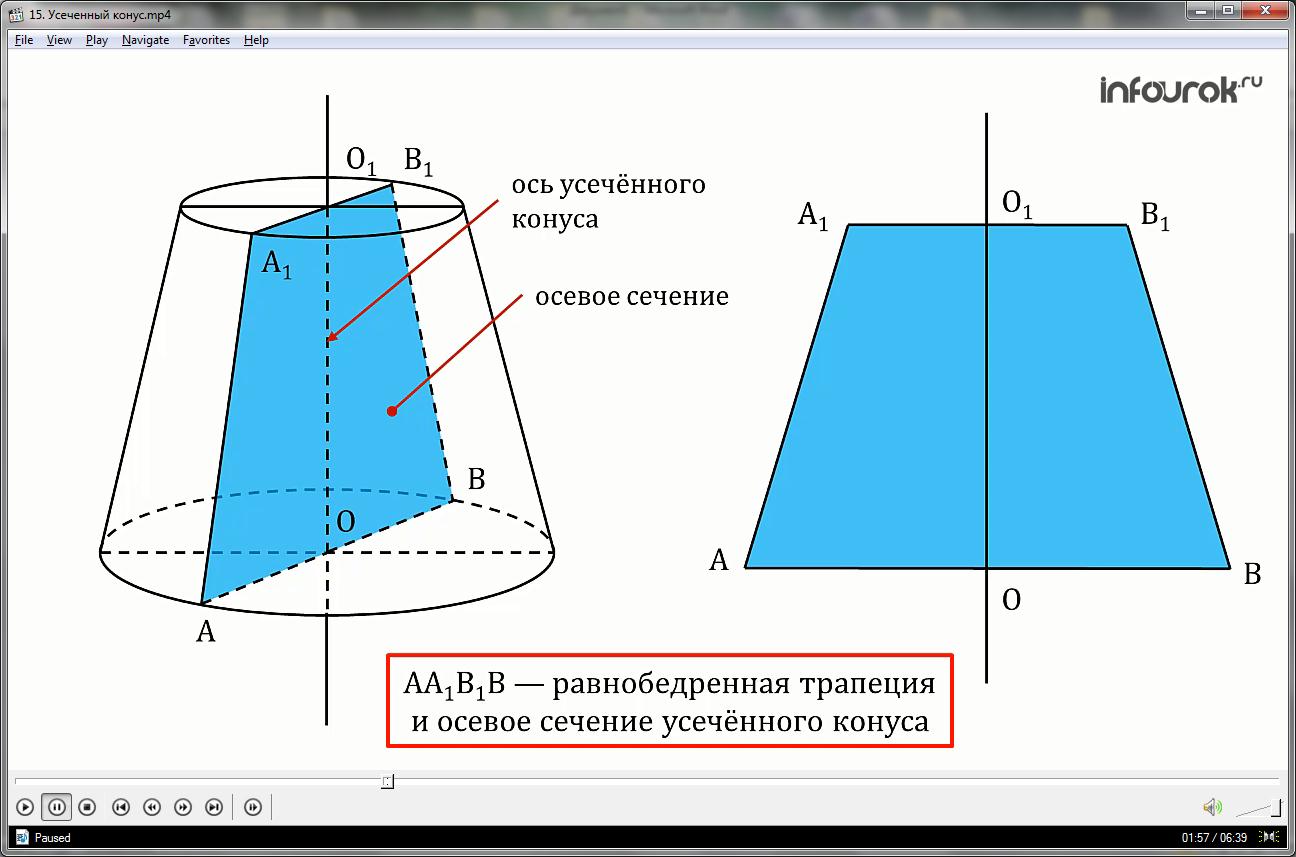
Прямая ОО1, соединяющая центры оснований, называется осью усеченного конуса. Сечение, проходящее через ось, называется осевым.
Осевое сечение является равнобедренной трапецией.
АА1В1В — равнобедренная трапеция и осевое сечение усеченного конуса.
Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.
Докажем это:

Пусть Р — вершина конуса, из которого получен усеченный конус, АА1 — одна из образующих усеченного конуса, радиус большего основания конуса больше радиуса меньшего основания,
точки О и О 1 — центры оснований.
Используя формулу площади боковой поверхности конуса: площадь боковой поверхности конуса равна произведению числа пи, радиуса основания и его образующей, получаем формулу: площадь боковой поверхности равна разности произведений числа пи на радиусы оснований и на образующую PA.
Заменим образующую РА на сумму
PA 1 + AA1 и получим такую формулу:
Отсюда, учитывая, что AA1 – образующая усеченного конуса, находим, что площадь боковой поверхности равна …
Выразим PA 1 через образующую конуса и радиусы большего и меньшего оснований.
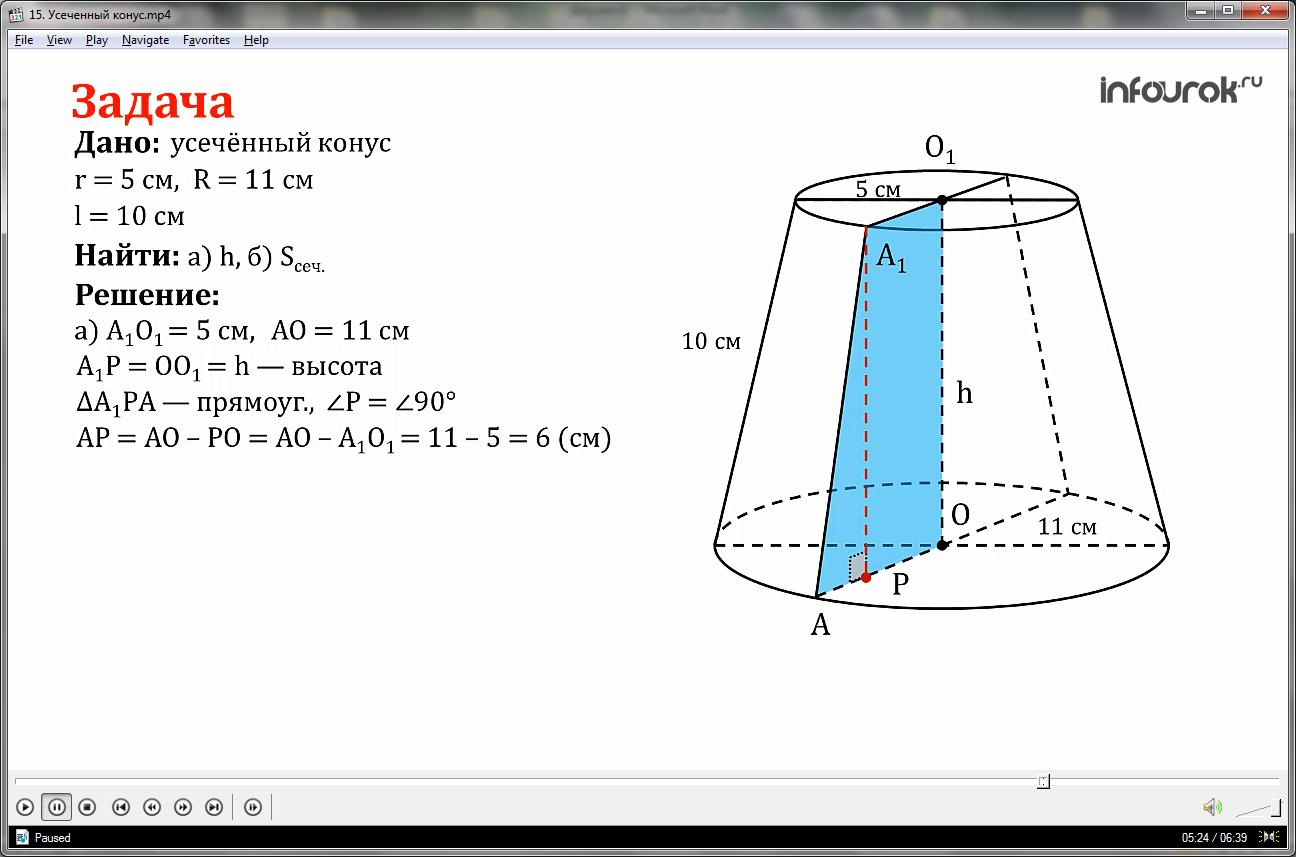
Прямоугольные треугольники РО1А1 и РОА подобны, так как имеют общий острый угол Р, поэтому получим равенство двух отношений: образующая меньшего конуса так относится к образующей большего конуса как радиус меньшего основания относится к радиусу большего основания.
Отсюда получаем, что образующую меньшего конуса можно представить как отношение произведения образующей усеченного конуса на радиус меньшего основания на разность радиусов оснований.
Подставив это выражение в формулу площади боковой поверхности,
получаем формулу: площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.
Площадь боковой поверхности усеченного конуса можно рассматривать как разность между площадями боковых поверхностей двух конусов. Поэтому развертка усеченного конуса – это часть круглого кольца.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 10680 |
| Номер материала | 1001 |