
Урок "Вписанная окружность"

Краткое описание документа:
В новом видео уроке мы рассмотрим такой геометрический объект, как вписанная окружность. По сути говоря, это, как стандарт, пара объектов, а именно некая окружность и многоугольник. При этом существуют строгие зависимости между некоторыми характеристиками вышеуказанных фигур, поэтому есть целая область геометрии, посвященная вписанным окружностям. Тщательное изучение свойств этой окружности позволит с легкостью решить любую задачу по этой теме.

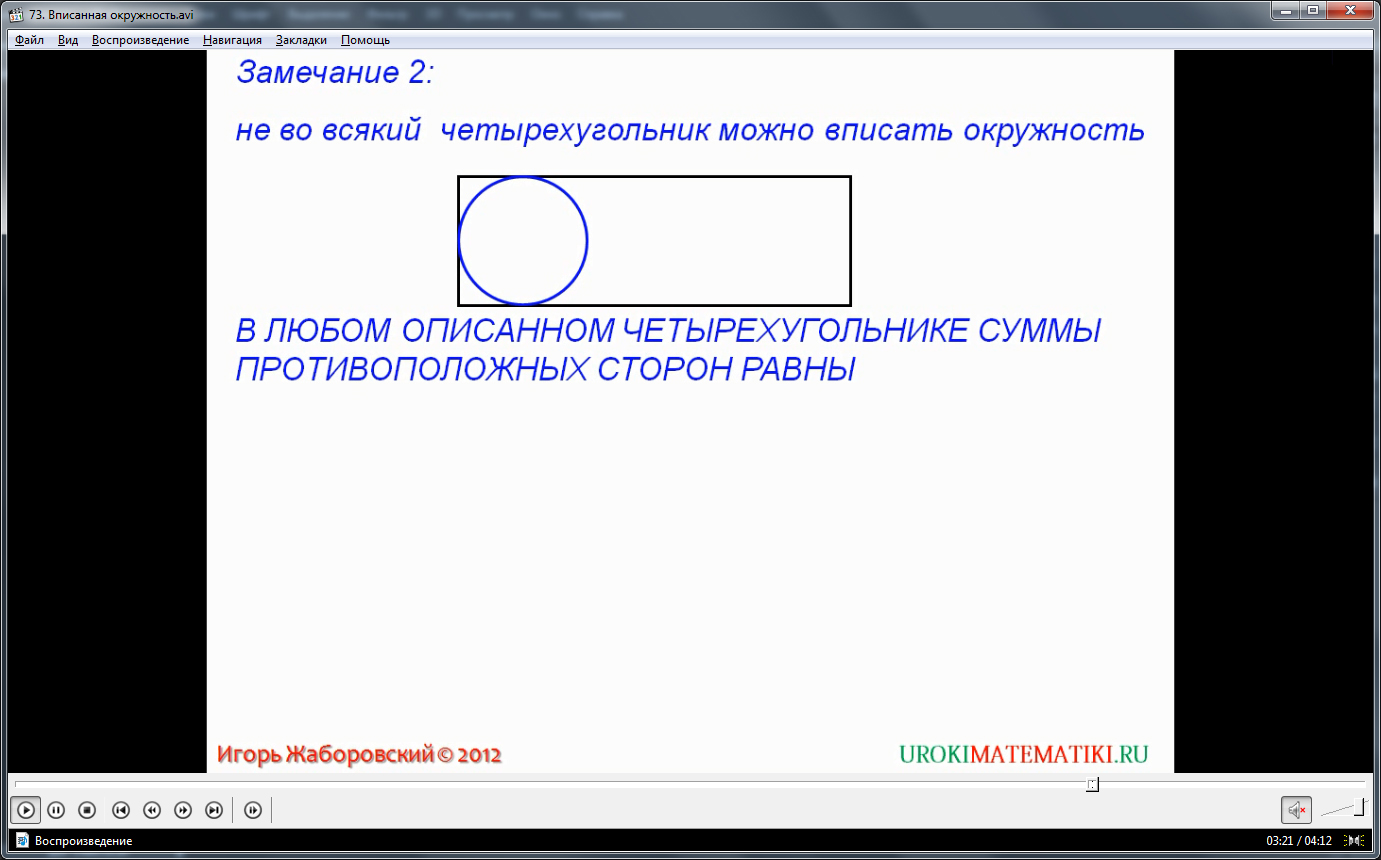
Вписанной в некий многоугольник, называется такая окружность, которая затрагивает каждую сторону многоугольника, в независимости от их количества. Соответственно, сам многоугольник называется, в данном случае, описанным вокруг окружности. Возможность вписывания зависит от параметров фигуры – например, в любой треугольник можно с легкостью вписать окружность, при этом существует только одна окружность для конкретно заданного треугольника. А вот многие неправильные и вытянутые многоугольники нельзя так просто описать вокруг окружности – как правило, на практике обычно окружность вписывается в правильные выпуклые симметричные многоугольники. Количество вершин и сторон не влияет на возможность вписать в фигуру окружность – решающую роль тут играют величины углов.
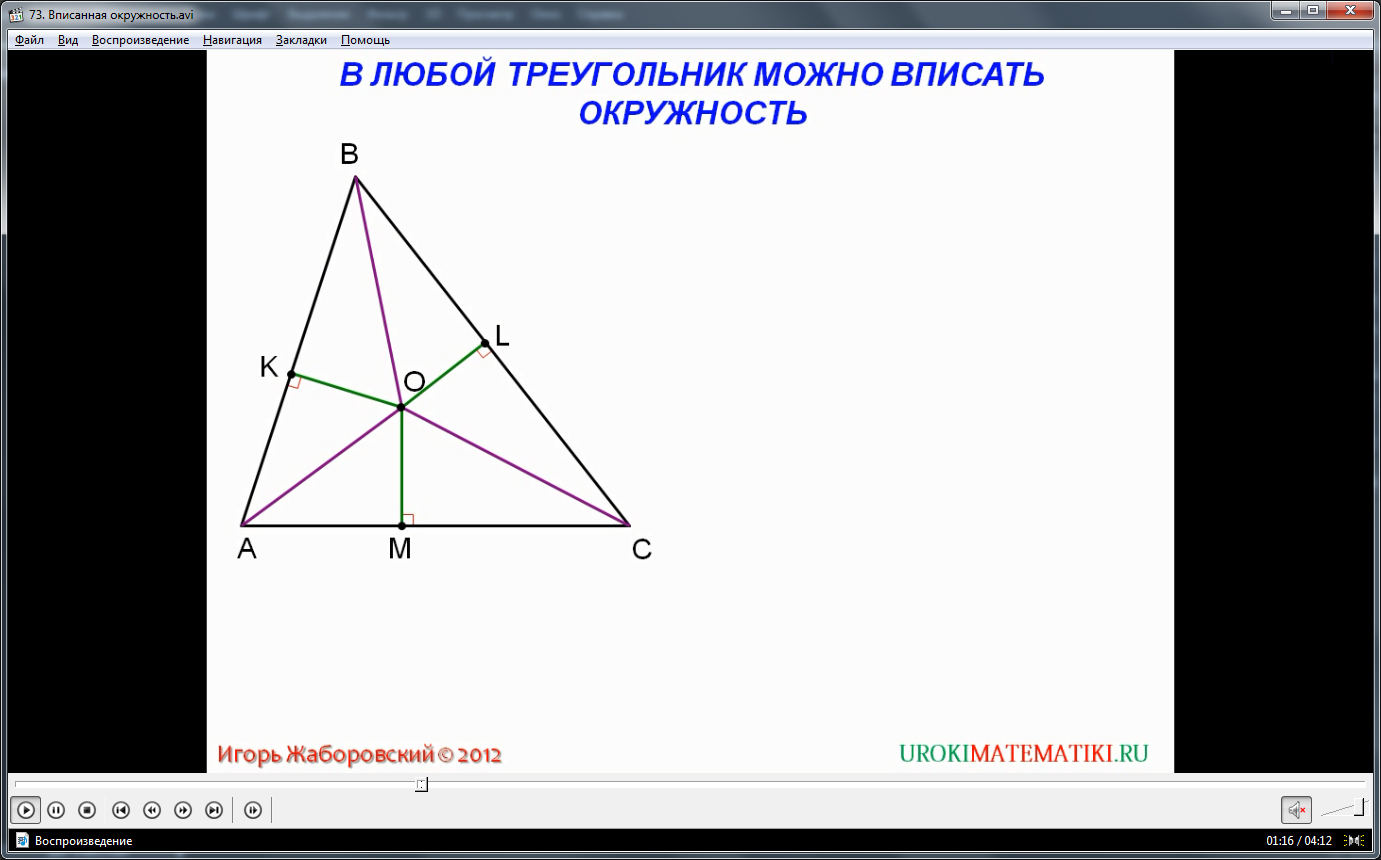
Зависимость от угловых значений проявляется в нескольких важнейших свойствах вписанных окружностей. Например, центр такой окружности является также точкой пересечения всех биссектрис, исходящих из каждого угла многоугольника. А суммы противоположных углов у многоугольника со вписанной окружностью равны между собой. Следствием из последнего свойства часто пользуются в обратном виде для нахождения ответа на вопрос: «Можно ли вписать окружность в данную фигуру?». Как видно в представленном видео, если суммы противолежащих углов равны между собой, в многоугольник можно легко вписать окружность - в противном случае, окружность будет вписана неполным образом – без затрагивания отдельных сторон.

Также важным критерием для правильного вписывания окружности в многоугольник служит отсутствие самопересечений – фигура должна быть выпуклой.
Проведем исследование одной из наиболее используемых теорем в данной области геометрии. Предположим, у нас есть некоторый четырехугольник АВСК, описанный вокруг окружности, с центром в точке О. При этом противоположные стороны четырехугольника не являются параллельными друг другу (это не разновидность трапеции или параллелограмма). Иначе говоря, АВ не параллельно СК, ВС не параллельно АК. Проведем две диагонали в нашем четырехугольнике, пусть это будут ВК и АС. Отрезки диагоналей разобьем пополам точками М и N, так что АМ = МС, ВN = NК.
Таким образом, точки М и N являются, соответственно, центрами диагоналей АС и ВК. Согласно теореме Ньютона, точки М, N и О лежат на одной, единственно определяемой прямой. Кроме того, дополняя выводами из теоремы Гаусса, можно сформулировать этот тезис следующим образом:
Середины всех диагоналей многоугольника лежат на одной прямой с точкой-центром вписанной окружности (если есть теоретическая возможность её вписать) и с серединой отрезка, соединяющего точки пересечения, продолжения сторон многоугольника. Прямая, на которой лежат все эти критические точки, именуется прямой Гаусса.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4990 |
| Номер материала | 611 |