
Урок «Формула суммы первых n членов геометрической прогрессии»

Краткое описание документа:
Видеоурок «Формула суммы первых n-членов геометрической прогрессии» представляет учебный материал в занимательной форме. В ходе данного видеоурока ученики знакомятся с формулой суммы членов геометрической прогрессии, учатся применять ее в решении практических задач. Цель данного видеоурока – наглядно представить информацию, повысить эффективность преподавания, освободить время учителя для индивидуальной и дифференцированной работы с учениками.

Видеоурок содержит иллюстрации, анимацию для представления в занимательной форме и удержания внимания учащихся. Для облегчения усвоения материала и его запоминания используются другие приемы – выделение цветом, рамкой и другими способами.
Урок начинается с представления темы и рассказа истории, в которой подчеркнуто, что знание математики может в жизни давать преимущества. Это история о шахе, которому мудрец подарил шахматы, и в награду попросил такое количество зерна, которое соответствовало бы сумме зерен, положенных на все клетки доски, где количество зерен на каждой следующей клетке было бы вдвое больше количества зерен на предыдущей клетке. После проведения подсчетов, шах с удивлением обнаружил, насколько огромно это число, и что дать такое количество зерна мудрецу невозможно. Ученикам демонстрируется проверка данной задачи. Напоминается, что данная последовательность является геометрической прогрессией со знаменателем 2 и первым членом 1. Сумма всех зерен будет составлять S=1+2+22+23+…+263. Предлагается умножить обе части равенства умножить на 2, после чего получится 2S=2+22+23+…+264. Вычтя из второго равенства первое, получим сумму 64-х членов последовательности S=264-1. Ученики с удивлением обнаруживают, что такое число составляет больше триллиона тонн зерна! Такое количество зерна человечество может собрать за тысячелетия.
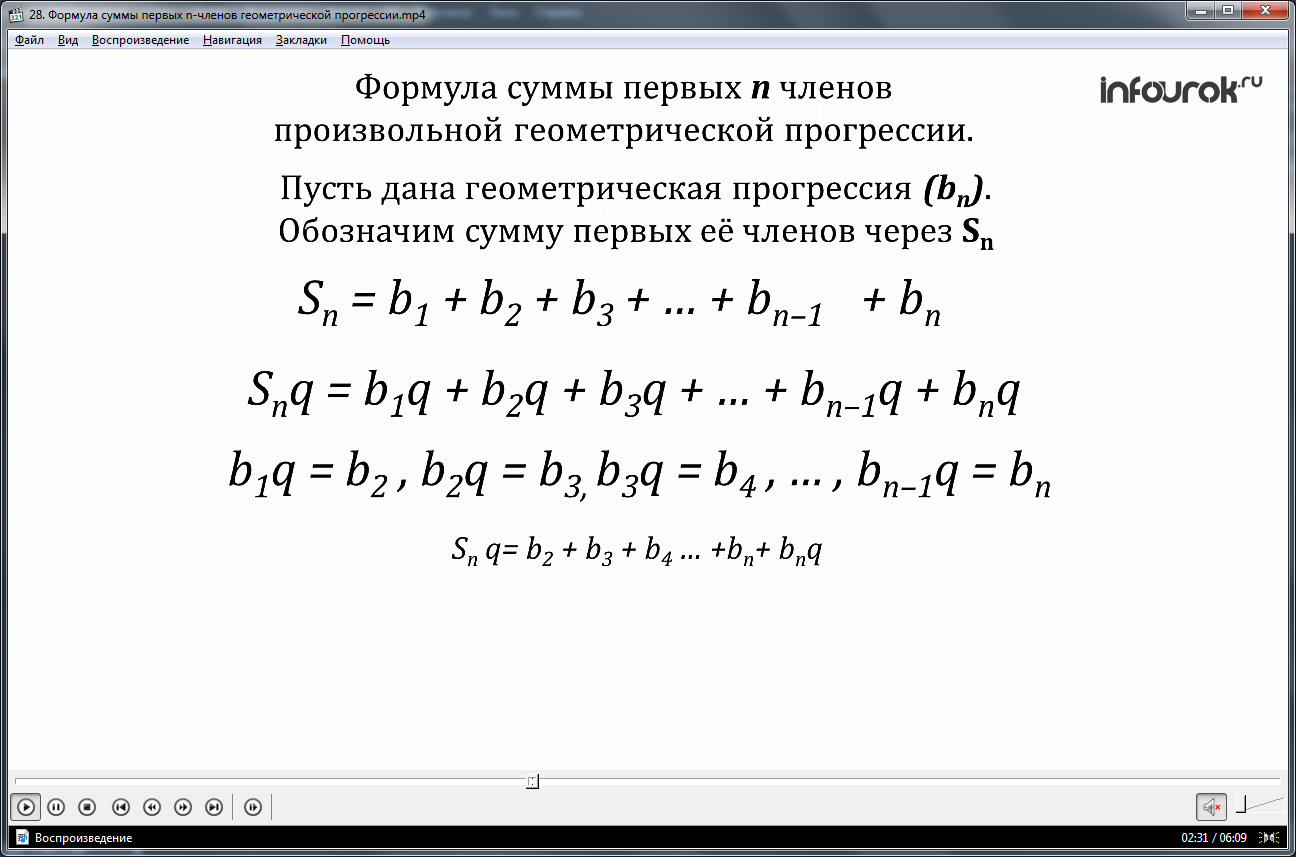
Аналогично рассуждениям вычисления количества зерна, положенного на шахматную доску, можно вывести общую формулу суммы некоторого числа n членов геометрической прогрессии (bn).Для этого обозначается сумма первых n членов как Sn=b1+b2+b3+b4+…+bn. При умножении всего ряда на число, равное знаменателю, получается Snq=b1q+b2q+b3q+b4q+…+bnq. При этом известно, что b1q=b2, b2q= b3, bn-qq=bn и т.д. Соответственно, формула суммы принимает вид Snq= b2+b3+b4+…+bnq. При вычитании из суммы Snq суммы Sn получается формула Sn(q-1)= bnq- b1. Для последовательности, в которой q≠1 формула принимает вид Sn=(bnq- b1)/(q-1).
Также выделяется частный случай, когда знаменатель прогрессии q=1. В этом случае сумма n членов прогрессии равна Sn=nb1. Представляется формула суммы n членов прогрессии в другом виде, который нередко применяется при решении задач. Указывается, что при замене bn соответствующим выражением b1qn для q≠1 будет верно Sn=b1(qn-1)/(q-1).
Предлагается рассмотреть решение примера, в котором b1=2, а q=1/2. Необходимо найти сумму 9 первых членов прогрессии. В решении задачи используется формула Sn=b1(qn-1)/(q-1), в которую подставляются значения первого члена и знаменателя. Вычислив значение, получаем S9=3+127/128.
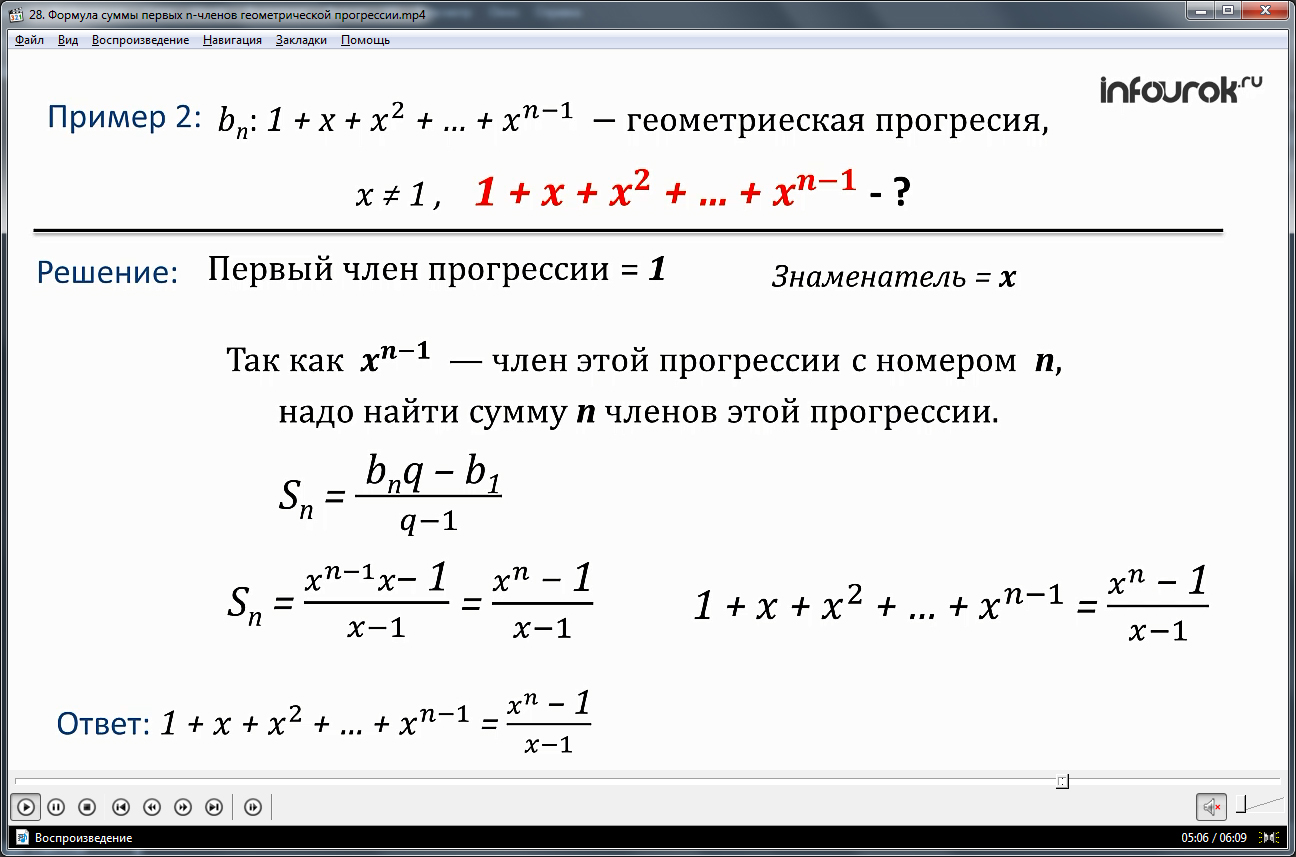
Рассматривается пример решения задачи, в которой необходимо найти сумму n членов прогрессии bn, определенной числами 1+х+х2+…+хn-1. Для проведения вычислений отмечаем, что первый член прогрессии b1=1, ее знаменателем является х. n-ным членом прогрессии является хn-1. Подставляем выражения, соответствующие первому и n-ному членам прогрессии в формулу Sn=(bnq- b1)/(q-1). Формула вычисления суммы n членов геометрической прогрессии принимает вид Sn=(xn-1)/(x-1). Значит, суммой прогрессии 1+х+х2+…+хn-1 будет Sn=(xn-1)/(x-1).
В третьем примере рассматривается решение задачи, в которой указаны некоторые члены геометрической прогрессии – b3=8 и b5=32, и необходимо вычислить сумму первых 8 членов. Для начала предлагается найти знаменатель прогрессии, зная 3 и 5 ее члены. Для этого пятый член представляется через третий: b5= b3q2. Из этой формулы следует, что q2= b5/b3=32/8=4. Ясно, что q может принимать значения 2 и -2. Для q=2 будет b1=2 и S8=510. Если же q=-2, то b1=2 и S8=-170.
Видеоурок «Формула суммы первых n-членов геометрической прогрессии» может служить наглядным материалом для проведения урока в школе. Также материал помогает освоить теоретическую часть и сформировать навыки решения задач по теме при дистанционном обучении и при самостоятельном рассмотрении
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8135 |
| Номер материала | 672 |