
Презентация "Определение синуса и косинуса на единичной окружности"

Краткое описание документа:
Данная презентация является очень полезной для каждого десятиклассника, который приступает к подробному изучению тригонометрии. Она рассчитана на учеников, которые заранее ознакомлены с тем, что такое числовая окружность. Без этого знания, они не смогут понять суть данной презентации.

Тригонометрия в целом является разделом в математике, который включает в себя изучение тригонометрических функций, а также, использование их в геометрии.
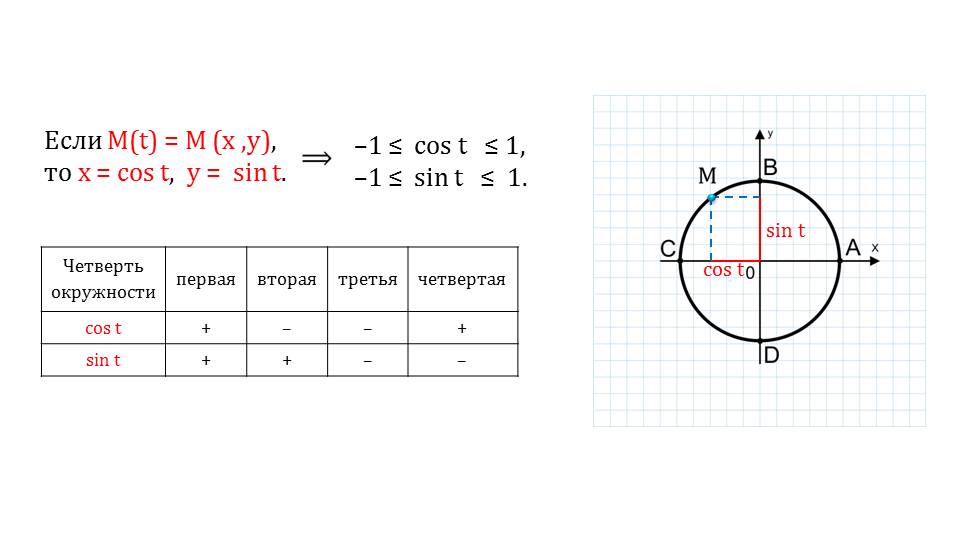
На первом слайде приводится иллюстрация единичной числовой окружности. Следовательно, радиус данной окружности равняется 1. Точки пересечения окружности с осями координат обозначены латинскими заглавными буквами A, B, C, D. В дальнейшем, они будут обозначаться таким образом. Мы видим, что на окружности выбрана произвольная точка M.
Данная точка имеет две координаты – значение абсциссы, значение аргумента. При этом абсцисса называется косинусом некоторого t, а ордината – синусом. На этом же слайде мы видим обозначения косинуса и синуса.
Это общепринятые символы, которые будут в дальнейшем довольно часто встречаться при изучении тригонометрии и в геометрии при решении задач. Таким образом, на оси ОУ мы будем искать синусы, а ось ОХ соответствует значение косинуса.


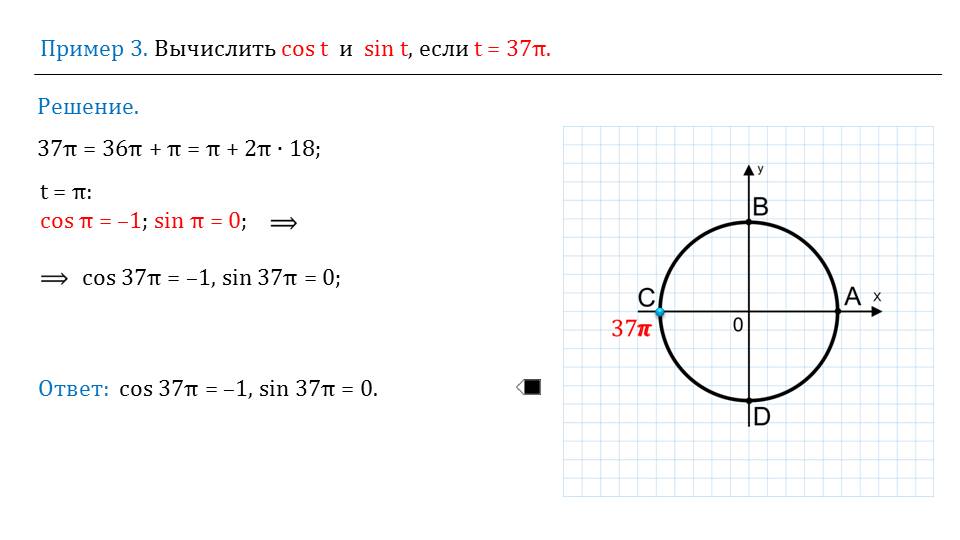
На следующем слайде указывается следующий момент – косинус и синус ограничены в интервале от -1 до 1. То есть, косинус некоторого числа не может быть меньше минус единицы или больше единицы. Аналогично и синус. Приведена таблица, на которой демонстрируется, какие знаки будут иметь косинус и синус в той или иной четверти. В этом можно легко убедиться, рассмотрев числовую окружность.

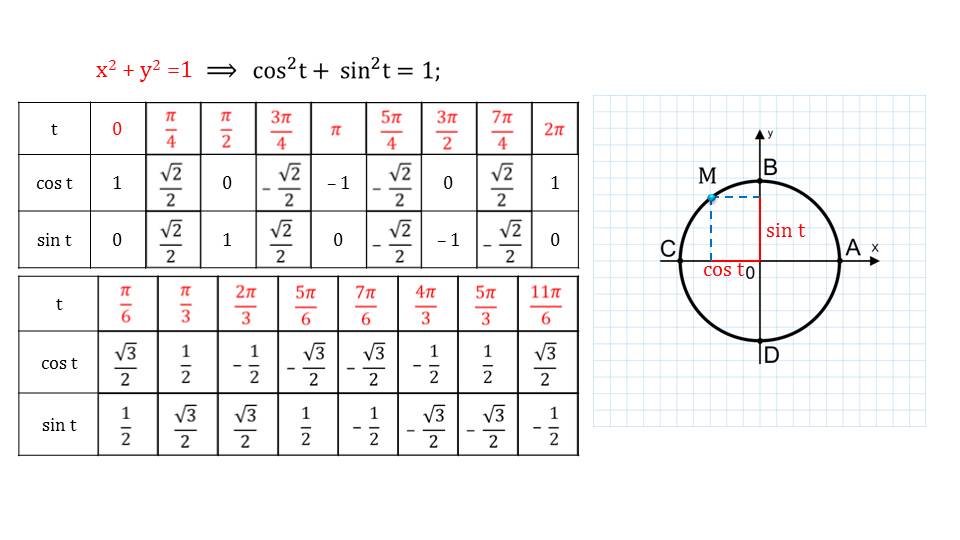
Далее указывается одно из важнейших и основных свойств тригонометрии. Согласно ему, сумма квадрата косинуса и синуса дает единицу. От данного свойства в дальнейшем будут возникать другие правила, которые охватываются тригонометрией. Получается основное свойство тригонометрии очень просто.
Ведь мы знаем, что уравнение единичной окружности представляется собой следующее равенство: сумма квадрата х и у равняется 1. Подставляя вместо х-а – косинус, а вместо у, соответственно синус, получим наше правило.


Это правило нужно записать в тетради и запомнить, как следует. С помощью него можно упростить в разы сложные выражения и уравнения в тригонометрии, которые возникают при решении различных задач.
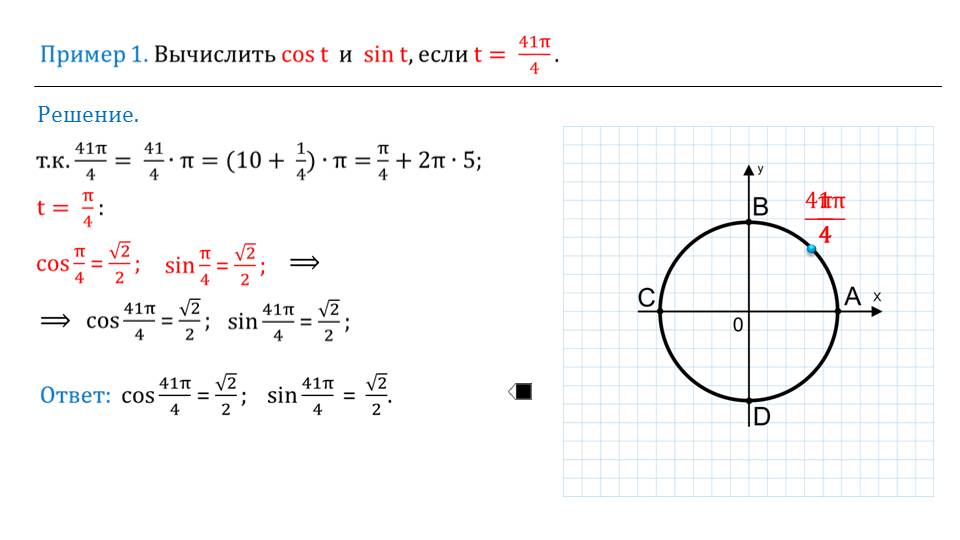
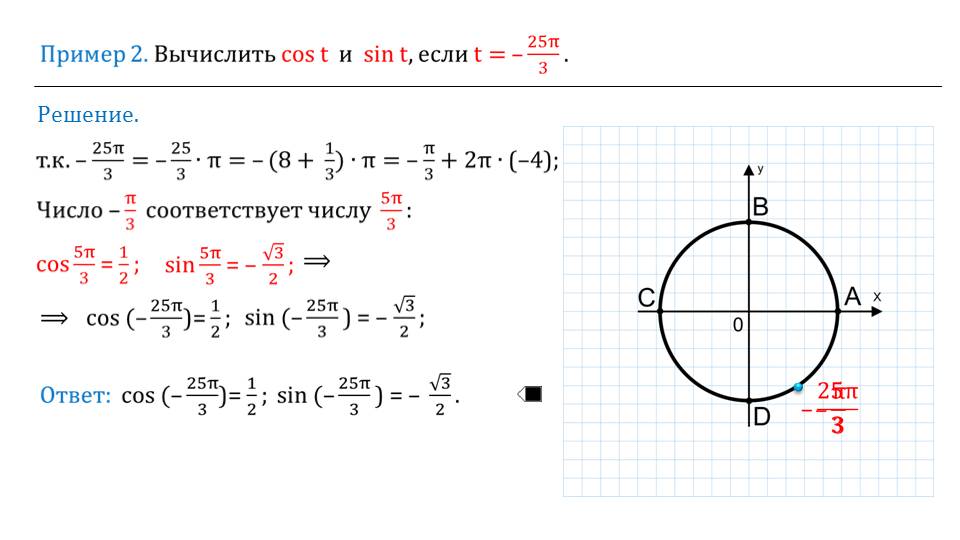
После этого предлагается решить 12 примеров, которые можно рассмотреть в классе вместе со всеми учениками и учителем, либо индивидуально. После просмотра, можно попробовать решить самостоятельно без подсказок, либо аналогичные иные примеры.

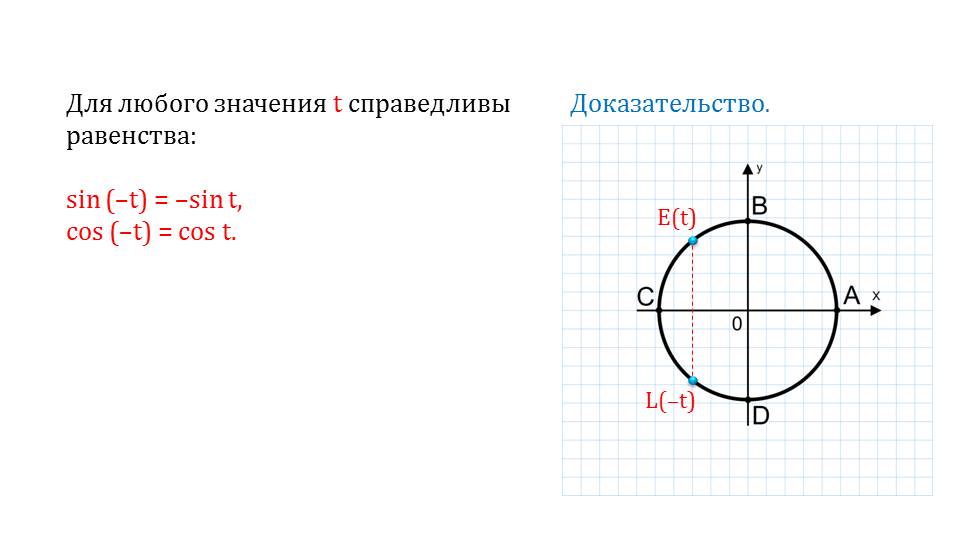
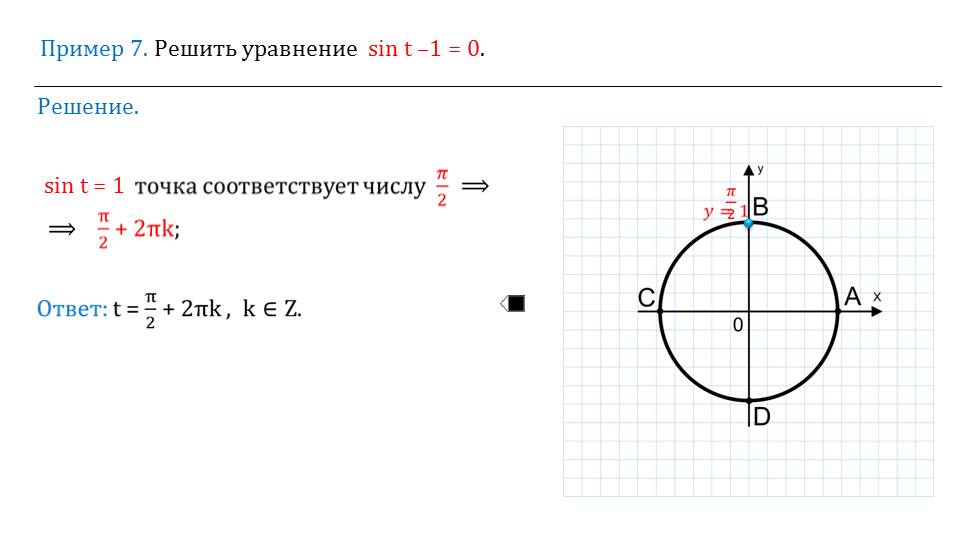
После того, как рассматривается большое количество примеров, которые, как следует, разъяснят все тонкости и помогут справиться с подобными задачами, продолжается дальнейшее объяснение темы. Указывается на то, что синус и косинус обладают периодичностью. Например, синус некоторого числа будет равняться синусу этого же числа с добавлением 2Пиk.

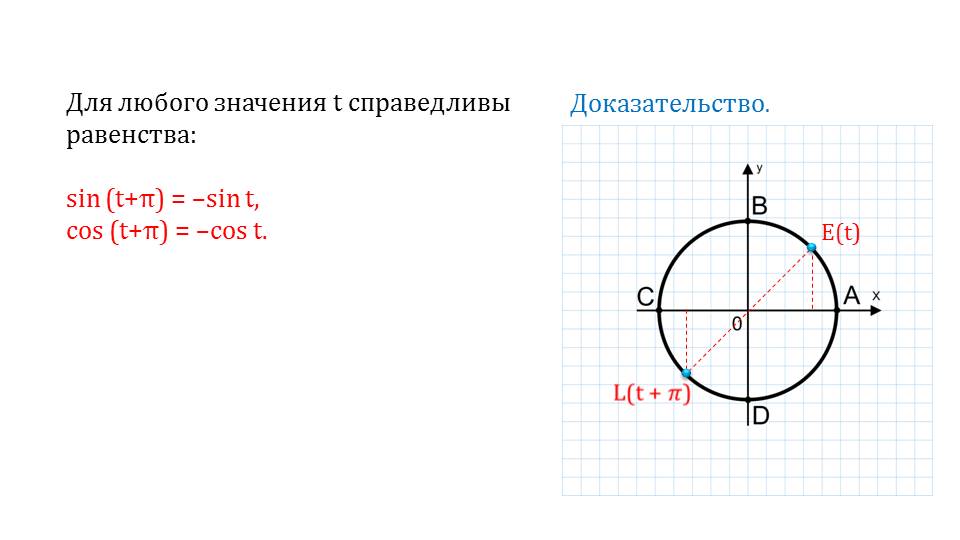
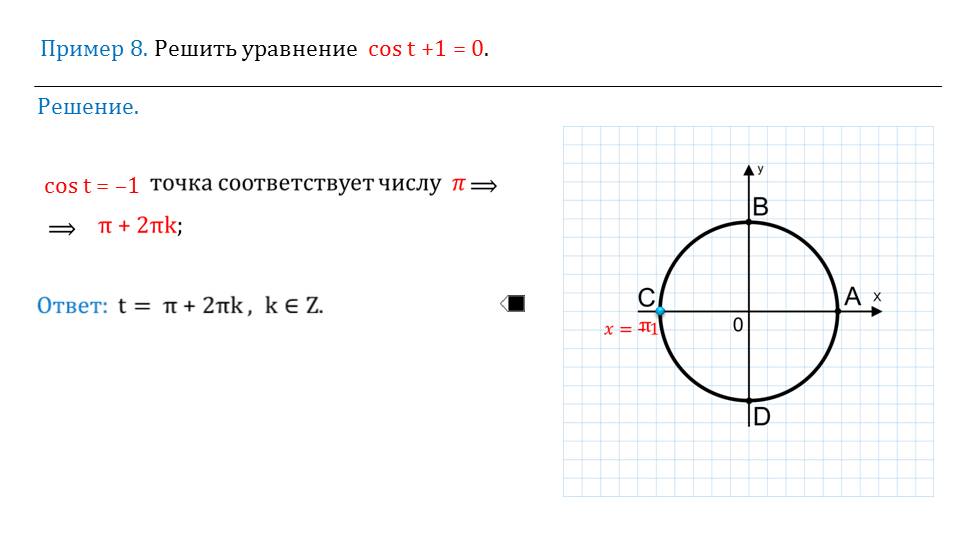
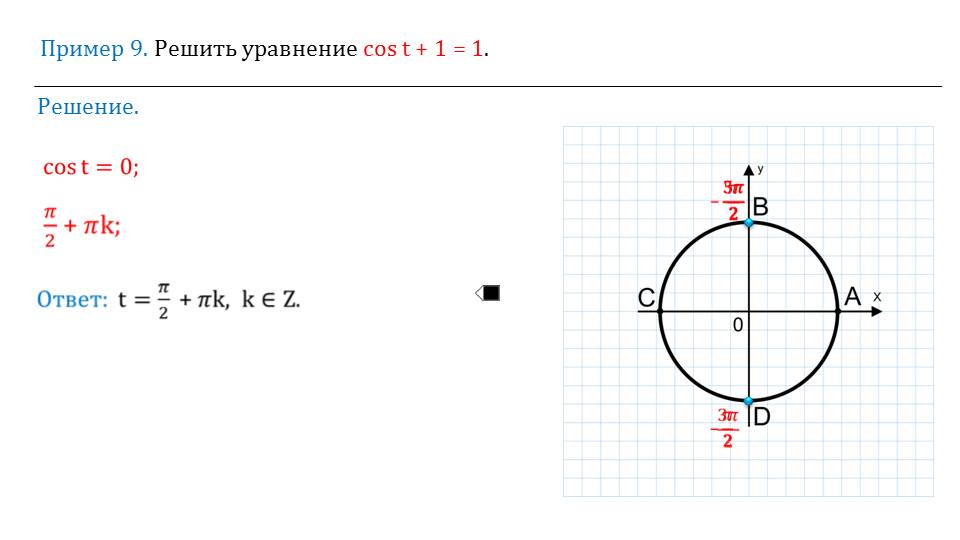
Зная знаки на той или иной четверти, можно записать и другие правила. Все они выводятся на последующих слайдах и обводятся в квадратные рамки. Это говорит о том, что стоит их запомнить с пониманием.

Начало тригонометрии не стоит пропускать. В дальнейшем все будет усложняться и углубляться. Эти знания понадобятся и помогут понимать лучше дальнейшее.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 8619 |
| Номер материала | 786 |