
Презентация "Функция y=cosx, ее свойства и график"

Краткое описание документа:
Одним из важных терминов в тригонометрии является косинус. В этой презентации будет рассматриваться функция косинуса, построен ее график. Подробно будут приводиться все свойства, которыми она обладает.

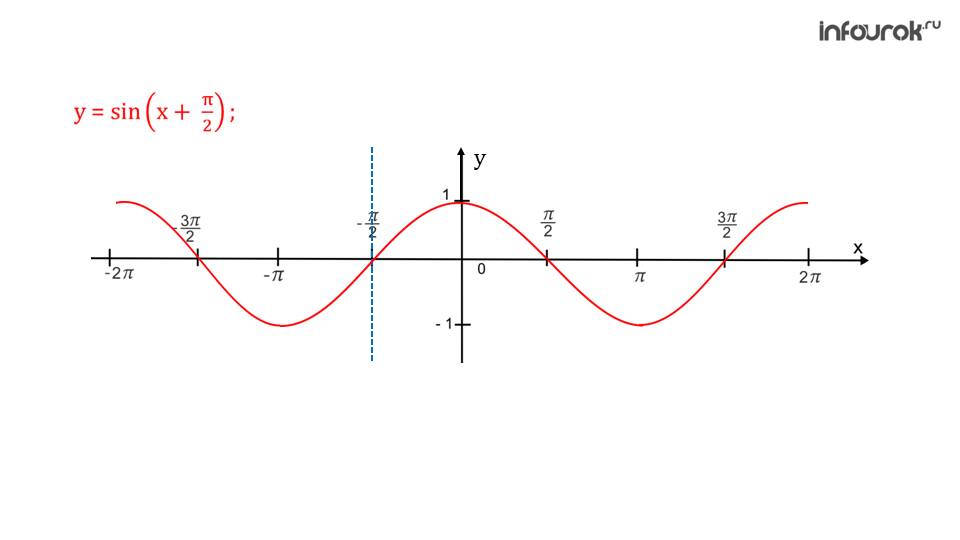
На первом слайде, прежде чем начать рассмотрение непосредственно функции, напоминается одна из формул приведения. Ранее она была подробно продемонстрирована вместе с доказательством.
Данная формула говорит о том, что функцию косину можно заменить синусом при определенных внесениях изменения в аргументе. Таким образом, уже изучив синусоиды, школьники смогу построить данную функцию. В результате они получат график функции косинуса.
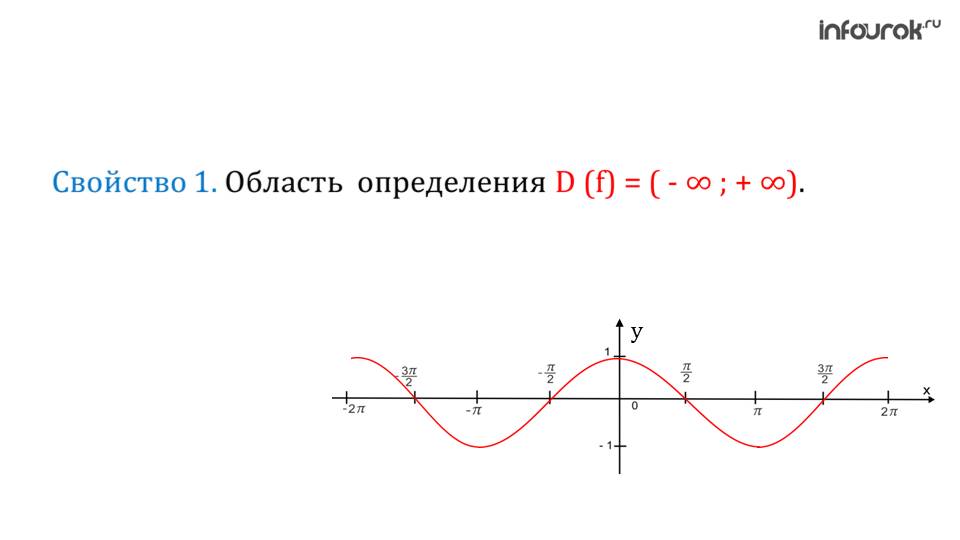
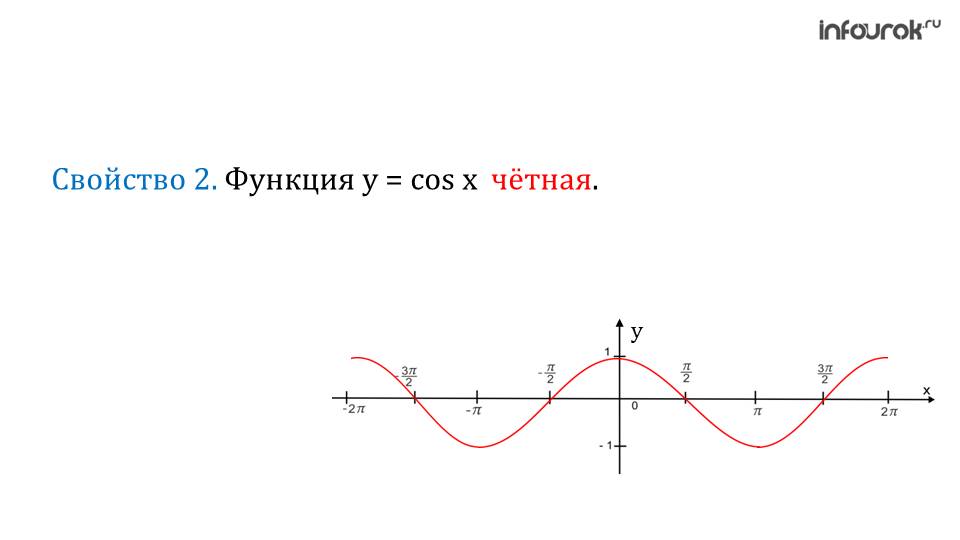
График функции можно увидеть на втором слайде. Можно обратить внимание, что синусоида лишь сместилась на Пи/2. Таким образом, в отличие от синусоиды, график функции косинуса не проходит через точку (0;0).
Первым делом стоило бы рассмотреть область определения функции. Это важный момент и с этого начинается анализ любой функции в математике. Областью определения данной функции является вся числовая ось. Это отчетливо видно на графике функции.
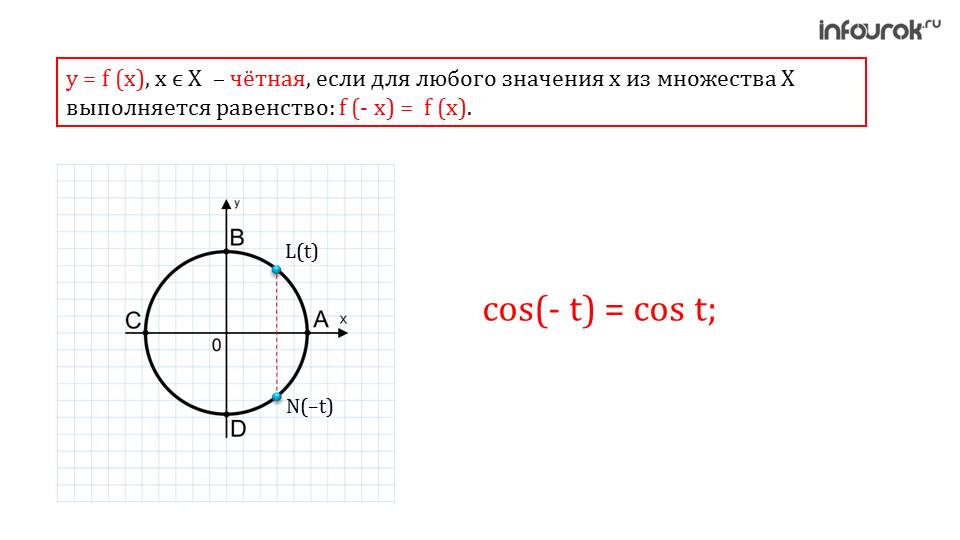
В отличие от синуса, функция косинуса является четной. То есть, если изменить знак аргумента, знак функции не изменится. Четность же обуславливается свойством синуса.
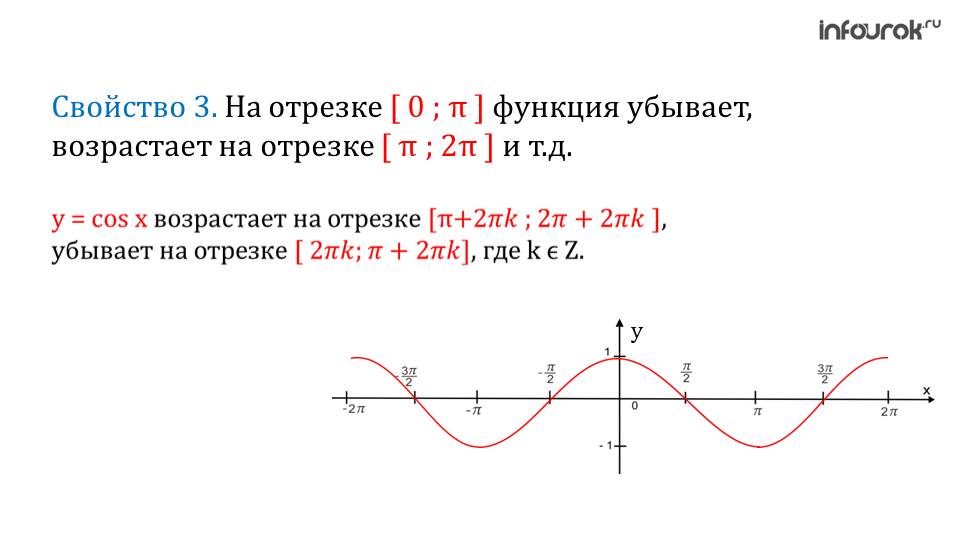
На определенных интервалах функция возрастает, на определенных – убывает. Это говорит о том, что функция косинуса является монотонной. Данные интервалы показаны на следующем слайде. На графике наглядно можно увидеть возрастание и убывание функции.
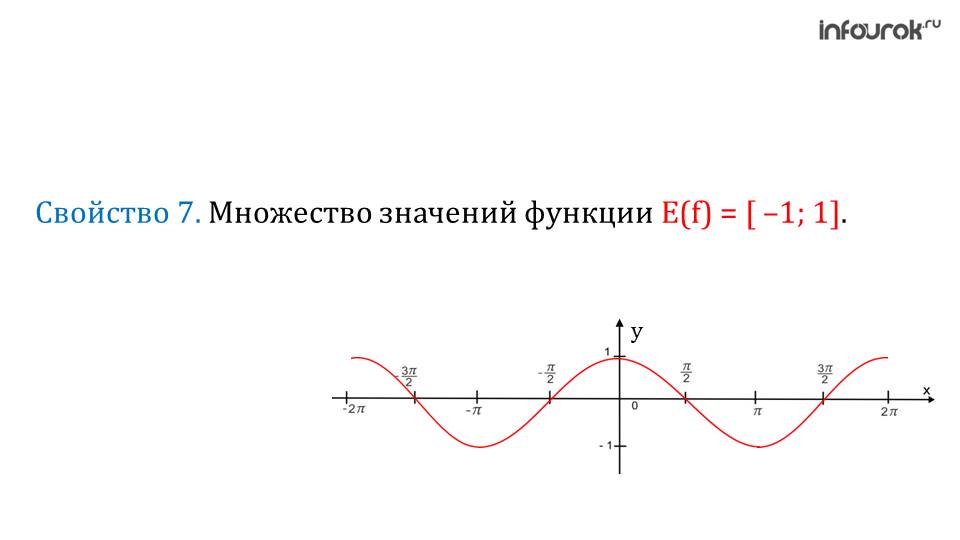
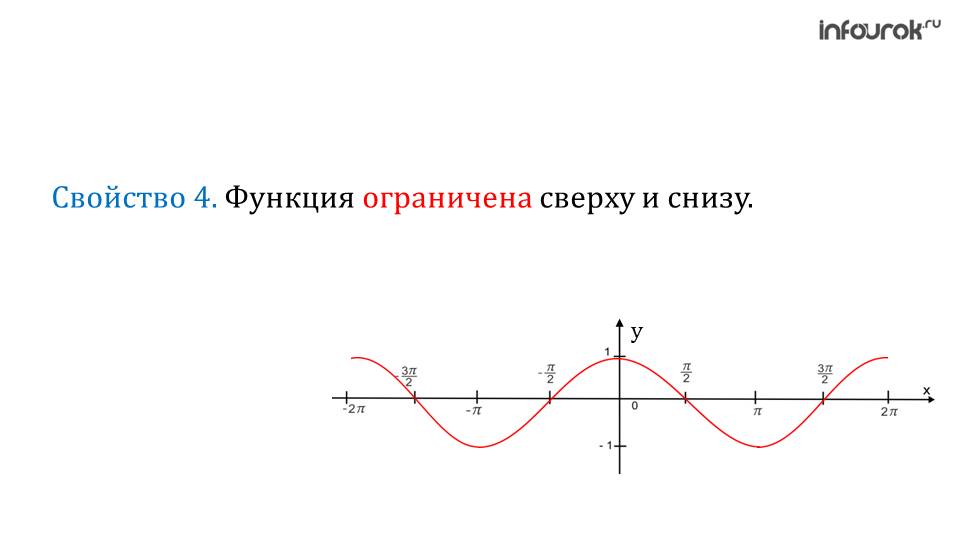
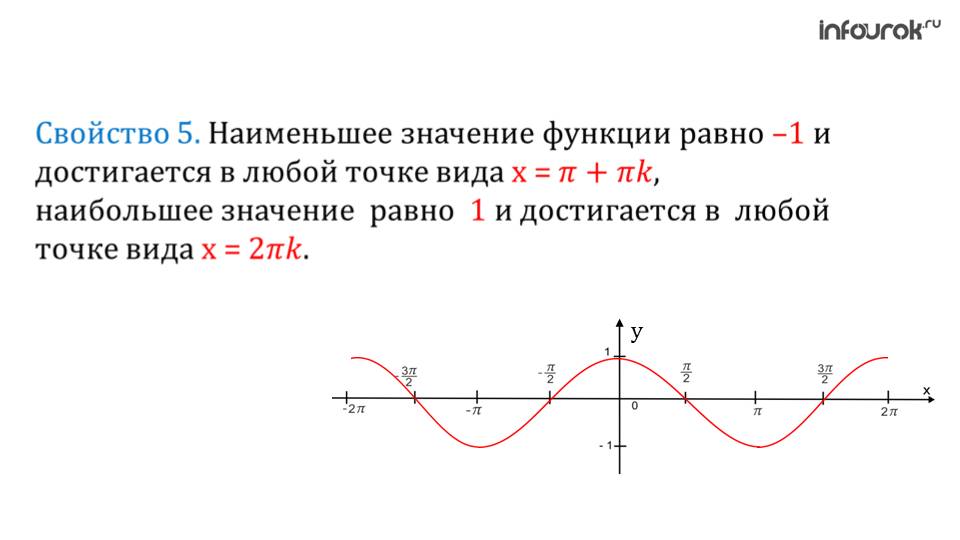
Пятое свойство – это ограниченность. Функция косинуса имеет ограниченность и сверху, и снизу. Минимальным значением является -1, а максимальным -+1.
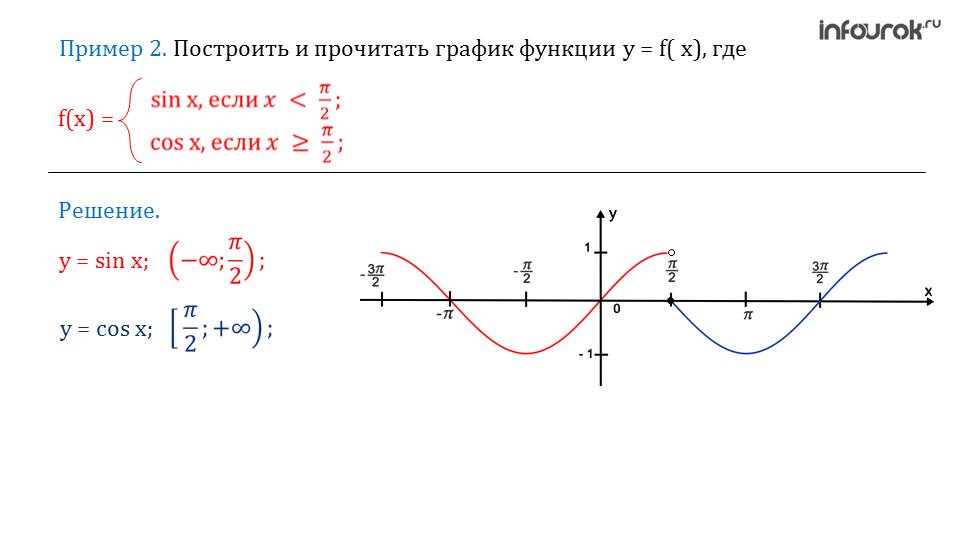
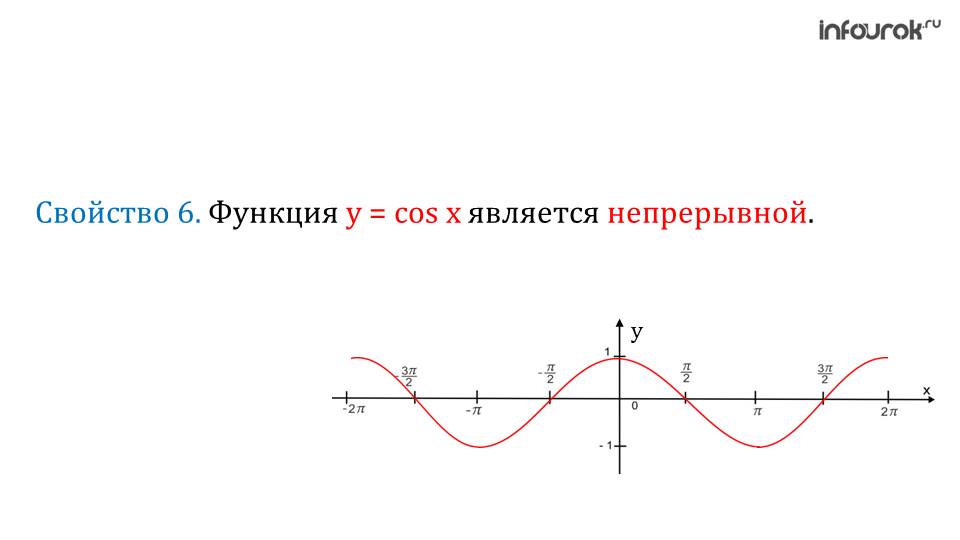
Так как нет точек разрыва и острых пиков – функция косинуса, как и функция синуса, является непрерывной.
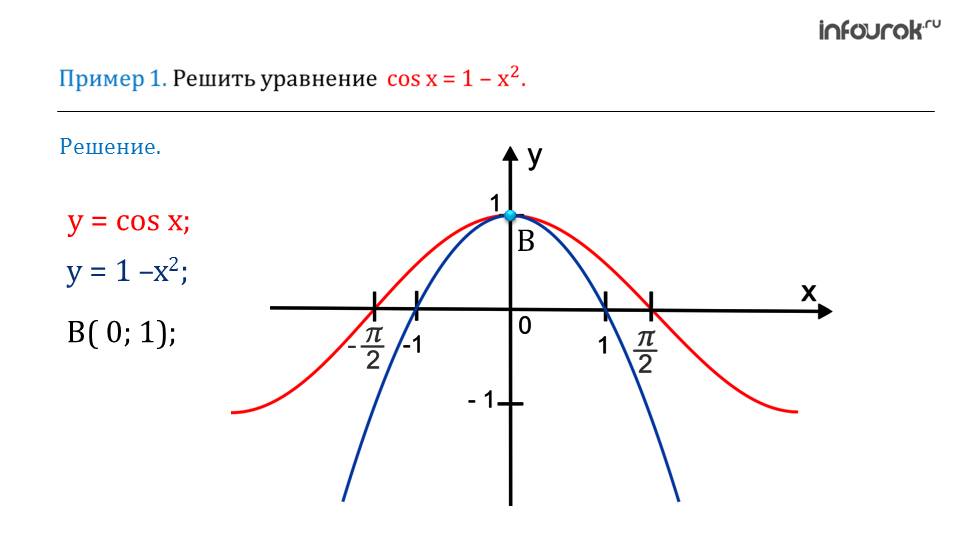
Далее выводится множество значений, которые может принимать функция. После этого показываются примеры, при решений которых используется графический метод.
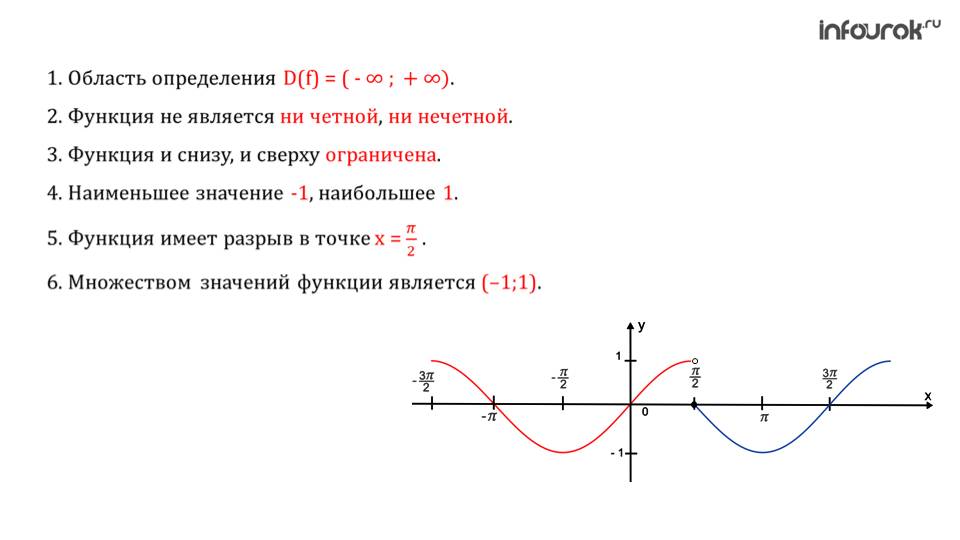
На последнем слайде демонстрируется обобщенно все свойства, которые были рассмотрены в презентации. Это ряд основных характеристик, которыми обладает функция косинуса. Запомнив их, можно с легкостью справиться с рядом уравнений, которые содержат косинус. Проще всего будет освоить данные свойства в случае полнейшего понимания сути.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 9081 |
| Номер материала | 794 |