
Презентация "Медианы, биссектрисы и высоты треугольника"

Краткое описание документа:
В данном уроке речь пойдёт о медиане, биссектрисе и высоте треугольника. Именно здесь учащиеся подробнее познакомятся с трема важными элементами изучаемой нами фигуры.
Слова достаточно новые для данного раздела математики, поэтому порой стоит использовать стихотворение о медиане, где она сравнивается с обезьяной, у которой очень зоркий глаз, почему она и прыгает точно на середину противоположной стороны. Шуточное запоминание о биссектрисе сравнивает её с крысой, которая каким-то образом бегает по углам, а дальше делит их пополам. Такие стихотворения помогаю учащимся проводить ассоциативный ряд с новыми определениями и запомнить смысл определения лучше. Именно поэтому необходимо использовать такие легко рифмующиеся строчки. Про высоту треугольника стихотворений не написано, потому что она не обладает уникальными характеристиками в сравнении с другими фигурами.

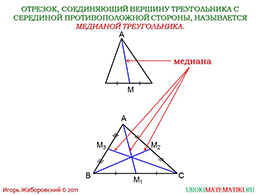
слайды 1-2 (Тема презентации "Медианы, биссектрисы и высоты треугольника", определение медианы)
Перед нами треугольник с вершиной «А». Сделаем следующее соединение: проведём линию от вершины к точке «М». Полученная точка «М» - середина противоположного отрезка. Новый отрезок «АМ» носит специальное название - медиана. Дадим строгое определение. Отрезок, который соединяет вершину треугольника с серединой противоположной стороны фигуры, называется медианой треугольника. Дефиницию мы разобрали, но у нашей фигуры ведь три вершины: «А», «В», «С», поэтому получается и три середины: «М1», «М2», «М3». В результате количество медиан следующее: «АМ1» - одна медиана, «ВМ2» - вторая медиана, «СМ3» - третья медиана. Получается, у каждого треугольника в любом случае будет три медианы.
Все три медианы остроугольного, тупоугольного или прямого треугольника будут пересекать в определённой точке, а эта точка обладает замечательными свойствами. И вот мы дали определение медианы и показали, что треугольнику обязательно наличие трёх медиан.
слайды 3-4 (определение биссектрисы, определение высоты)
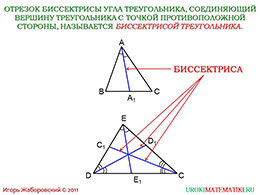
Теперь поговорим о другой фигуре или важном элементе изучаемой фигуры: биссектрисе. Вот треугольник «АВС», мы видим, что у него есть три угла: «А», «В» и «С». При вершине «А» угол имеет биссектрису «АА1». Если говорить о биссектрисе угла, то она является лучом, а отрезок в границах треугольник - биссектриса треугольника. То есть в нашем случае отрезок «АА1» является частью биссектрисы. Теперь дадим строгое определение изучаемому термину. Отрезок биссектрисы угла, который лежит в рамках треугольника, называется биссектрисой треугольника.
На рисунке мы видим биссектрису, которая соответствует первой вершине, но у треугольника три вершины. Допустим треугольник «DEC». «ЕЕ1» - одна биссектриса, «DD1» - другая биссектриса, «СС1» - третья биссектриса. Все они рассекают углы пополам. Выясним далее, что все три биссектрисы любого треугольника пересекаются в одной точке – важное свойство.
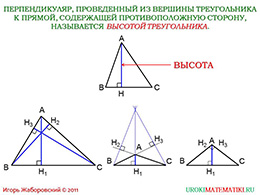
Ещё один элемент треугольника – его высота. Вот наша фигура «АВС», где прямая «ВС» лежит на стороне. Также есть точка «А», которая не лежит на прямой. Мы знаем, что из точки «А» можно построить единственный перпендикуляр «АН» на «ВС». Этот перпендикуляр и называется высотой. Теперь строгое определение. Перпендикуляр, который проведён из вершины на противоположную сторону, называется высотой треугольника. И вот, мы теперь знаем, что такое высота треугольника, но какое количество высот возможно у нашей фигуры? По три! Мы видим, что у треугольника «АВС» «НН1» - первая высота, «ВН2» - вторая высота, «СН3» - третья высота. В дальнейшем мы выясним, что все эти три высоты пересекаются в одной точке. Это происходит в любом треугольник: остроугольном, тупоугольном, прямоугольном. В нашем случае эта точка находится внутри треугольника, однако она может находиться и за его пределами (например, в тупоугольном треугольнике).
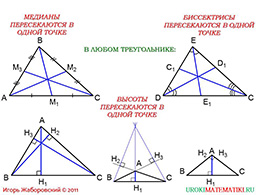
слайд 5 (примеры)
Теперь поговорим о другой фигуре или важном элементе изучаемой фигуры: биссектрисе. Вот треугольник «АВС», мы видим, что у него есть три угла: «А», «В» и «С». При вершине «А» угол имеет биссектрису «АА1». Если говорить о биссектрисе угла, то она является лучом, а отрезок в границах треугольник - биссектриса треугольника. То есть в нашем случае отрезок «АА1» является частью биссектрисы. Теперь дадим строгое определение изучаемому термину. Отрезок биссектрисы угла, который лежит в рамках треугольника, называется биссектрисой треугольника.
На рисунке мы видим биссектрису, которая соответствует первой вершине, но у треугольника три вершины. Допустим треугольник «DEC». «ЕЕ1» - одна биссектриса, «DD1» - другая биссектриса, «СС1» - третья биссектриса. Все они рассекают углы пополам. Выясним далее, что все три биссектрисы любого треугольника пересекаются в одной точке – важное свойство.
Ещё один элемент треугольника – его высота. Вот наша фигура «АВС», где прямая «ВС» лежит на стороне. Также есть точка «А», которая не лежит на прямой. Мы знаем, что из точки «А» можно построить единственный перпендикуляр «АН» на «ВС». Этот перпендикуляр и называется высотой. Теперь строгое определение. Перпендикуляр, который проведён из вершины на противоположную сторону, называется высотой треугольника. И вот, мы теперь знаем, что такое высота треугольника, но какое количество высот возможно у нашей фигуры? По три! Мы видим, что у треугольника «АВС» «НН1» - первая высота, «ВН2» - вторая высота, «СН3» - третья высота. В дальнейшем мы выясним, что все эти три высоты пересекаются в одной точке. Это происходит в любом треугольник: остроугольном, тупоугольном, прямоугольном. В нашем случае эта точка находится внутри треугольника, однако она может находиться и за его пределами (например, в тупоугольном треугольнике).
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6634 |
| Номер материала | 242 |