
Презентация "Второй признак равенства треугольников"

Краткое описание документа:
Теперь поговорим о нашей теме: схожесть или, как более корректно сказать, равенство треугольников. Что это означает? Получается, что такие треугольники совмещаем наложением, а за этим действием потянется равенство всего: вершин, сторон и углов. Вот что следует из равенства данной основополагающей в геометрии фигуры. Наша ближайшая задача – доказать второй признак равенства треугольников.
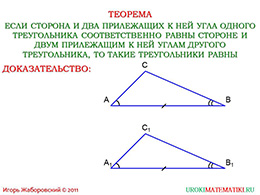
слайды 1-2 (Тема презентации "Второй признак равенства треугольников", теорема)
Обратим внимание на формулировку теоремы, которая изображена на доске. Получается, что мы анализируем признак по двум углам и стороне между ними. Сколько в целом таких теорем? О чём была первая? Теперь вернёмся к доказательству нашей теоремы способом совмещения.
Итак, у нас есть два треугольника, в которых «АВ» равняется «А1В1», угол «А» равняется углу «А1», а угол «В» равняется углу «В1». Необходимо доказать, что именно эти треугольники являются равными. Отрезки равны, потому что их можно совместить наложением. Также мы накладываем прилежащие углы. Осталось понять, что совместятся точки «С» и «С1». Точка «С» - это пересечение двух лучей: «АС» и «ВС», значит точка «С1» является пересечением лучше «А1С1» и «В1С1». Если мы совместили одну сторону и прилежащие два угла, то оставшиеся отрезки и вершина также совместятся. Таким образом, треугольники равны. Что и требовалось доказать.
В завершении необходимо подытожить весь теоретический материал, чтобы учащиеся могли его использовать при решении типовых задач. Треугольник – геометрическая фигура, но что означает равенство таких фигур? Мы должны суметь сопоставить фигуры наложением, тогда они и будут равными. Уточните у учащихся, как мы можем осуществить это наложение (визуально или зная определённые признаки). Повторите формулировку второго признака.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5439 |
| Номер материала | 244 |