
Презентация "Графическое решение квадратных уравнений"

Краткое описание документа:
Презентация на тему «Графическое решение квадратных уравнений» является прекрасным наглядным пособием, которое поможет учителям в легкой и доступной форме объяснить ученикам различные методы решения квадратных уравнений графическим способом. Для наиболее четкого восприятия учениками, каждый слайд презентации сопровождается подробным описанием одного из способов решения уравнения и четкими графическими изображениями с пояснениями. Презентация имеет строгую и логичную структуру. Примеры в ней расположены по мере усложнения, что позволяет правильно построить учебный процесс и дать учащемуся возможность овладеть навыками решения квадратных уравнений графическим способом в полной мере.

слайды 1-2 (Тема презентации "Графическое решение квадратных уравнений", пример)
После названия презентации следует слайд, на котором представлено определение квадратного уравнения и дана его общая формула. Данный слайд дает понять, что коэффициенты, стоящие перед знаком переменной могут являться любыми числами, за исключением коэффициента, стоящего перед переменной величиной, находящейся под знаком квадрата, который ни в коем случае не может быть равен нулю.
Знание общего определения квадратного уравнения необходимо ученику, так как только в этом случае, он сможет правильно идентифицировать его, отличив от огромного количества других уравнений, и не ошибиться в принятии решения о том, каким способом осуществить поиск решений уравнения. Также графический рисунок дает понять, что в графическом изображении квадратное уравнение представляет собой параболу.
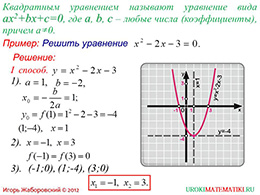
Далее на сайте демонстрируется пример решения простейшего квадратного уравнения первым способом. Пользуясь данным слайдом, учитель сможет подробно и понятно объяснить ученикам последовательность решения квадратного уравнения первым способом, начиная от нахождения коэффициентов, стоящих перед знаком переменной, с помощью которых, используя определенные формулы, находится вершина параболы, а корни уравнения определяются как абсциссы точек, в которых парабола пересекает ось.
слайды 3-4 (примеры)
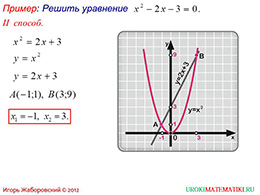
Третий слайд презентации показывает способ решения уравнения, описанного на предыдущем слайде, только другим методом. Данный способ имеет следующий смысл: уравнение предлагается разбить на две части, левая часть которого содержит переменную величину в квадрате, а правая представляет собой обычную прямую. Для осуществления поиска решений уравнения, необходимо построить оба графика, первый является параболой, а второй прямой линией, и определить координаты точек, в которых они пересекаются, значения которых и будут являться решениями данного уравнения.
Справа от подробно разобранного примера представлено само графическое решение квадратного уравнения, на котором четко подписаны все графики и обозначены точки, что позволяет ученику без проблем овладеть вторым графическим методом решения квадратного уравнения.
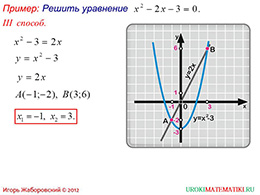
На четвертом слайде представлено описание третьего способа решения квадратного уравнения графическом способом. Данный способ очень напоминает по своей структуре метод, описанный на предыдущем слайде. Различие заключается в том, что ученикам предлагается построить два графика, один из которых будет представлять собой смещенную вверх или вниз по оси ординат параболу, а другой будет представлять собой прямую, проходящую через начало координат.
Корни уравнения также определяются по точкам пересечения двух графиков, аналогично предыдущему способу. Как и в предыдущих вариантах, справа от разобранного примера имеется графическое решение, все линии и графики изображены разными цветами, что позволяет учащемуся с легкостью овладеть данным способом решения уравнения.
слайды 5-6 (примеры)
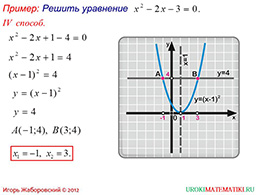
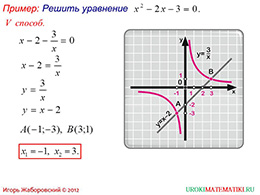
Как было сказано выше, каждый из слайдов описывает отдельный способ решения квадратного уравнения графическим способом, а презентация составлена так, что сначала идут более легкие примеры, которые затем усложняются. Пятый слайд предлагает учащимся разобраться с четвертым способ решения квадратного уравнения, который заключается в том, что коэффициент C, не имеющий при себе переменной величины, раскладывается на два числа, сумма или разность которых представляют собой коэффициент C без каких-либо изменений. Данные числа подбираются таким образом, чтобы одна из частей уравнения могла быть преобразована по формуле полного квадрата. Далее старятся графики обоих сторон уравнения, при этом правая часть представляет собой смещенную влево или вправо параболу, а левая часть является прямой линией, которая параллельна горизонтальной оси. Решение уравнения находятся аналогичным образом : как координаты точек в которых пересекаются график параболы и график прямой линии.
Заключительный пятый способ, который представлен на шестом слайде, является наиболее сложным для понимания, но не менее эффективным. Данный метод предполагает избавление от переменной величины, стоящей под знаком квадрата, путем деления всех членов уравнения на эту переменную величину. В результате данных преобразований получается следующее: одна из частей является графиком, описывающим прямую линию, а другая часть представляет собой график гиперболы. Для осуществления поиска решений, учащимся необходимо построить оба графика и найти координаты точек пересечения. Применение этого метода будет возможным только тогда, когда свободный коэффициент не является нулем, в противном случае, данный способ не применим. Подробно разобранный пример и наглядное графическое пояснение, расположенное с правой стороны от него, дают ученику возможность овладеть последним пятым способом решения квадратных уравнений графическим способом, без особых проблем и затруднений.


слайды 7-8 (примеры)
Следующие слайды являются обобщением всех предыдущих. На них в общих словах, уже без примеров, описывается каждый из способов решения квадратного уравнения графическим способом в общем виде, что дает возможность ученикам, освоив каждый из способов на конкретном простейшем примере, в дальнейшем применять их для решения более сложных квадратных уравнений.
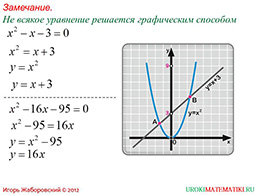
На этом данная презентация не заканчивается. Для того, что бы учитель мог объяснить учащимся, что не каждое квадратное уравнение может быть решено графическим способом, представлен последний – девятый слайд. На нем рассмотрено несколько примеров уравнений, решение которых не может быть осуществлено с применением вышеизложенных данных. Так, первый пример и описывающий его графический рисунок, показывают учащемуся, что, в связи с тем, что корни квадратного уравнения не всегда являются целыми числами, то правильно определить их по графику становится весьма затруднительно, а в некоторых случаях и невозможно.
Другой пример, показанный на данном слайде, призван объяснить, что порой применять один из вышеописанных методов решения - нецелесообразно. Чаще всего это возникает в том случае, если коэффициенты уравнения представляют собой достаточно большие числа, что затрудняет процесс построения графиков и выбора масштаба.
слайд 9 (замечание)
Данная презентация может быть использована в качестве учебного материала, как в пределах школы, так и рекомендована учащимся для самостоятельного освоения темы. Показ презентации можно осуществлять с помощью специального оборудования, в связи с тем, что вся информация представлена четко и ярко и качество графических изображений подобрано таким образом, чтобы вся представленная информация было хорошо видна учащимся во всем классе.
Презентация « Графическое решение квадратных уравнений» является отличным наглядным пособиям, позволяет оптимизировать и ускорить процесс обучения и донести до учащихся информации более новым и интересным интерактивным способом, нежели использование доски и мела. Плюсом использования интерактивного материала является также то, что при необходимости можно в любой момент вернуться к любому предыдущему слайду, осуществив лишь несколько простых движений, и не имея необходимости заново воспроизводить стертые с доски примеры, и еще раз объяснить ученикам информацию, которую они не поняли.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4926 |
| Номер материала | 297 |