
Презентация "Формулы корней квадратных уравнений"

Краткое описание документа:
Презентация на тему «Формулы корней квадратных уравнений Часть 1» является отличным учебным пособием, в котором представлен весь основной материал, необходимый для успешного освоения темы «Формулы корней квадратного уравнения», применение которого на ранних стадиях изучения методов поиска корней квадратных уравнений, даст отличные результаты. Презентация предназначена для использования учителями в средней школе и нацелена на оптимизацию учебного процесса.
Использование данной презентации позволит в легкой и доступной форме преподнести учащимся основные формулы и правила, необходимые для решения квадратных уравнений. Презентация «Формулы корней квадратных уравнений Часть 1» имеет четкую и логичную структуру, весь материал изложен именно в той последовательности, которая необходима для полного овладения темой.
Примеры в презентации представлены по мере их усложнения, что позволяет, овладев навыками решения простейших уравнений применять полученные знания для решения гораздо более сложных уравнений. Использование учителем математики данной презентации на уроке значительно повысит интерес учащихся к изучаемому материалу, ведь школьникам данной возрастной категории необходимо предлагать новые и интересные методы преподнесения материала, и, как следствие, повысит степень усвоения новой информации.


слайды 1-2 (Тема презентации "Формулы корней квадратных уравнений", пример)
После слайда с названием презентации следует слайд, на котором представлена общая формула квадратного уравнения, хорошо знакомая учащимся из предыдущих уроков изучения математики. Далее следует ряд сложных преобразований, конечной целью которых является выделения дискриминанта квадратного уравнения, знание которого является основополагающим и необходимо учащимся для дальнейшего применения при решении всевозможных квадратных уравнений.
Далее на слайде показаны различные преобразования формулы квадратного уравнения, в которые входит дискриминант. Сделано это для того, что бы учащийся лишний раз поработал с формулой дискриминанта и хорошо запомнил её, что бы в последующем без проблем применять на практике.


слайды 3-4 (примеры, определение степени)
На третьем слайде ученикам предлагается к рассмотрению теорема номер один, которая гласит, что в том случае, когда величина дискриминанта уравнения является отрицательной величиной, то решений рассматриваемое уравнение иметь не будет. Далее представлено доказательство первой теоремы. Для её доказательства применяются преобразования общего выражения уравнения, выполненные на первом слайде, что еще раз показывает, что вся информация в презентации следует в правильном и логичном порядке. В ходе доказательства теоремы учащиеся должны понять, что квадрат числа не может являться отрицательной величиной, и что если дискриминант уравнения, который приравнивается к выражению, стоящему под знаком квадрата, меньше нуля, то это противоречит законам и правилам математики.
Все теоремы, представленные в данной презентации, выделены другим цветом и курсивом, что приковывает внимание учеников и непроизвольно заставляет их запоминать выделенную информацию. Плюсом является также и то, что учащиеся могут сами прочитать теорему и переписать ее в тетради со слайда презентации, а не записывать под диктовку учителя.
После слайда, на котором учащимся объясняется первая теорема, следует пример, который хорошо показывает применение этой теоремы на практике. Решение уравнения расписано подробно, начиная от определения коэффициентов уравнения и заканчивая поиском дискриминанта.
Закрепив знания, полученные при изучении первой теоремы, вниманию учащихся предлагается вторая теорема, суть которой заключается в том, что когда величина дискриминанта уравнения является равной нулю, уравнение может иметь всего одно решение, которое определяется по специальной формуле. После формулировки теоремы следует ее доказательство, в ходе которого выводится формула, данная в самой теореме.
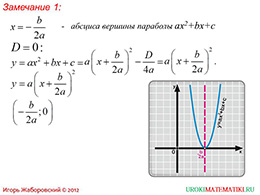

слайды 5-6 (примеры, определение возведения в степень)
На пятом слайде продолжается доказательство теоремы номер два. Для ее более полного усвоения учащимися, приведено также графическое изображение. Для его построения, используются формулы, для нахождения вершины параболы. Абсциссой вершины квадратного трехчлена является единственный корень квадратного уравнения, а ордината находится путем преобразования квадратного члена и подстановки в качестве дискриминанта нуля.
По полученным точкам строится парабола. Графическое изображение является очень удачным и понятным, так как, графики функций и координатные оси изображены разными цветами, а все необходимые точки подписаны. Исходя из данного графического изображения, и знаний, полученных на более ранних сроках изучения математики, учащиеся могут сделать вывод, что так как парабола качается координатной оси в одной точке, то у уравнения будет всего лишь одно решение.
Далее следует слайд, на котором приводится вариант уравнения, которое необходимо решить, используя знания, полученные при изучении второй теоремы. Как и при разборе предыдущего примера, сначала определены все необходимые для поиска дискриминанта коэффициенты, а затем найден сам дискриминант и выполнен поиск корня квадратного уравнения. После разбора примера следует примечание, которое призывает учеников к тому, что необходимо внимательно анализировать предложенное уравнение, для того чтобы не было необходимости выполнять лишнюю работу.
Так, примечание показывает пример, в котором квадратный трехчлен сворачивается по формуле полного квадрата, и поиск корня уравнения сводится к приравниванию выражения, стоящего под знаком квадрата к нулю, что значительно сокращает время, потраченное на решение уравнения.


слайды 7-8 (примеры)
На седьмом слайде вниманию учащихся представлена третья теорема, которая описывает наиболее сложный вариант, а именно вариант, при котором величина дискриминанта представляет собой положительную величину. Согласно изученным теоремам, решениями уравнения будут являться два числа, величины которых определяются по особым формулам, которые также представлены на слайде. Как и в предыдущих случаях, после формулировки теоремы следует ее подробное доказательство.
Доказательство является более сложным, чем доказательства предыдущих двух теорем и требует особого внимания как учащихся так учителя. Для доказательства третьей теоремы вводится дополнительная переменная, на которую заменяется выражение, стоящее под знаком квадрата, полученное в результате простейших преобразований квадратного трехчлена.
Вводится новая переменная величина для облегчения объяснения теоремы на самом первом этапе. Основывается доказательство в первую очередь на том, что как отрицательное, так и положительное число, возведенное в квадрат, дает положительную величину. Затем, снова перейдя к первоначальному выражению, которое было заменено на новую переменную величину, и выполнив несколько простейших математических операций выводятся формулы, необходимые для решения квадратного уравнения в том случае, если его дискриминант больше нуля.
Доказательство теоремы, как всегда сопровождается конкретным примером, представленным на восьмом слайде. Как и в предыдущих случаях определяются необходимые коэффициенты, определяется величина дискриминанта, и, исходя из знания новых формул для случая, когда величина дискриминанта является положительной величиной, находятся два решения. Для закрепления знаний и лучшего запоминания нового материала, каждое новое выражение сначала прописан в обобщенном виде, а лишь затем в него подставлены необходимые числа.


слайды 9-10 (пример, калькулятор)
Следующий слайд представляет собой обобщенную информацию предыдущих слайдов. На нем кратко и понятно описывается алгоритм решения квадратного уравнения для каждой из возможных ситуаций: когда дискриминант меньше нуля, когда он равен нулю, и когда дискриминант уравнения больше нуля. Данный слайд еще раз показывает учащимся, что прежде чем приступить к решению квадратного уравнения, необходимо посчитать его дискриминант, используя уже изученную формулу и коэффициенты квадратного трехчлена, которые в нее подставляются.


слайды 11-12 (примеры)
На десятом и одиннадцатом слайде вниманию учащихся представлены примеры решения различных квадратных уравнений. Материал презентации построен так, чтобы учащиеся как можно лучше усвоили новый материал и научились применять его на практике, а большое количество разнообразных примеров сделает учебный процесс наиболее оптимальным и правильным. На слайдах представлено подробное решение трех квадратных уравнений, условия которых даны в самом начале десятого слайда. Это сделано для того, что бы учащиеся могли переписать условия уравнений себе в тетрадь и попробовали решить их самостоятельно, опираясь на полученные раннее знания теорем и формул.
А подробно разобранные примеры решения предназначены для того, что бы учащиеся могли проверить правильность своего решения, и в случае необходимости исправить ошибку, возникшую на том или ином этапе решения уравнения. Три примера подобраны так, что бы при их решении могли быть использованы все три изученные теоремы. Уравнения расположены так, чтобы теоремы, которые необходимо применить для их решения шли не по порядку изучения, а в разброс, что заставляет ученика аккуратно и более внимательно подойти к поиску решения уравнения.
Первое уравнение рассматривает самый сложный случай, когда дискриминант больше нуля, второе уравнение имеет дискриминант равный нулю, то есть для поиска его решения учащимся необходимо применить всего одну формулу, а третье уравнение рассматривает самый простой случай, когда дискриминант равен нулю и уравнение не имеет корней.
Двенадцатый слайд еще раз обобщает информацию и знания, которые учащиеся получили, изучив предыдущие слайды. На данном слайде формулы для решения квадратных уравнений представлены в общем виде. На прошлых слайдах учащиеся получили информацию о том, как находить дискриминант, а затем, уже зная его величину, доводить решение до конца. Выражения, представленные на двенадцатом слайде, позволяют найти ответ в одно действие, сразу подставив все необходимые величины в то или иное выражение.


слайды 13-14 (примеры)
После того, как учащиеся овладели навыками поиска решений простейших уравнений с различной величиной дискриминанта и закрепили все полученные знания на практике, их вниманию предлагаются более сложные примеры уравнений. Так, в примере пятом разобраны примеры решения двух квадратных уравнений, коэффициенты которых являются дробными числами. Решение первого примера сводится к тому, что дробное уравнение преобразовывается к виду уравнения, в котором коэффициенты являются целыми числами.
Для этого дробные коэффициенты уравнения приводятся к общему знаменателю, который выносится за скобки, а правая часть уравнения умножается на число, равное числу, вынесенному за скобки, что не приводит к изменениям самого уравнения, но позволяют избавиться от дробей и приводит уравнение к удобному виду. Далее решение уравнения сводится к поиску дискриминанта и в зависимости от его величины использованию необходимых для поиска решения формул.
Второе уравнение, разобранное в пятом примере, также имеет в своем составе дробные числа, с которыми достаточно трудно проводить математические операции. Решение данного уравнения основывается на знаниях, полученных учащимися на более ранних сроках изучения математики. Для того, что бы привести данное уравнение к удобной форме, необходимо каждый из его членов умножить на одну и ту же величину, в результате чего смысл уравнение не изменяется, но оно приобретает удобный для дальнейшей работы вид. Дальнейшее решение уравнения сводится к использованию уже полученных учащимися знаниях.


слайды 15-16 (пример, калькулятор)
На пятнадцатом слайде представлен еще один пример решения квадратного уравнения. В примере шестом описывается план решения уравнения, имеющего иррациональный коэффициент, то есть один из коэффициентов стоит под знаком корня. Для решения данного уравнения необходимо применять знания, с помощью которых можно разложить на составные множители числа, стоящие под знаком корня. Данные знания необходимо применять для того, что бы привести выражения, являющиеся корнями уравнения к менее громоздкому и более красивому виду.
На последних двух слайдах представлены наиболее сложные примеры, а именно примеры решения квадратных уравнений с параметром. Если в уравнении некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами, то они называются параметрами, а уравнение параметрическим. Именно параметрические уравнения вызывают наибольшие затруднения при изучении в школе, и требуют особого рассмотрения и внимания.
В седьмом примере рассмотрен достаточно несложный пример параметрического уравнения, для его решения учащимся предлагается пользоваться стандартной схемой решения уравнения, заключающейся в поиске дискриминанта. Однако поскольку возможности сравнить дискриминант с нулем при решении параметрического уравнения не имеется, то в любом случае уравнение будет иметь два корня.
В качестве привычных коэффициентов, применяемых при решении квадратного уравнения, учащимся необходимо использовать выражения с параметром, стоящие перед переменной величиной. Несмотря на более длинную запись и наличие двух переменных величин смысл решения уравнения не изменяется, единственное отличие заключается в том, что корнями уравнения будет являться не конкретное число, а то или иное выражение с параметром.

слайд 17 (пример)
Восьмой пример является более сложным. Для решения данного уравнения учащимся предлагается в ходе решения принимать параметр равным тому или иному числу, от значения которого могут зависеть величины корней уравнения. Значения параметра следует выбирать так, что бы для начала один из коэффициентов, в состав которого входит параметр обращался в ноль, а затем, исключать это число из области значение параметра, для того, чтобы коэффициент не был равен нулю. Поиск корней уравнения следует осуществлять для каждого конкретного случая по отдельности, используя знания и навыки, полученные при изучении информации, представленной в данной презентации.
Данная презентация на тему «Формулы корней квадратных уравнений Часть 1» существенно улучшит уровень подачи материала на уроке математики в средней школе. Учебный материал, которые рассмотрен в данной презентации, может быть использован для изучения не только в школе под руководством учителя, но так же может являться прекрасным учебным пособием для изучения учащимися самостоятельно, или при помощи родителей. Материал изложен в легкой и доступной форме и прекрасно подходит для учащихся с любым уровнем первичной подготовки.
Просматривать данную презентацию можно не только с помощью компьютера, но и с помощью специализированного оборудования, а слайды имеют хорошо продуманную цветовую гамму и крупный шрифт, что позволяет хорошо видеть представленную информацию учащимся во всем классе, не зависимо от занимаемого ими места. Удобство при необходимости вернутся к тому или иному слайду за считанные секунды является огромным плюсом использования интерактивного материала, чего нельзя добиться при использовании обычной доски и мела.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 7401 |
| Номер материала | 299 |