
Презентация "Площадь трапеции"

Краткое описание документа:
На предыдущих уроках школьники ознакомились с нахождением площадей некоторых геометрических фигур, таких как квадрат, прямоугольник, треугольник и параллелограмм. Как можно было заметить, эти темы были взаимосвязаны между собой. Например, для нахождения площади параллелограмма, мы «преобразили» его в прямоугольник, с площадью которого уже были знакомы. А, при нахождении формулы площади треугольника, использовались предыдущие знания, ведь треугольник рассматривался как половина параллелограмма.
Тема данной презентации: «Площадь трапеции». Для начала стоит вспомнить, что же такое трапеция, и чем она отличается от других геометрических фигур? Школьники уже знаю, что данная геометрическая фигура обладает двумя параллельными основаниями. Прежде, чем приступить к рассматриванию формулы трапеции, стоит также вспомнить, как провести высоту трапеции к одной их оснований.

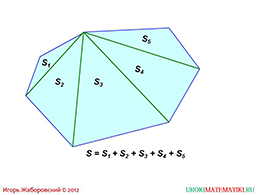
слайды 1-2 (Тема презентации "Площадь трапеции", пример)
Первый слайд презентации «Площадь трапеции» несет важную информацию. Желательно, чтобы учитель, репетитор или родитель озвучили объяснение, ведь страница содержит лишь иллюстрацию. Если ребенок достаточно сообразительный, то он сможет справиться и самостоятельно.
Итак, на чертеже видим некоторую геометрическую фигуру, а именно, многоугольник. Также, видим, что он разбит на пять треугольников путем соединения некоторой вершины со всеми остальными. Для того чтобы найти площадь данной фигуры, необходимо просуммировать площади всех треугольников. Это действительно так, ведь площадь параллелограмма можно представить в виде суммы двух площадей треугольников, из которых он состоит.
На последующем слайде дается определение высоты трапеции. Высота, как и в любой другой фигуре, является перпендикуляром, опущена на нижнее основание. Автор предлагает обозначить точку пересечения высоты латинской буквой H. Это достаточно распространенное общепринятое обозначение.
Для нахождения формулы площади трапеции необходимо выполнить некоторые дополнительные построения. А именно, необходимо провести высоту трапеции от правой вершины нижнего основания. Желательно, чтобы школьник перечертил фигуру с обозначениями, и попробовал самостоятельно провести высоту. В этом нет ничего сложного, а плюс заключается в том, что он запомнит идею нахождения площади трапеции.
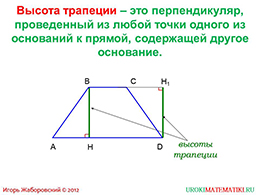

слайды 3-4 (определение высоты трапеции, теорема)
Следующий слайд говорит о том, что площадь трапеции можно выразить через произведение суммы оснований трапеции на высоту, деленную на два. В этой формуле нет ничего магического. Она имеет простое доказательство истинности.
Для этого необходимо вернуться к предыдущему рисунку, и внимательно на него посмотреть. На данном рисунке, мы получили прямоугольник. Проведем диагональ этой фигуры. Он будет разделять трапецию на два треугольника, а прямоугольник – на два равных треугольника, исходя их свойства диагонали прямоугольника.
Зная площадь прямоугольника, можно легко найти площадь одного из треугольников, которая входит и в ее состав и в состав трапеции. Таким образом, остается найти площадь второго треугольника, который входит в изначально рассматриваемую фигуру. Площадь треугольника BCD найти несложно, ведь мы знаем ее высоту.
Итак, площадь трапеции равна сумме найденных площадей треугольников. При математической записи полученной формулы и ее упрощении получим формулу для нахождения площади трапеций.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 4574 |
| Номер материала | 333 |