
Урок "Площадь треугольника"

Краткое описание документа:
Видеоурок по геометрии для 8-го класса поможет учащимся изучить тему о нахождении площади треугольника. В теме рассматривается, какой существует способ вычисления площади треугольника, приводятся два следствия, теорема об отношении площадей треугольников.
Вначале урока обозначим некоторые положения для упрощения рассмотрения темы. Рассмотрим для примера треугольник ABC. Часто для удобства одну из сторон в треугольнике принимают за основание. Тогда рассматриваемой высотой будет высота, которая проведена к основанию.
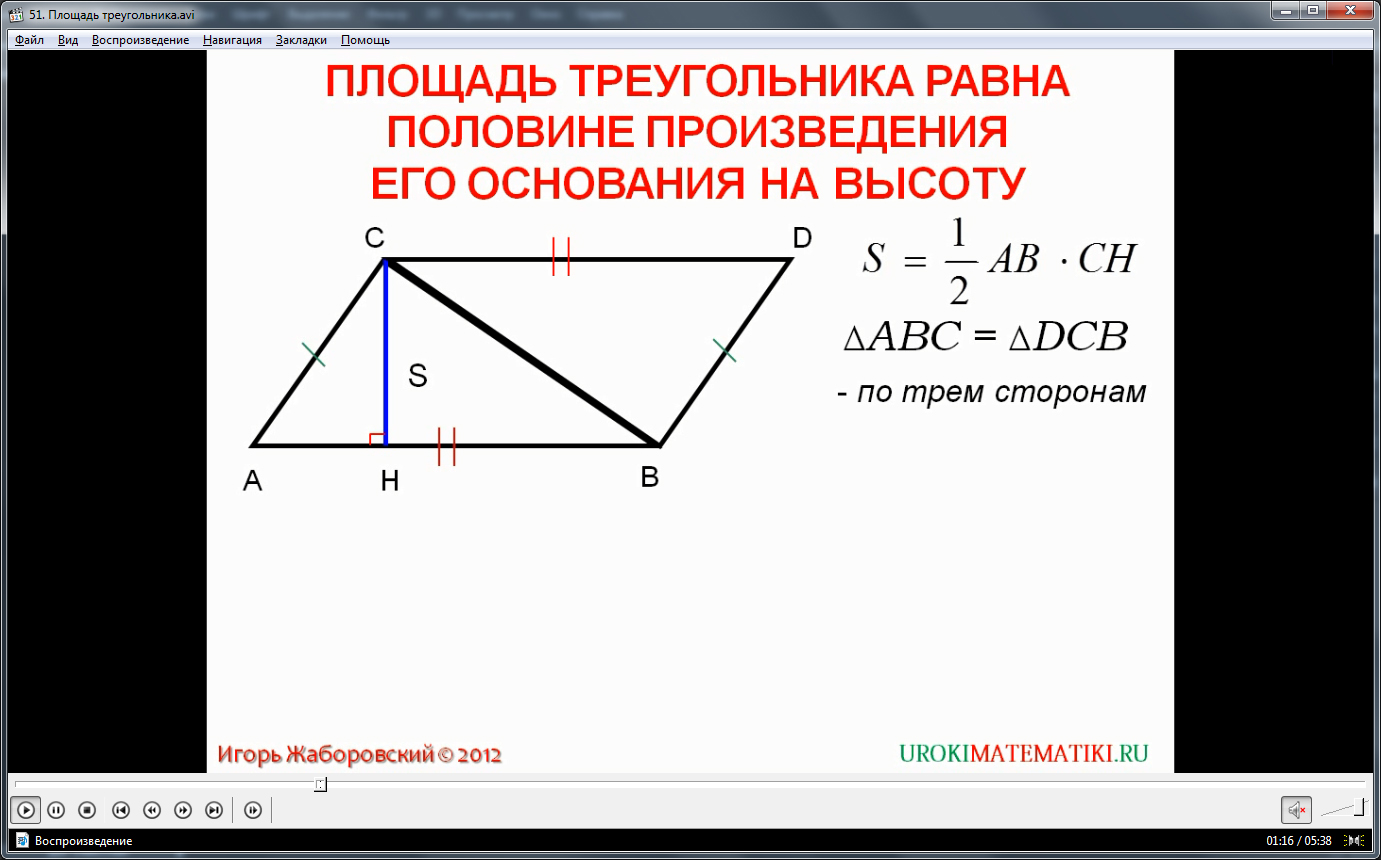
Разберем теорему: площадь треугольника можно вычислить как произведение его основания на высоту, деленное пополам. Утверждение требует доказательства. Допустим, дан треугольник ACB, где его площадь выражается значением S. Будем считать, что сторона AB – это основание треугольника. Проведем перпендикуляр CH. Нужно доказать, что S = 0,5 x AB x CH.

Воспользуемся следующим методом: на основе треугольника ACB начертим параллелограмм ABCD как показано на рисунке. Рассмотрим треугольники ACB и CBD. CB – это их общая сторона, сторона BA равна DC, сторона CA равна DB, таккак это лежащие напротив друг друга стороны параллелограмма. Треугольники ACB и CBD равны, так как выполняется равенство трех сторон. Из равенства треугольников следует, что равны и их площади. Следовательно, площадь треугольника ACB равна площади параллелограмма ABCD, деленной пополам. Мы знаем, что площадь параллелограмма можно вычислить путем умножения основания на высоту: SABCD = AB x CH. Значит, площадь треугольника находится как S = 0,5 x AB x CH, что и необходимо было доказать.
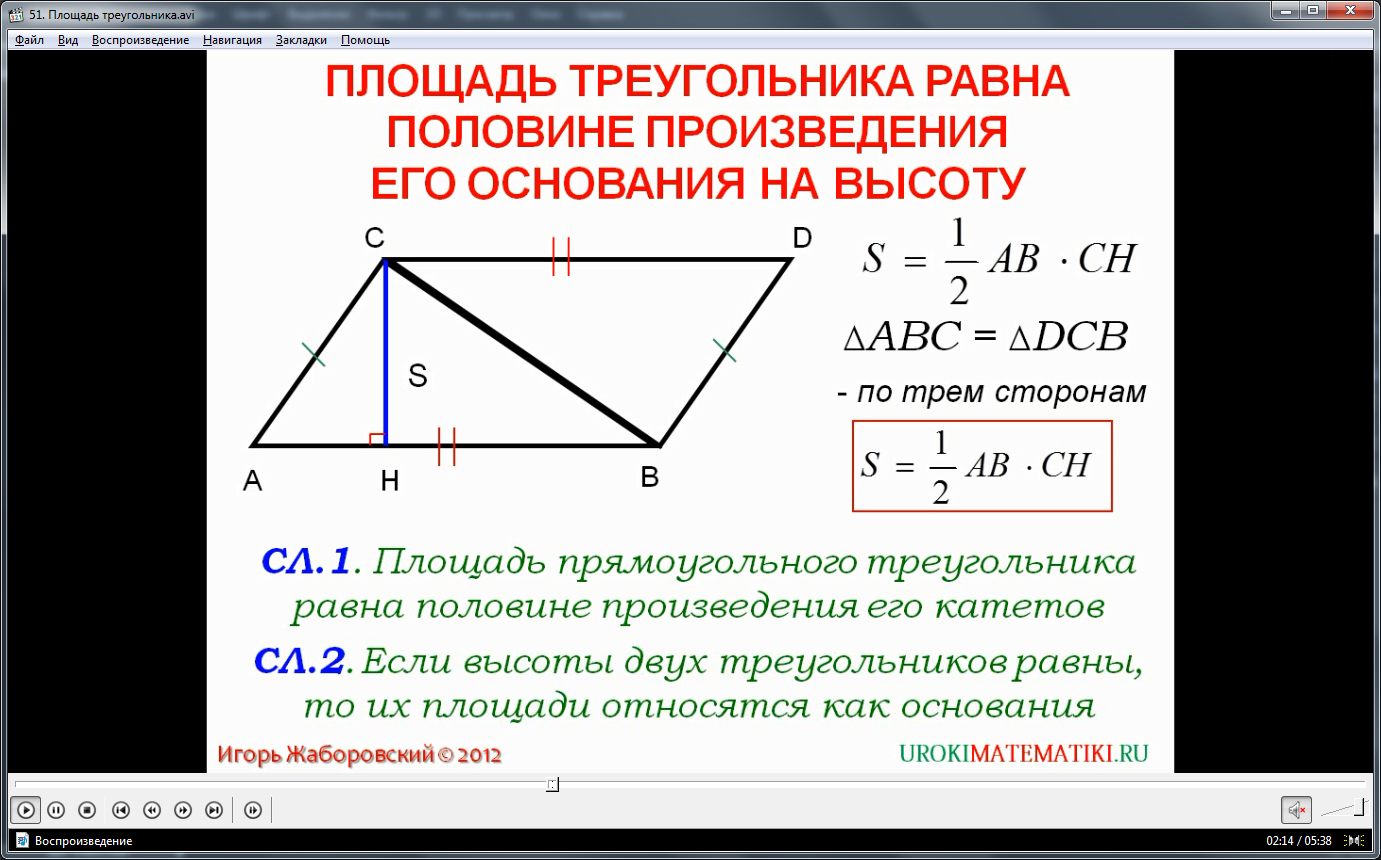
Из теоремы следует несколько утверждений.
Первое следствие. Площадь прямоугольного треугольника находится как произведение катетов, деленное на 2.
Второе следствие. Если в двух треугольниках высоты равные, то отношение площадей треугольников равно отношению их оснований.
Второе следствие можно применить при доказательстве теоремы об отношении площадей треугольников, в случае, когда у них один из углов равный.
Эта теорема говорит о том, что, если в двух треугольниках выполняется равенство одного из углов, то отношение площадей этих треугольников будет равно значению отношения произведения сторон, которые заключают равные углы.
Разберем доказательство. Пусть даны два треугольника ABC и A1B1C1, площади которых равны соответственно S и S1. Известно, что угол А равен углу А1. Докажем, что верно выражение S / S1 = (AB x AC) / A1B1 x A1C1, т.е. площади этих треугольников относятся друг к другу как произведения сторон, которые заключают равные углы.
Далее совместим два треугольника таким образом, чтобы вершина A совпала с вершиной A1, а стороны A1B1 и A1C1 совпали с лучами AB и AC.Треугольники ABC и AB1C (выделен цветом на рисунке) имеют общую высоту CH. Запишем площади этих треугольников. Площадь треугольника ABC равна 0,5 x AB x CH. Площадь треугольника AB1C равна 0,5 x AB1 x CH. Тогда площади относятся друг к другу как (0,5 x AB x CH) / (0,5 x AB1 x CH) или AB / AB1. По аналогии, треугольники AB1C и AB1C1 также имеют общую высоту B1H1 (отмечена на рисунке). Площадь треугольника AB1C1равна 0,5 x A1С1 x BH1, а площадь треугольника AB1C можно записать по-другому как 0,5 x AC x BH1.

Тогда площади треугольников AB1C и AB1C1 относятся друг к другу как (0,5 x AC x BH1) / (0,5 x A1С1 x BH1) или AС / AС1. Перемножив полученные равенства, найдем, что площади треугольников ABC и AB1C1 относятся друг к другу как (AB x AC) / (AB1 x AC1). Т.е. S / S1 = (AB x AC) / A1B1 x A1C1. Мы доказали теорему.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6017 |
| Номер материала | 589 |