
Презентация "Площадь треугольника"

Краткое описание документа:
Следующая геометрическая фигура, которую предстоит рассмотреть ученикам в ходе изучения геометрии – это треугольник. О том, что такое треугольник, ученики уже давно знают. Это геометрическая фигура, которая имеет три стороны и три угла. Известны такие типы треугольников, как остроугольные и тупоугольные, также рассматривался в отельном случае прямоугольный треугольник. Помимо классификации, согласно углу, учеников знакомили также с равнобедренными и равносторонними треугольниками.
Урок «Площадь треугольника» объяснит школьникам, как следует находить площади любого треугольника, зная некоторые данные о ней. Существует универсальная формула, которая подойдет для нахождения меры абсолютно любого из вышеперечисленных вида треугольников. Эта формула содержит в себе высоту. Прежде, чем приступить к изучению, стоит предложить учащимся начертить некоторый произвольный треугольник.

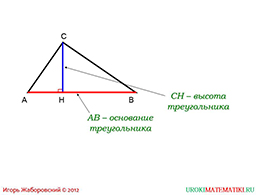
слайды 1-2 (Тема презентации "Площадь треугольника", пример)
Далее, стоит провести высоту к основанию треугольника ABC – AB. Высоту обозначить следует привычным образом, то есть точку пересечение высоты с основанием – H. Таким образом, CH –высота треугольника.
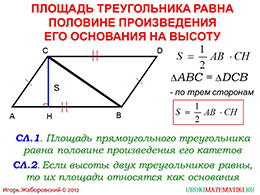
На следующем слайде приводится формула, по которой можно найти площадь произвольного треугольника. Она будет равняться половине произведению основания, в данном случае AB, на высоту (CH). Возникает вопрос о том, откуда появилась данная формула? Если «дополнить» данный треугольник, проведя отрезок, равный основанию треугольника и параллельный ему от вершины треугольника С, и аналогичным образом поступить со стороной AC, то получим еще один треугольник, симметричный нашему относительно стороны CD.
По признаку равенству треугольников, а именно по трем сторонам, данные треугольники равны. Это видно и по рисунку. Таким образом, мы получили некоторый параллелограмм. Обозначим его ACBD. Нахождение площади параллелограмма рассматривалось на прошлом уроке. К моменту изучение этой темы, школьники должны уметь пользоваться данной формулой.
Итак, что же нам дают дополнительные построения? Зная площадь параллелограмма, можем выразить площади равных треугольников. Параллелограмм разбит на две равные части, следовательно, площадь каждого из треугольников будет равна половине площади параллелограмма. Если записать эту формулу, то получим половину произведения высоты параллелограмма на основание. Высота треугольника и параллелограмма является общей, как и основание.
Ниже, на этом же слайде, рассматриваются площадь прямоугольного треугольника. Так как в такой фигуре высота и сторона, а именно, один из катетов, совпадают, то можно сформулировать площадь, как половина произведения катетов.
слайды 3-4 (вычисление площади треугольника)
Также рассматривается случай двух треугольников с одинаковыми высотами. Можно выяснить, что отличие в их площадях будет зависеть от основания, то есть чем больше основание, тем больше будет площадь того или иного треугольника.
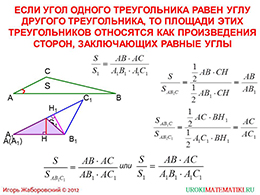
На следующем слайде рассматривается случай при вычислении площадей некоторых двух треугольников, которые имеют одинаковый угол. Можно выяснить, что площади будут относиться как произведения сторон, между которыми находится равный угол. Доказать это утверждение можно очень просто. Именно это и демонстрируется на слайде. Будет очень эффективным, если материал будет озвучен учителем или репетитором. Однако, если ребенок способный, он сможет разобраться в материале и самостоятельно. Ведь каждый этап рассматривается максимально подробно и понятно.
После изучения данного материала, школьники могут подумать над формулами нахождения различных видов треугольников, с которыми они уже ознакомились. Стоит использовать изученную на данном уроке формулу. Это поможет запомнить ее и научиться применять ее на практике.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6267 |
| Номер материала | 332 |