
Презентация "Практические приложения подобия треугольников"

Краткое описание документа:
Презентация «Практические приложения подобия треугольников» поможет учителям более понятно и доступно объяснить восьмиклассникам один из важных уроков из курса геометрии. Материал не такой уж и простой, как может показаться на первый взгляд. Необходимо уделить ей достаточно внимания, чтобы школьники хорошо усвоили эту тему. В дальнейшем, тригонометрические задачи будут появляться на практике в домашних заданиях и контрольных работах. Чтобы у учеников восьмого класса успеваемость была на высоком уровне, необходимо, чтобы они не пропускали ни один урок, ведь темы, как в геометрии, так и в алгебре являются взаимосвязанными.
Презентация имеет понятную структуру. На слайдах элементы высвечиваются последовательно. Текст не является сложным, он написан с учетом того, чтобы школьники могли максимально хорошо понять. Нет отвлекающих ярких цветов, узоров на фоне и прочее.

слайды 1-2 (Тема презентации "Практические приложения подобия треугольников", пример)
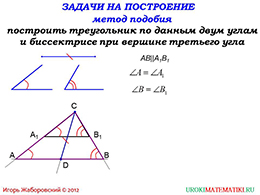
На первом слайде мультимедийного файла предлагается выполнить задачу на построение. Необходимо получить треугольник, имея при этом два известных угла и биссектрису при вершине третьего угла. Как же это необходимо выполнить?
Ниже высвечивается три элемента. Первый элемент – это отрезок, который в результате будет являться биссектрисой полученного треугольника. Следующие два элемента – это данные углы. Мы видим, что у них разная мера. Это говорит о том, что получим неравнобедренный треугольник. Остается построить требуемую фигуру.
В результате построения получили треугольник, у которого при основании имеются два заранее заданных угла. Однако если провести параллельно основанию отрезок, проходящий через нижнюю вершину биссектрисы, то получим искомую фигуру. К тому же, можно увидеть, что углы при основаниях у первого и у второго треугольника равны, а вершина у них одна. Это говорит об их равенстве.
слайды 3-4 (примеры)
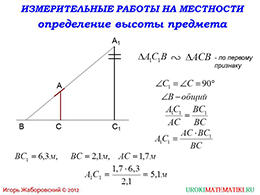
На следующем слайде имеем два подобных треугольника. При этом, если внимательно рассмотреть их, то можно выяснить, что они прямоугольные. На данном слайде будет говориться о нахождении высоты. Так как треугольники являются подобными по первому признаку, то отношение их высот, будет равен отношению их катетов, к которым опущены высоты. Из пропорции можно выразить искомую высоту.
Чтобы было понятнее, ниже приводится пример с численными значениями. Если восьмиклассники не смогут решить их самостоятельно, то можно продемонстрировать им решение из этого же слайда. Аналогичным же образом можно найти и другие стороны, использую знания о подобных треугольниках.
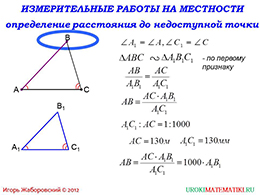
Перейдем далее. На этом слайде имеем два треугольника. Необходимо найти сторону AB, которая принадлежит первому треугольнику.
слайд 5 (пример)
Для начала необходимо исследовать фигуры. Как видно, они являются подобными. Ведь они имеют два равных угла, что говорит о том, что выполняется первый признак подобия треугольников.
Исходя из подобия треугольников, можно написать пропорциональное соотношение соответствующих сторон. Из получившегося равенства можно выразить искомую сторону. Для лучшего понимания дается пример с численными значениями. Основание маленького треугольника в тысячу раз меньше основания большого треугольника. Также известны длины этих оснований.
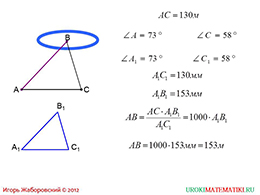
Численное решение приводится на следующем слайде. Здесь же даны меры углов. Выразим из равенства, которое получили на прошлом слайде искомую сторону. Далее, подставим имеющиеся данные. Таким образом, получим длину искомой стороны. Другими словами, получили расстояние до недопустимой точки.
Итак, благодаря данному мультимедийному файлу школьники ознакомятся с построением подобных треугольников, также научаться находить высоту некоторого треугольника, зная данные о сторонах подобного ему треугольника. Очень важно, чтобы ученики восьмого класса научились составлять пропорции и работать с ними, то есть выражать некоторые элементы из равенства.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 7941 |
| Номер материала | 344 |