
Презентация "Синус, косинус и тангенс острого угла прямоугольного треугольника"

Краткое описание документа:
Одной из важнейших и сложных тем, с которыми должны столкнуться восьмиклассники, это основы тригонометрии. Речь идет о понятиях синуса, косинуса, тангенса и котангенса. Начать изучение стоит с рассмотрения этих понятий на примере острого угла треугольника. Тригонометрия связано, непосредственно, с прямоугольными треугольниками.
Школьники должны очень хорошо понять данную тему, следовательно, учитель должен суметь максимально подробно объяснить каждый момент, продемонстрировать всевозможными слайдами. Данная презентация станет отличным помощником и для учителей и для учеников восьмого класса.

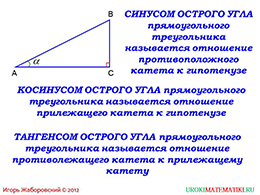
слайды 1-2 (Тема презентации "Синус, косинус и тангенс острого угла прямоугольного треугольника", пример)
Урок начинается с понятия синуса. Перед нами проиллюстрирован прямоугольный прямоугольник. Острый угол обозначен через «альфа», треугольник – ABC. Для того, чтобы найти синус угла альфа необходимо поделить противолежащий катет на гипотенузу. Для того чтобы найти косинус угла альфа необходимо поделить прилежащий катет к гипотенузе. Тангенс же является отношением синуса угла альфа на косинус. Если выполнить данное действие и преобразовать, то получим отношение катетов, а именно, противолежащего катета к прилежащему катету.
Чтобы не ограничиться теорией, на следующей странице урока приводится конкретные алгебраические записи синуса, косинуса и тангенса угла альфа. Как и любые понятия, которые изучаются в процессе алгебры и геометрии, необходимо изучить их обозначения. Их можно увидеть рядом с иллюстрацией прямоугольного треугольника, острый угол которого и рассматривается. Ниже записаны алгебраические формулы определений, которые проговаривались выше. Как видим, дается два варианта, с помощью которых можно выразить тангенс угла.
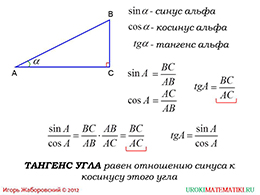
слайды 3-4 (примеры)
Рекомендуется, чтобы школьники делали записи в ходе обучения. Ведь просто просмотрев презентацию и прослушав объяснения, они не запомнят всю информацию. На первый взгляд, это покажется довольно сложным, ведь появляются новые определения, новые понятия и обозначения. Однако если усердно постараться, то не возникнет никаких недоразумений.
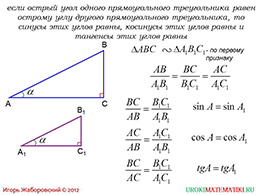
Перейдем на следующий слайд презентации «Синус, косинус и тангенс острого угла прямоугольного треугольника». Здесь используются знания, которые получили школьники на предыдущем уроке, а именно, подобие треугольников. Предположим, что имея два прямоугольных треугольника, острые углы у них будут равны.
Далее, приводится одна из важнейших формул, которая говорит о том, что сумма квадратов синуса некоторого угла и косинуса этого же угла равняется единице. Это является основным тригонометрическим тождеством. Из этого тождества в дальнейшем будут выведено множество различных формул, которые будут необходимы для различных тригонометрических преобразований.
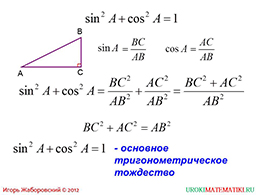
слайд 5 (пример)
Чтобы доказать верность основного тождества необходимо подставить имеющиеся формулы вместо синуса угла, косинуса угла, возвести их в квадрат и найти сумму. Данное выражение будет равняться единице, что доказывает истинность тождества.
В заключение урока стоит предложить школьникам решить некоторые задачи, связанные с нахождением косинуса, синуса и тангенса некоторых острых углов прямоугольных треугольников. Также, предложите им выполнить преобразования над простейшими тригонометрическими выражениями.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 11583 |
| Номер материала | 346 |