
Презентация "О подобии произвольных фигур"

Краткое описание документа:
Проведение уроков геометрии станет более поротым и увлекательным, если параллельно обычным традиционным объяснениям будут демонстрированы иллюстрации, рисунки, слайды и видеоуроки. Это упростит восприятие изучаемых объектов и геометрических фигур.
Благодаря презентации «О подобии произвольных фигур» учителя могут составить более понятный план-конспект для урока, правильно сконструированный и последовательный. В дальнейшем, школьники могут самостоятельно просмотреть документ и восстановить информацию, полученную на уроке. Ведь у большинства людей визуальная память развита лучше всего.


слайды 1-2 (Тема презентации "О подобии произвольных фигур", определение подобных фигур)
На предыдущих уроках ученики восьмого класса ознакомились с подобными треугольника, какие признаки подобия существуют, какими свойствами они обладают. Разумеется, и другие фигуры могут быть подобными. Будь то двумерные фигуры, будь то трехмерные или n-мерные. Объяснить данный урок без визуальной демонстрации будет тяжело и не очень эффективно, в особенности, если у ученика плохое пространственное мышлении и проблемы с геометрией.
На первом вступительном слайде можно ознакомиться с общим определением о подобии произвольных фигур. Фигуры условно обозначаются как F и F1. Данные фигуры можно назвать подобными, если при рассмотрении каждой точки, принадлежащей фигуре F, ей можно будет сопоставить точку, принадлежащей второй фигуре таким образом, чтобы выполнялось некоторое условие. Это условие продемонстрировано на слайде. Оно говорит о том, что соотношения расстояний между любых двух точек первой фигуры и между сопоставимыми точками во второй фигуре будет равняться определенной константе. Эта константа будет одинаковой для любых подобных соотношений. При этом, он будет называться коэффициентом подобия.
слайды 3-4 (примеры)
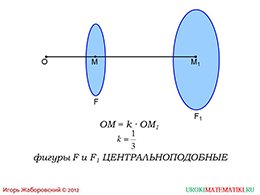
Далее, автор презентационного урока «О подобии произвольных фигур» предлагает перейти к рассмотрению центральноподобных фигур. На странице проиллюстрирован пример таких фигур. Пример приведен на основе эллипсов на двумерном пространстве.
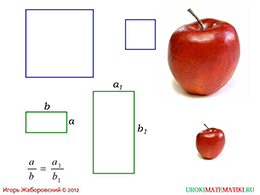
На завершающем этапе мы видим примеры некоторых подобных фигур. Например, два подобных квадрата, два подобных прямоугольника. На примере прямоугольника демонстрируется отношение сторон малой и большой фигуры.
Подобными могут быть и пространственные фигуры. В качестве примера даются подобные яблоки. Проверить это математически без специальных знаний будет тяжело, однако, это видно визуально.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 8502 |
| Номер материала | 345 |