
Урок "Практические приложения подобия треугольников"

Краткое описание документа:
Смысл каждой науки направлен на оптимизацию и упрощение жизни, на возможность практического применения. Геометрия, как одна из представительниц математически наук, также служит человечеству с практической точки зрения, к сожалению, мы не всегда умеем правильно использовать, полученные в школе, теоретические знания, считая их бесполезными. Представленная вашему вниманию презентация была специально разработана для того, чтобы показать значимость и необходимость изученного вами ранее материала относительно треугольников, его свойств, признаков подобия и прочего, в повседневной жизни.
Итак, для начала следует немного вернуться назад и повторить некоторые понятия. Что такое треугольник? Вы уже знаете, что под этой фигурой подразумевается элементарный многочлен, состоящий из трех точек, поочередно соединенных тремя отрезками.
Также дальнейшее раскрытие сегодняшней темы требует вспомнить и подобие треугольников. Их существует три. Во-первых, треугольники считаются подобными, если два из трех углов попарно равняются друг другу. Во-вторых, существует признак подобия, по которому треугольники равны, если две стороны одного треугольника пропорциональны двум сторонам другого, а углы между ними равны. В-третьих, подобие также определяет пропорциональность всех трех сторон.
На что же нам предлагает обратить внимание данная презентация? Во-первых, это задачи на построение. То есть по наличию части элементов необходимо построить геометрическую фигуру. Во-вторых, слайд-материалы предлагают рассмотреть пример на расчеты высоты объектов в том случае, когда измерить его каким-либо прямым способом не является реальным, например, высоту дерева, столба, многоэтажного дома, или же высоту пирамиды в Древнем Египте. В-третьих, определение расстояния от заданной точки положения до другой точки, расположенной, например, на другом берегу.
Во всех этих указанных случаях, геометрия имеет огромное значение в решении практических задач. Со своей же стороны, человеку достаточно применить немного смекалки.
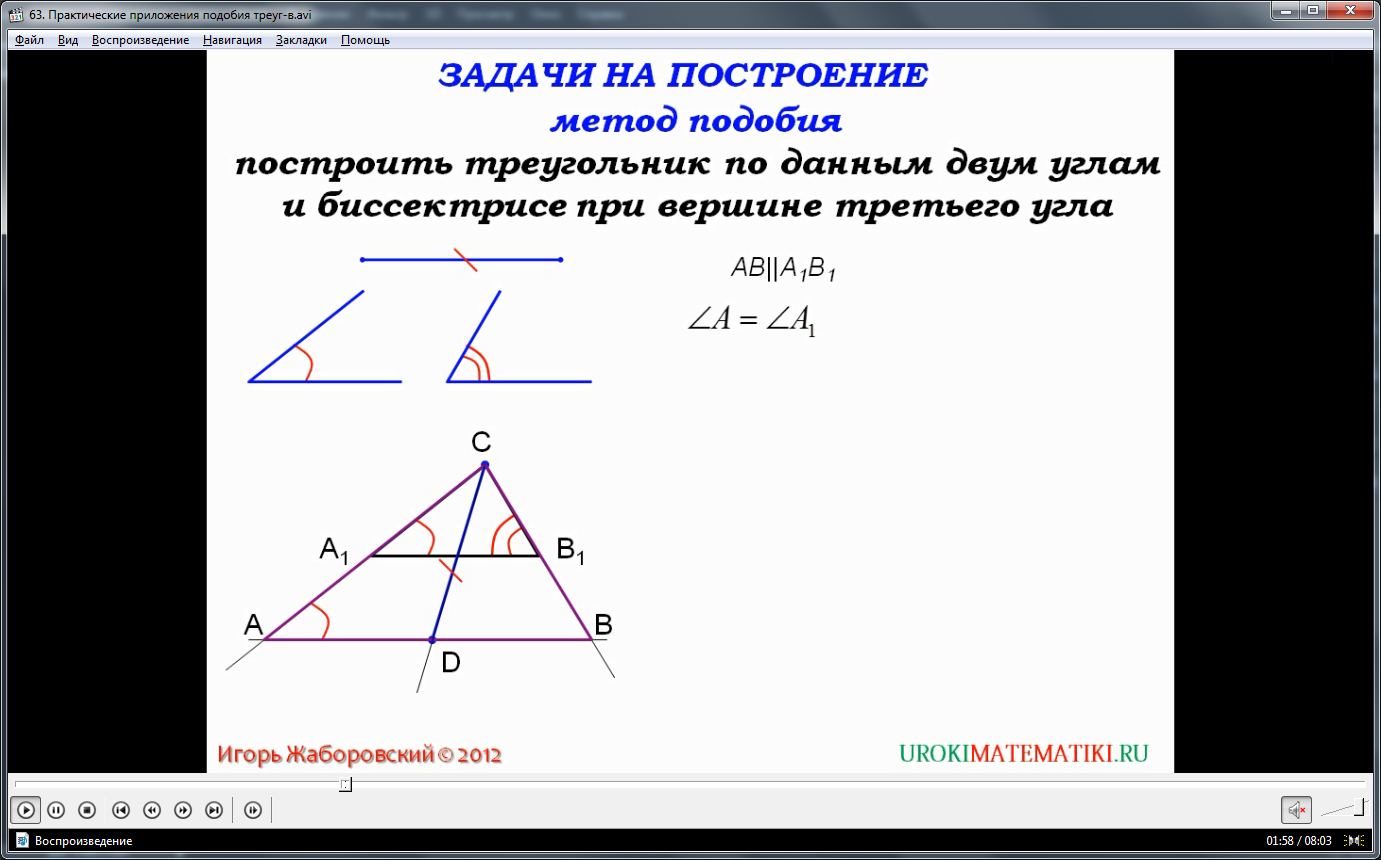
Итак, первое задание, которое нам предлагает решить наша презентация – это построение треугольника, исходя из трех известных нам величин, именно: величины двух углов, а также биссектрисы третьего их них. Графическое решение данного задания приведено на слайдах достаточно подробно, поэтому следует большее внимание уделить рассмотрению именно на них. Со своей же стороны кратко укажем ход решения. Имея только заданные величины, построение будет иметь следующий алгоритм. Сначала строим некий небольшой треугольник с заданными углами. Проводим биссектрису из образованного угла. Если она пересеклась с противоположной стороной треугольника, но не закончилась на ней, то через точку окончания биссектрисы параллельно прямой, противоположной третьему углу стороны треугольника, проводим прямую, другие стороны продлеваем до их пересечения. Таким образом, исходя из ограниченного количества данных, мы смогли построить искомый объект.
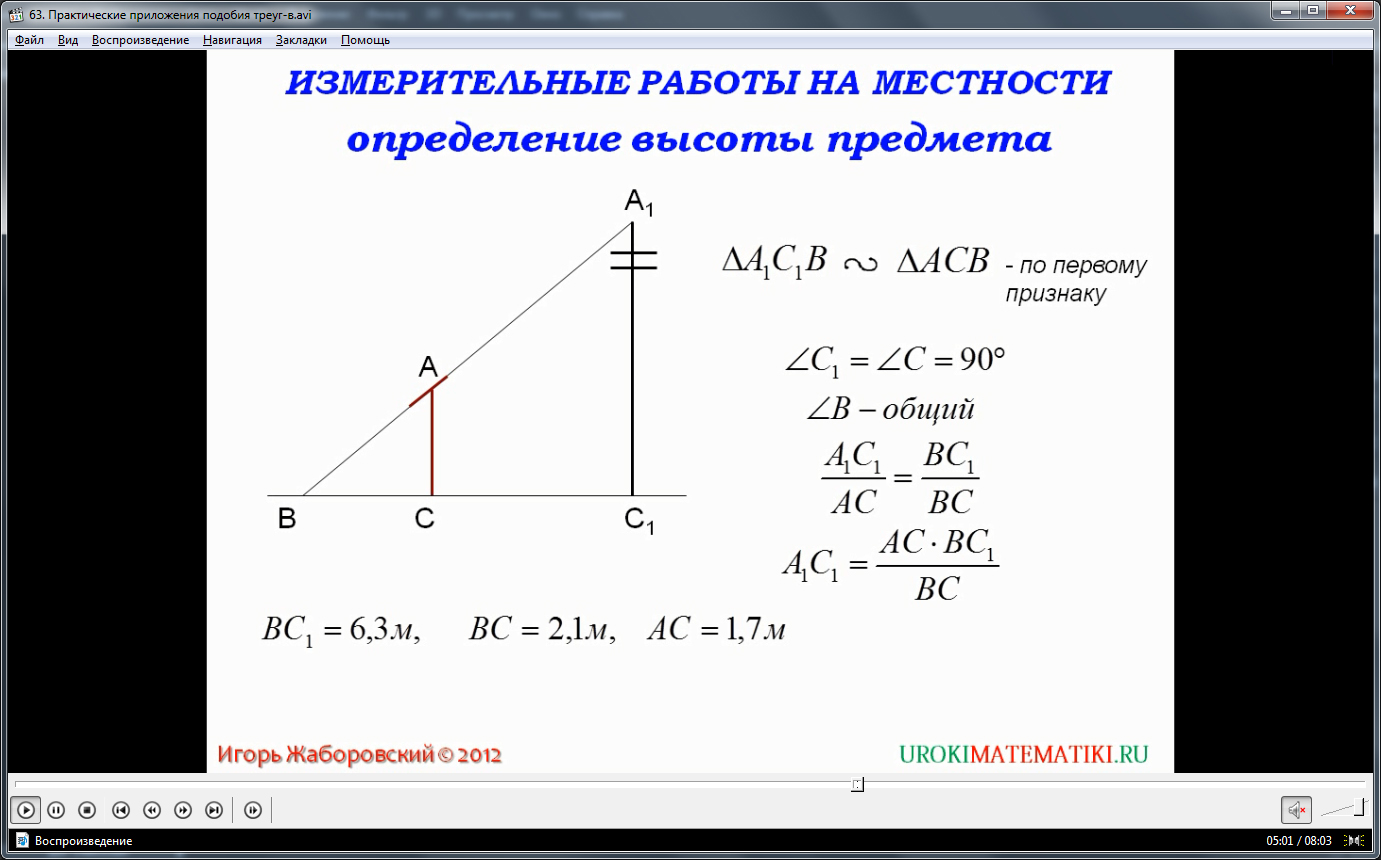
Также в презентации представлено еще две практически ориентированные задачи. И с ними вы познакомитесь, изучив более детально предложенный материал. Оба примера также основаны на принципах подобия треугольников. Суть их заключается в том, что имея значение коэффициента подобия, вы сможете, измерив небольшие, доступные к инструментальному определению, величины, узнать те, которые не поддаются такому способу определения. Как не всегда есть возможность залезть на дерево с линейкой, так и нет в этом вообще никакой необходимости, ведь верные данные можно получить, прибегнув к несложным расчетам.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 5993 |
| Номер материала | 601 |