
Презентация "Описанная окружность"

Краткое описание документа:
Данная презентация является хорошим электронным обучающим пособием, которое поможет вспомнить изученный материал абитуриентам, изучить уроки и решить домашнее задание школьникам восьмого класса. Также, с помощью этой презентации учителя могут сделать более структурированный план-конспект, который станет отличным помощником при проведении урока.

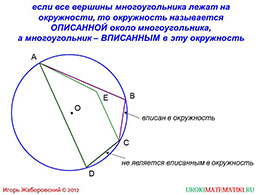
слайды 1-2 (Тема презентации "Описанная окружность", определение описанной окружности)
На прошлом уроке были рассмотрены и изучены вписанные окружности. Пора перейти к изучению описанных окружностей. С помощью презентации «Описанные окружности» школьники восьмого класса смогут ознакомиться с этим понятием и увидеть проиллюстрированные примеры. Исходя из полученного материала, будут объяснены высказывания, выводы и доказательства. Перейдем к рассмотрению первого слайда.
Здесь будет приведено определение описанной окружности. В таком случае, многоугольник, около которого описана окружность будет называться вписанной. В каком же случае окружность будет называться описанной? Если все вершины некоторого многоугольника лежат на окружности. Запомнить это будет просто, ведь перед глазами ученика будет проиллюстрирован пример. Зеленым цветом обведен многоугольник, около которого окружность не является описанной, ведь одна из вершин не лит на окружности.
слайды 3-4 (примеры, теорема)
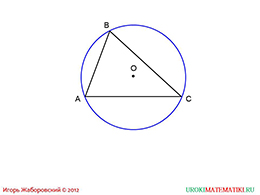
Далее, автор предлагает школьникам посмотреть на иллюстрацию, на которой изображен треугольник, который вписан в окружность. Чтобы убедиться в этом, нужно проверит все три вершины. Как видим, все они лежат на окружности. Перейдем далее.
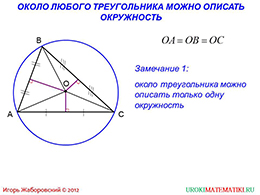
Здесь говорится о том, что около любого произвольного треугольника можно описать окружность, причем, только одну. Это напоминает случай со вписанной окружностью. Для доказательства используется материал, о котором говорилось в предыдущих уроках. Речь идет о точке пересечения высот. Доказывается, что отрезки, соединяющие центр окружности с вершинами треугольника являются радиусами данной окружности. Это и доказывает верность исходного выражения.
слайд 5 (замечание)
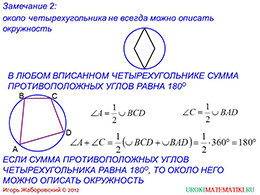
На следующем слайде рассматривается иной многоугольник, а именно, четырехугольник. Как и в случае вписанных окружностей, около не всех прямоугольников можно провести описанную окружность. Ниже приводится информация о том, каким образом можно выразить сумму противоположных углов четырехугольника, используя свойства описанных окружностей. Эта сумма будет равняться 180 градусам. Приводится доказательство. Стоит понимать, что обратное высказывание является также верным.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5306 |
| Номер материала | 355 |