
Презентация «Целое уравнение и его корни»

Краткое описание документа:
Данная презентация посвящения изучению целых уравнений и нахождению их корней. Она поможет учителю вести качественный урок, который можно донести до каждого ученика. Благодаря использованию данного электронного ресурса во время урока можно заинтересовать как можно больше учащихся. Таким образом, они смогут как можно больше понять и лучше запоминать, ведь помимо объяснений учителя у них будет работать зрительная память.


Также, с помощью презентации можно донести весь запланированный материал, не подглядывая в конспекты, что отвлекает учеников и вызывает сомнения к знаниям учителя. С этим часто сталкиваются молодые начинающие учителя.
Презентация содержит 10 слайдов, включая приветственную страницу, на которой содержится тема урока.
Итак, что же такое целое уравнения, и чем оно отличается от остальных? Это демонстрируется на второй странице презентации. Здесь же дается общая форма записи целого уравнения – p(x). Приводится 6 примеров уравнений, которые содержат целые выражения и с левых, и с правых сторон.


Далее рассматривается понятие «степень уравнения». Приводятся примеры. Можно заметить, что в определениях основные понятия выделяются красным цветом, что помогает сконцентрировать как можно больше внимание учеников.
Далее приводится на слайде уравнение первой степени в общем виде. С этой записью еще придется столкнуться неоднократно. Переменная, традиционно, обозначается через x, коэффициент – a, а свободный член – b. Отмечается, что коэффициент перед переменной не может равняться нулю, иначе уравнение потеряет смысл.
Ниже приводится ответ уравнения – то есть ее корень. Для того, чтобы решить ее необходимо разделить свободный член на коэффициент при неизвестном и поставить знак минус перед дробью. Также приводится утверждение о том, что уравнения первой степени всегда имеют один корень, какими бы они ни были. Учитель может подробно прокомментировать каждое утверждение и привести больше примеров для самостоятельного рассмотрения.


Следующий слайд посвящен уравнению второй степени. Приводится стандартный вид записи подобных уравнений, где переменная – x, коэффициент при неизвестной второй степени – a, при первой – b, а свободный член – c. При этом, первый коэффициент не может равняться нулю, как и в предыдущем случае, это не будет иметь смысла.
Для решения подобного уравнения, необходимо вспомнить формулу дискриминанта. Если школьники пропустили эту тему, то лучше вспомнить. На слайде приводится рассмотрение трех случаев дискриминанта, при которых он больше нуля, меньше, либо равняется. В зависимости от этого корни уравнения будут иметь разные значения. Можно заметить, что уравнения второй степени могут иметь один корень, два корня, либо ни одного.
Шестой слайд демонстрирует информацию об уравнениях третьей и четвертой степеней. Как и на предыдущих слайдах, первым делом дается общее представление подобного рода уравнений. Нетрудно догадаться, что уравнение третьей степени не может иметь более 3х корней, а четвертой степени – не более 4х.


На седьмом слайде дается подсказка о том, что некоторые уравнения 3й или 4й степени лучше всего решить с помощью предварительного разложения на множители. Приводится пример, чтобы продемонстрировать верность данного утверждения.
При разложении на множители уравнения третьей степени, зная свойство произведения, равного нулю, можно приравнять каждый множитель нулю. Ведь произведение будет равняться нулю только в том случае, когда хотя бы один из множителей будет равняться нулю.
Следующий слайд представляет собой еще один способ решения уравнений, которые имеют степень больше двух. Речь идет о введении новой переменной, что может упростить в разы задачу. Приводится пример решения уравнения и показывается, как стоит делать, и как не нужно.
Девятый слайд посвящен биквадратным уравнениям. Здесь демонстрируется общий вид подобного уравнения, а на последующем слайде приводится решение на некотором примере.

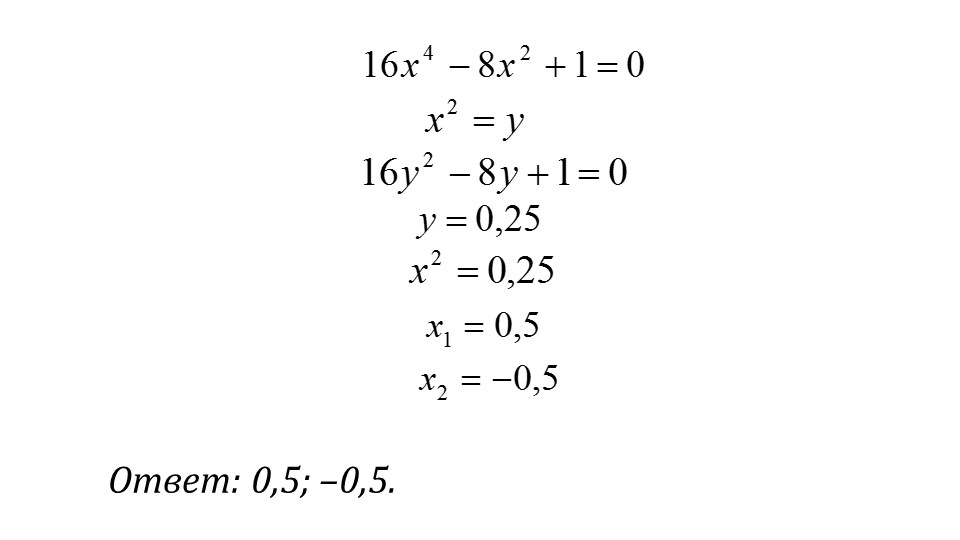
Если хорошо понять, что такое биквадратное уравнение, и решить некоторые практические примеры, можно очень быстро распознать их среди других и справиться без трудностей.
Данная презентация станет полезной не только во время урока в школе. С помощью нее можно вспомнить изученный материал дома, либо изучать с нуля при пропусках в школе.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 7995 |
| Номер материала | 627 |