
Научная работа "В помощь на ЕГЭ (об одном способе решения задач на концентрацию, смеси и сплавы)"
МКОУ СОШ № 2 с.Бешпагир
В помощь на ЕГЭ
(об одном способе решения задач
на концентрацию, смеси и сплавы)
Выполнила: Корбезашвили Екатерина
ученица 10 класса
МКОУ СОШ № 2 с.Бешпагир
Научный руководитель:
Ефименко С.И. учитель математики
Бешпагир, 2018
Содержание:
1. Введение
2. Задачи на смеси и сплавы
2.1 Задача из « Занимательной алгебры» Я.И. Перельмана
2.2 Старинный способ решения задач
2.3 Квадрат Пирсона
3 Решение задач на смеси и сплавы
4. Заключение
5. Использованная литература
Введение.
Первый же тренировочный вариант экзаменационных работ для проведения государственной итоговой аттестации в новой форме для 9 класса содержит задачу: «Имеются два сплава с разным содержанием золота. В первом сплаве содержится 30% , а во втором 55% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?». Эта задача была предложена ученикам 9 «Б» класса, в котором я учусь. Результаты показали, что не все смогли решить ее, а из тех, кто решил, делали это с помощью уравнения. К сожалению, их оказалось мало. В вариантах ЕГЭ по математике 11 класса тоже встречаются задачи на проценты, и эти задачи часто вызывают затруднения у школьников. Причина в том, что тема "Проценты" изучается в младших 5-6 классах, причем непродолжительно, закрепляется в 7 классе при решении задач на повторение, а в старших классах к этой теме, совсем не возвращаются.
Поэтому, изучение наиболее часто встречающихся типов задач на проценты, в частности, задач на концентрацию, смеси и сплавы считаю актуальным.
Объектом исследования является изучение различных типов задач по теме «Проценты».
Изучая эту тему, я пришла к мнению, что многие задачи авторы сборников предлагают решать с использованием специальных формул, которых нет в школьных учебниках 5-6 классов, где и изучаются эти темы.
Предмет исследования: решение задач на концентрацию, смеси и сплавы с преимущественным использованием квадрата Пирсона.
Цель работы. Использование квадрата Пирсона для решения задач на концентрацию, смеси и сплавы.
Задачи исследования:
1) Изучить исторический и теоретический материал по интересующему вопросу. 2) Составить практические рекомендации по решению задач концентрацию, смеси и сплавы.
3) Выявить практическое применение таких задач.
4). Определить план дальнейшей работы над темой.
Практическая значимость работы. Данный способ решения задач на концентрацию, смеси и сплавы будет интересен не только школьникам 8 «В» класса, но и выпускникам 9 и 11 класса, которым нужно сдать ЕГЭ в конце учебного года. Здесь они найдут много полезного и интересного.
2. Задачи на смеси и сплавы
В «Занимательной алгебре» Я.И. Перельмана есть любопытная задача под названием «В парикмахерской»
Задача
Может ли алгебра понадобиться в парикмахерской? Оказывается, такие случаи бывают. Мне пришлось убедиться в этом, когда однажды в парикмахерской подошел ко мне мастер с неожиданной просьбой:
-Не поможете ли нам разрешить задачу, с которой мы никак не справимся?
- Уж сколько раствора испортили из-за этого! - добавил другой
- в чем задача?
- У нас имеется два раствора перекиси водорода: 30%- ный и 3 % -ный. Нужно их смешать так, чтобы составился 12% -ный раствор. Не можем подыскать правильной пропорции…
Мне дали бумажку, и требуемая пропорция была найдена.
Она оказалась очень простой. Какой именно?
РЕШЕНИЕ
Задачу можно решить и арифметически, но язык алгебры приводит здесь к цели проще и быстрее. Пусть для составления 12%-ной смеси требуется взять x граммов 3%-ного раствора и y граммов 30% -ного раствора. Тогда в первой пропорции содержится 0,03x граммов чистой перекиси водорода, во второй 0,3y, а всего
0,03x + 0,3y
В результате получается (x + y) граммов раствора, в котором чистой перекиси должно быть 0,12 (x + y)
Имеем уравнение
0,03x + 0,3y=0,12 (x + y)
Из этого уравнения находим x =2y, т.е. 3%-ного раствора надо взять вдвое больше.
Задача, описанная Перельманом встречается не только в парикмахерских.
Например, для зарядки аккумуляторов бывает необходимо приготовить электролит, который должен содержать 24% серной кислоты из двух растворов с содержанием 92% и 10% серной кислоты. На консервных заводах возникает необходимость приготовления 6%-ного уксуса разной крепости: 3% и 10%, и т.д.
Старинный способ решения задач.
Старинный способ решения задач на смешение двух веществ позволяют получить правильный ответ.
Предположим, что смешиваются два вещества – первое стоимостью, а гривен за фунт и второе стоимостью b гривен за фунт. Желательно получить вещество стоимостью с гривен за фунт. Будем считать, что, а <b
(если с> b или c <a, то задача неразрешима, ибо, смешивая дешевые вещества, дорогое не получишь).
Поэтому можно считать, что a <c <b.Смешиваем один фунт первого вещества и q второго. В результате получится 1+q фунтов вещества стоимостью a+bq гривен. Один фунт смеси должен стоить с гривен. Значит должно выполняться равенство a+bq=c*(1+q). Отсюда находим q=(c-a) /(b-c) или (b-c):(c-a).
Именно этот соотношение дает старинный способ


 a b - c
a b - c
c
b c – a
1.У некоторого человека были продажные масла: одно ценою 10 гривен за ведро, а другое 6 гривен за ведро. Захотелось ему сделать из этих двух масел, смешав их, масло ценою 7 гривен за ведро. Какие части этих двух масел нужно взять, чтобы получить ведро масла стоимостью 7 гривен?
Решение:
Друг над другом пишутся стоимости имеющихся масел, слева от них и примерно посередине – стоимость масла, которое должно получиться после смешения. Соединив записанные числа черточками, получим такую картину:
 6
6
7
10
Меньшую цену вычтем из цены смешанного масла и результат и поставим справа от большей цены. Затем из большей цены вычтем цену смешанного масла и запишем справа от меньшей цены. Получим такую картину:


 6 3
6 3
7
10 1
Делается заключение, что дешевого масла нужно взять втрое больше, чем дорогого, т.е. для получения одного ведра масла стоимостью 7 гривен нужно взять дорогого масла ¼ ведра, а дешевого -3/4 ведра. (Проверка:1/4*10 +3/4*6 = 28/4=7гривен)
2. Некто имеет серебро разных проб: одну- 12 пробы, другое -10 пробы, третье -6 пробы. Сколько, какого серебра надо взять, чтобы получить 1 фунт серебра 9 пробы?
Решение: запишем схематически




 6 3 3+1=4
6 3 3+1=4
9
12 3


 6 1
6 1
9
10 3
Отсюда следует, что надо взять 4 /10 фунта серебра 6 пробы, 3 /10 фунта серебра 10 пробы и 3/ 10 фунта серебра 12 пробы
3. Имеет некто чай 3х сортов – цейлонский по 5 гривен за фунт, индийский по 8 гривен за фунт и китайский по 12 гривен за фунт. В каких долях нужно смешать эти три сорта, чтобы получить чай по 6 гривен за фунт?
Вот решение из «Арифметики» Л. Ф. Магницкого: «А когда случится мешати три товара из них же сделати четвертый по желаемой цене и тогда един перечень малейший дважды в правиле полагается. Яко же здесь видимо есть:


 5 6 6 +
5 6 6 +
 6
6 ![]()
![]()
12 1
+


 5 2 1 +
5 2 1 +
 6
6 ![]()
![]()
8 1
Здесь предлагается взять 6+2= 8 частей чаю ценою по 5 гривен и по одной части чая ценною 8 гривен и 12 гривен за фунт.
Указанный Л. Ф. Магницким способ состоит в следующем. Надо дважды применить способ записи исходных данных и необходимых количеств веществ, причем в первый раз взять вещества с большей и меньшей стоимостью, а во второй раз с наименьшей и средней стоимостью. Повторив действие вычитания и соответствующей записи разности, получим доли, в которых нужно смешивать вещества наибольшей и средней стоимости (на соответствующих строках). Сложив доли дешевого вещества, найденные в первый и во второй раз, получим долю дешевого вещества в общей смеси.
4. Имеется серебро: одно 11 пробы, а другое 14 пробы. Сколько, какого серебра надо взять, чтобы получить 1 фунт серебра 12 пробы?
11 2
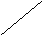
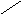

1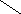 2
2
14 1
2/3 фунта серебра 11 пробы и 1/3 фунта серебра 14 пробы/
В России существовала золотниковая система обозначения пробы на основе русского фунта, содержащего 96 золотников, по которой проба выражалась весовым количеством благородного металла в 96 единицах сплава, например, слова «серебро 11 пробы» означают, что в 96 частях сплава содержится 11 частей серебра.
В наше время проба обозначает число частей благородного металла в 1000 частях (по массе) сплава.
Задачи на смешение трех веществ могут иметь не единственное решение.
Предположим, что смесь, составленная из а фунтов цейлонского чая, b фунтов индийского чая и c фунтов китайского чая имеет цену 6 гривен за фунт. Тогда
5 a+ 8b+12c = 6 или a=6c+2b
a+ 8b+12c = 6 или a=6c+2b
a+b+c
Значит, эта смесь может быть получена соединением смесей 1 (цейлонский и китайский в отношении 6:1) и 2 (цейлонский и китайский в отношении 2:1), в отношении с: b.
Квадрат Пирсона
Для решения подобных задач удобно пользоваться «квадратом Пирсона». Вот как это делается. Рисуют квадрат и проводят две диагонали. (рис. 1) В левом верхнем углу проставляют больший показатель крепости исходных веществ (а), а в нижнем углу-второй показатель(b) а на пересечении диагоналей записывают требуемый показатель (с).
Затем производят вычитание по первой диагонали (а - с) и находят количество второй части (у). Из центра производят вычитание по второй диагонали (c - b) и находят количество первой части смеси (x). Значения x и y записывают по одной линии с показателями. На x частей первого вещества надо взять y частей второго вещества, тогда получится смесь с показателем с.
c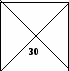 a
a 
 x 36 12
x 36 12
b y 6 18
Рис .1 Рис.2
Пусть, например, имеются две партии сливок: одна содержит 36% жира, а другая -18%. Требуется определить, сколько надо взять и тех, и других сливок, чтобы получить смесь с количеством жира 30%. Решаем по изложенному выше способу (рис.2) и получаем
y=a – c = 36 – 30 = 6
x=c – b =30 – 18 = 12
то есть на 6 массовых частей второй партии надо взять 12 частей первой.
Этот способ основан на специфическом виде количества получаемой смеси, оно равно разности показателей исходных веществ. Такое допущение вполне возможно, так как нас интересуют не абсолютные величины, а относительные количества двух частей смеси.
В самом деле, мы получаем:
x + y = (c – b) + (a + c) = a – b
частей смеси. «Чистого» вещества в ней будет
![]() частей,
частей,
а крепость смеси будет равна 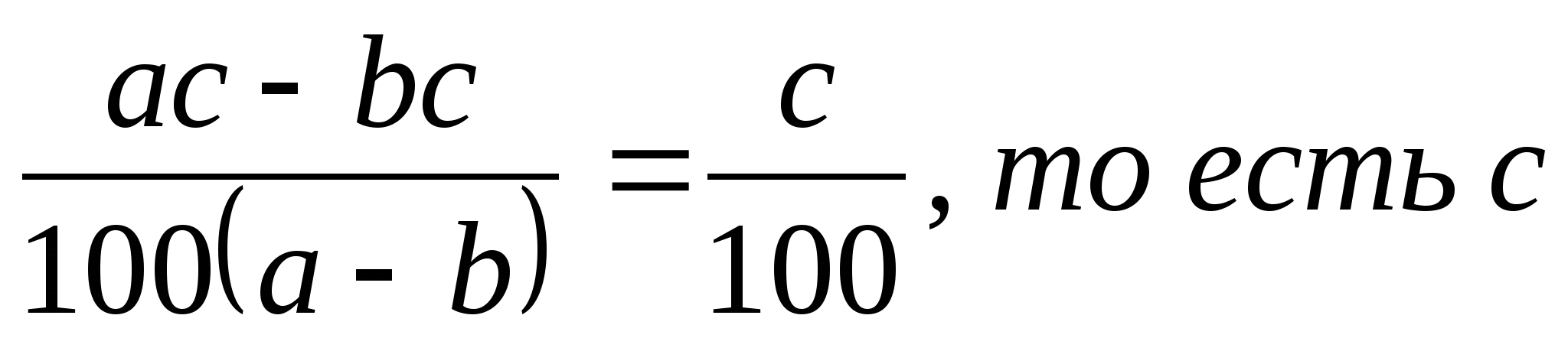 %
%
Решение задач
Данный тип задач охватывает большой круг ситуаций – смешение товаров разной цены, жидкостей с различным содержанием соли, кислот различной концентрации, сплавление металлов с различным содержанием некоторого металла и пр. Связь различных задач между собою станет яснее, если рассматривать типичные ситуации в общем виде. При решении задач данного типа используются следующие допущения:
1.Всегда выполняется «Закон сохранения объема или массы»: если два раствора (сплава) соединяют в «новый» раствор (сплав), то выполняются равенства:
V = V1+V2 –сохраняется объем;
m = m1 + m2 – закон сохранения массы.
2.Данный закон выполняется и для отдельных составляющих частей (компонентов)сплава (раствора).
3. При соединении растворов и сплавов учитываются химические взаимодействия их отдельных компонентов.
Задачи на смеси, растворы и сплавы называют еще задачами на процентное содержание или концентрацию. Введем основные понятия. Говоря о смесях, растворах и сплавах, будем употреблять термин «смесь» независимо от ее вида (твердая, жидкая, газообразная, сыпучая и т.д.). Смесь состоит из «чистого вещества» и «примеси». Долей, а чистого вещества в смеси называется отношение количество чистого вещества m в смеси к общему количеству М смеси при условии, что они измерены одной и той же единицей массы или объема: а = m/М. Отсюда получаем m = aM, M =m/a. Понятие доли чистого вещества можно вводить следующей условной записью:
Доля чистого вещества в смеси равна количеству чистого вещества в смеси, деленному на общее количество смеси. Заметим, что складывать и вычитать доли и процентные содержания нельзя.
Процентным содержанием чистого вещества в смеси с называют его долю, выраженную процентным отношением: с = а100%, а = с/100%.
Считаем полезным предложить школьникам формулу, по которой рассчитывают концентрацию смесей (сплавов):
n = mв /mp,
где n – концентрация,
mв - масса вещества в растворе (сплаве),
mp – масса всего раствора (сплава).
Задача 1.
Сколько граммов воды надо добавить к 50 г раствора, содержащего 8 % соли, чтобы получить 5 % раствор?
Решение.
1 способ (алгебраический)
Пусть x количество воды, которое надо добавить. Новое количество раствора – (50 + x) г. Количество соли в исходном растворе 50 0,08 г. Количество соли в новом растворе составляет 5 % от (50 + x) г, т.е. 0,05 (50 + x) г.
Так как количество соли от добавления воды не изменилось, то оно одинаково в исходном и новом растворах. Получаем уравнение. Иногда в химии это уравнение называют кратко «баланс соли».
50* 0,08 = 0,05* (50 + x)?
50* 8= 5* (50 + x),
80 = 50 + x,
x = 30.
Ответ: 30 г.
2 способ (арифметический)
8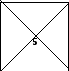
 (50 г) 8 5
(50 г) 8 5
0 ? г 0 3
Значит, всего надо взять 5/8 солевого раствора и 3/8 воды.
1 часть составляет 10 г, значит 3 части содержат 30 г
Ответ: 30 г.
Задача 2
Сколько граммов 30 % - го раствора надо добавить к 80 г 12 % раствора этой же соли, чтобы получить 20 % раствор соли?
Решение.
1 способ (алгебраический)
Пусть надо добавить x u 30 % раствора соли. Получится (80 + x) г 20 % раствора. В 80 г 12 % раствора содержится 80*0,12 г соли 0,3x г соли – в x г 30 % раствора, 0,2* (80 + x) г 20 % раствора.
Получаем уравнение:
0,3 x + 0,12*80 = 0,2* (80 + x) – это и есть «баланс по соли».
0,3 x + 9,6 = 16 + 0,2 x,
0,3 x – 0,2 x = 16 – 9,6,
0,1 x = 64,
X = 64.
Ответ: 64 г.
2 способ (арифметический)
3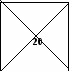 0 8 ( ?г)
0 8 ( ?г)
12 10 (80г)
Значит, всего надо взять 8/18 30% раствора и 10/18 12% раствора.
1 часть составляет 8 г, значит 8 частей содержат 64 г
Ответ: 64 г.
Задача 3.
Имеются два раствора 68% и 78%- ной серной кислоты. Сколько надо взять каждого раствора, чтобы получить 100 г.70% -ного раствора серной кислоты?



 70 68 8
70 68 8
78 2
Надо взять 80 г. 68% кислоты и 78%-ного раствора серной кислоты.
Задача 4.
Имеется два куска олова и свинца, содержащие 60 % и 40 % олова. По сколько граммов от каждого куска надо взять, чтобы получить 600 г сплава, содержащего 45 % олова?
Решение.
1 способ (алгебраический)
Пусть масса куска, взятого от первого сплава m1 г, тогда масса куска от второго сплава будет 600 – m1, составим уравнение
m1 0,6 +(600 – m1)0,4 = 600*0,45,
6 m1 +2400 - 4 m1 = 2700,
20 m1 = 3000, m1= 150,
600 – m1 = 450,
m 2 = 450.
Ответ: 150 г; 450.
2 способ (арифметический)
6 0 5 (?г)
0 5 (?г)
40 15(?г)
Значит, всего надо взять 5/20 60% сплава и 15/20 40% сплава.
1 часть составляет 30 г, значит 5 частей содержат 150 г, а 15 частей – 450г.
Ответ: 150г и 450г
Заключение.
В ходе работы мы изучили исторический и теоретический материал по интересующему вопросу. Составили практические рекомендации по решению задач концентрацию, смеси и сплавы. Выявили практическое применение таких задач. Хотим научиться решать с помощью квадрата Пирсона более сложные задачи, в том числе и олимпиадные.
Помните, с чего мы начали разговор?
Имеются два сплава с разным содержанием золота. В первом сплаве содержится 30%, а во втором 55% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?
3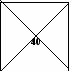 0 15
0 15
55 10
Значит, первый и второй сплавы находятся в отношении 15:10 или 3:2.
Ответ: 3:2.
Теперь моим одноклассникам не составляет труда решать такого рода задачи.
Значимость данной работы
При решении задач мы пришли к выводу, что:
А) Использование квадрата Пирсона позволяет экономить время на ЕГЭ.
Б) Наша работа может быть использована для проведения практических занятий на элективных курсах с учащимися выпускных классов и при подготовке к Единому Государственному Экзамену.
Литература
Перельман Я.И.Занимательная алгебра
Азия А., Вольпер И. Квадрат Пирсона. - М., Квант, № 3/73. С. 61.

| Автор | |
|---|---|
| Дата добавления | 09.12.2019 |
| Раздел | Алгебра |
| Подраздел | Научная работа |
| Просмотров | 1810 |
| Номер материала | 6471 |