Презентация к уроку " Одночлен и его стандартный вид"

Пусть кто-нибудь попробует  вычеркнуть из математики степени, и он увидит, что  без них далеко не уедешь. М.В. Ломоносов

Решите ребус ОД(И)Н ОЧ(КИ) ЛЕН(ТА) ОДНОЧЛЕН

Тема урока. Одночлен и его стандартный вид

При решении различных задач часто встречаются алгебраические выражения вида a · b; 2 · a· b · c; 3 · a2 · b. Для сокращения записи этих выражений знак умножения «точка» обычно опускается, то есть пишут просто ab; abc; 3a2b. Каждое из этих произведений называют одночленом.

ОДНОЧЛЕНОМ НАЗЫВАЕТСЯ АЛГЕБРАИЧЕСКОЕ ВЫРАЖЕНИЕ, КОТОРОЕ ПРЕДСТАВЛЯЕТ СОБОЙ ПРОИЗВЕДЕНИЕ ЧИСЕЛ И ПЕРЕМЕННЫХ, ВОЗВЕДЕННЫХ В СТЕПЕНЬ С НАТУРАЛЬНЫМИ ПОКАЗАТЕЛЯМИ. 0; 2; -0,6; x; а; в; одночлены х5 ; у7

Одночлены

Являются ли одночленами следующие выражения ?

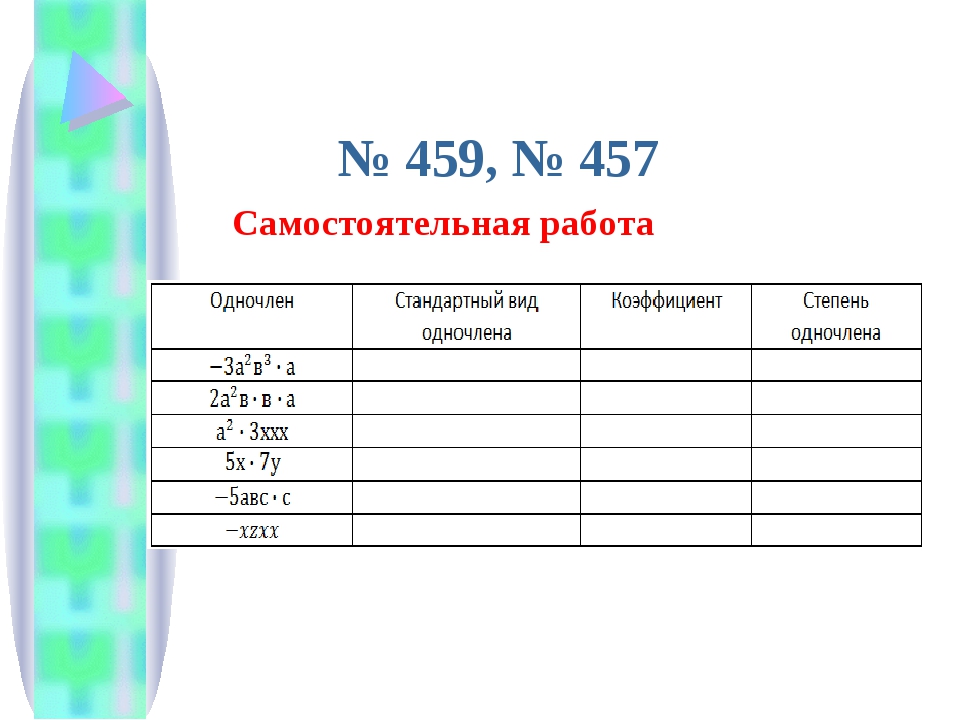
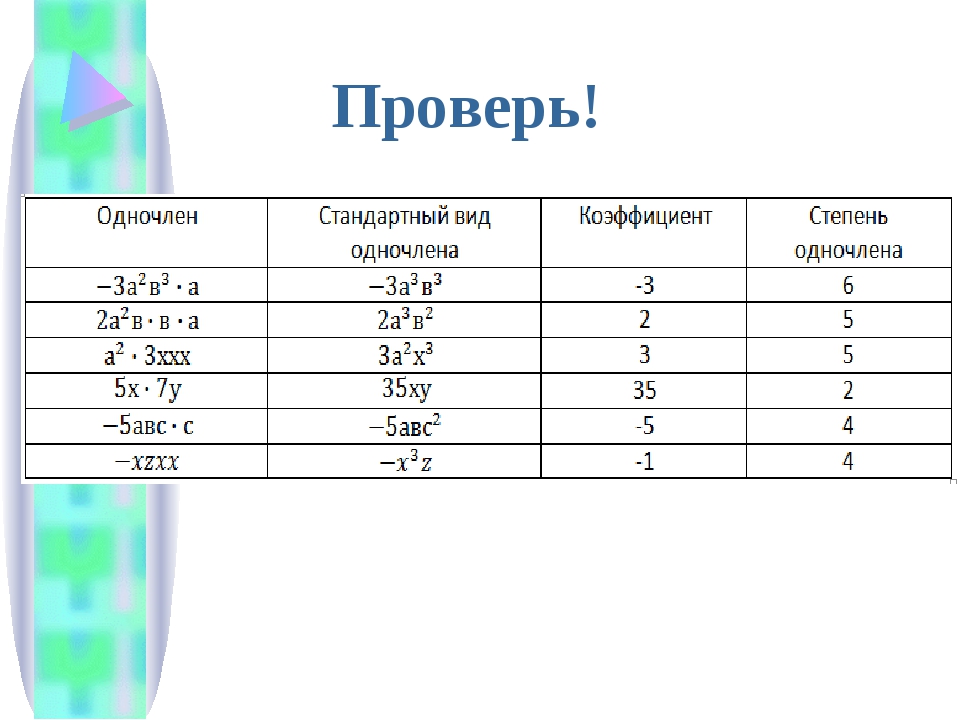
Одночлены стандартного вида Одночлены нестандартного вида Одночлен, в котором единственный числовой множитель стоит на первом месте и степень любой переменной входит множителем только один раз, называется одночленом стандартного вида.

Любой одночлен можно привести к стандартному виду!

Алгоритм приведение одночлена к стандартному виду: Перемножить все числовые множители и поставить их произведение на первое место; Перемножить все имеющиеся степени с одним буквенным основанием; Перемножить все имеющиеся степени с другим буквенным основанием и т.д.

Привести одночлен к стандартному виду: а) 3x2yz*(-2)xy2z5 = 3*(-2)x2xyy2zz5 = = -6x3y3z6 b)-2ax2y3zn * 0,5ax5yz = - 2*0,5aax2x5y3yznz= = - a2x7y4zn+1

Работаем устно: Приведите одночлен к стандартному виду:

Коэффициент одночлена Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.

Степень одночленов Степенью одночлена называют сумму показателей степеней всех входящих в него переменных. 7а1х2у3 – степень равна 1+2+3 = 6 -9с4е3 – степень равна 4+3 = 7 Если одночлен не содержит переменных (т.е. является числом), то его степень считают равной нулю. 24 – степень равна 0

Запишите стандартный вид следующих одночленов и подчеркните коэффициент одной чертой, а буквенную часть волнистой линией. 3ххууу = 2) 2d . 2ссс = 3) ах . ах . ах = Если коэффициент одночлена равен 1 или -1, такой коэффициент обычно не пишут, но подразумевают.

Работаем устно: Определите степень одночлена:

№ 459, № 457 Самостоятельная работа

Проверь!

С какими новыми понятиями вы познакомились на уроке? Одночлен Алгоритм Деление Стандартный вид Коэффициент