
Презентация "Арксинус. Решение уравнения sint = a"

Краткое описание документа:
Презентация посвящена теме «Арксинус. Решение уравнения sint = a». В ней будет рассмотрено такое понятие, как арксинус и будут выведены методы решения уравнений типа sint = a.
Материал является четко структурированным и грамотно составленным. Он включает в себя небольшое количество слайдов, с помощью которых изучение одной из тем из области геометрии станет намного эффективным.
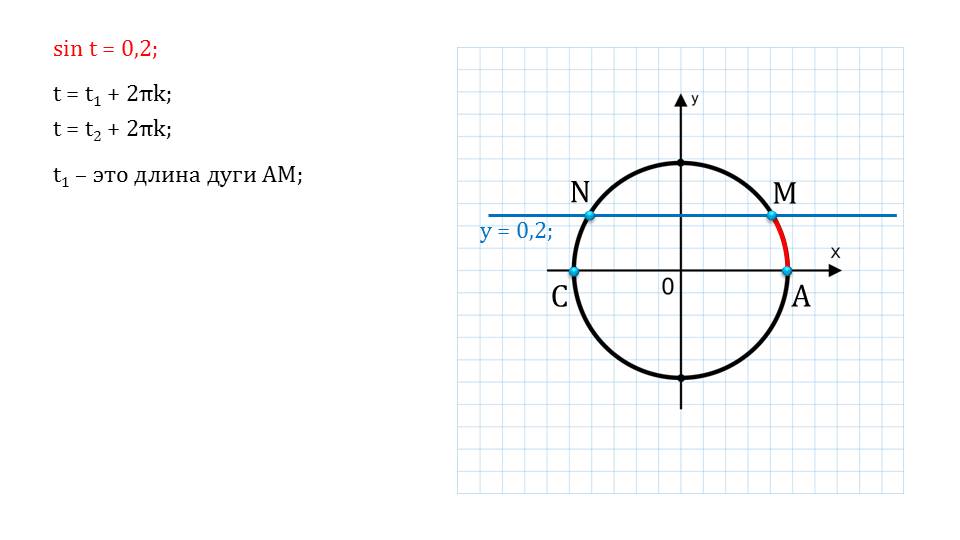
Начинается презентация с примера уравнения.
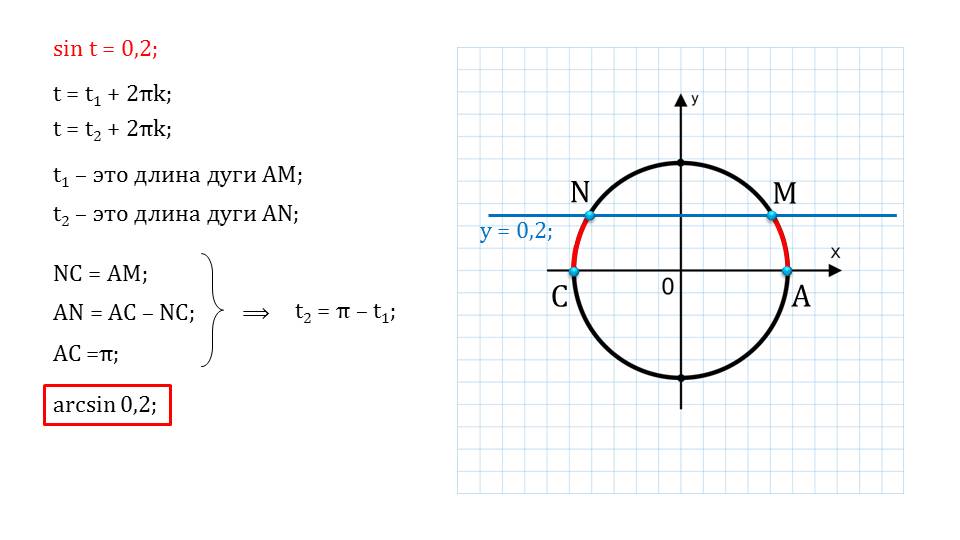
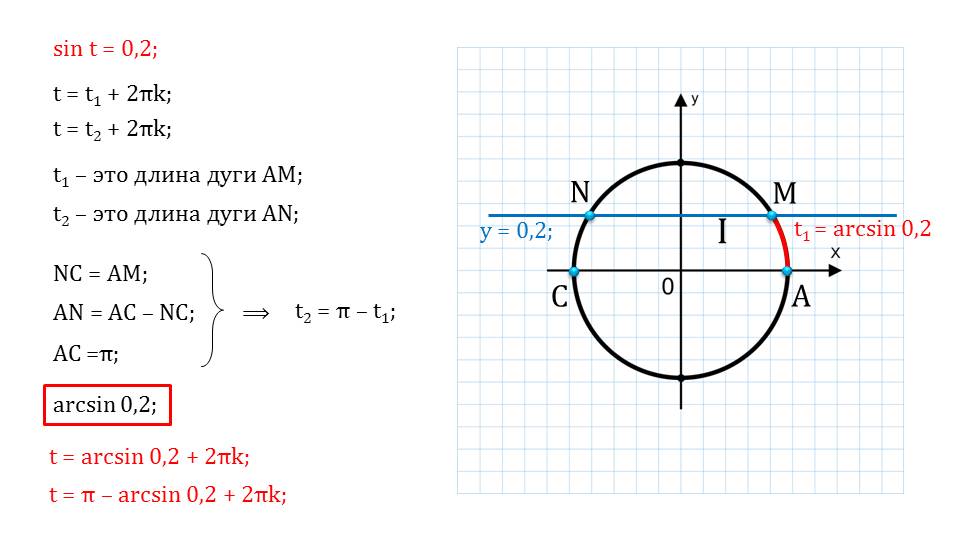
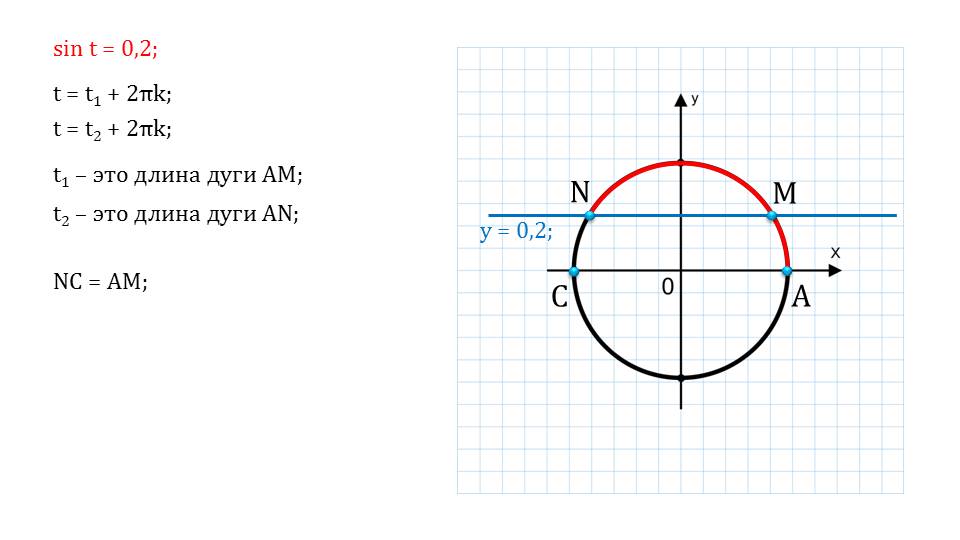
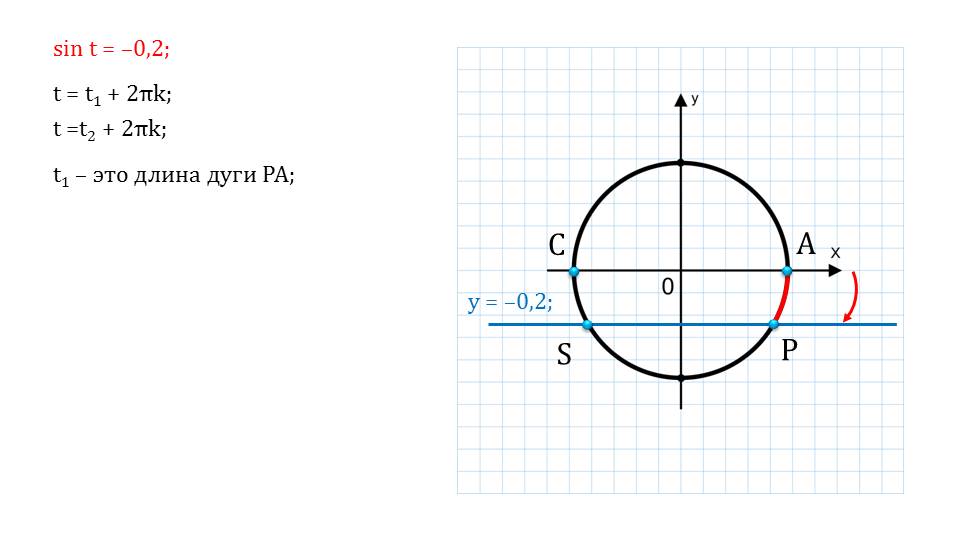
В левой части мы видим синус некоторого значения, а в правой – десятичное число. Также мы видим иллюстрацию, на которой показывается геометрическое решение. С помощью дополнительных построений можно найти множество корней уравнения. Показывается геометрический смысл арксинуса, что важно знать.
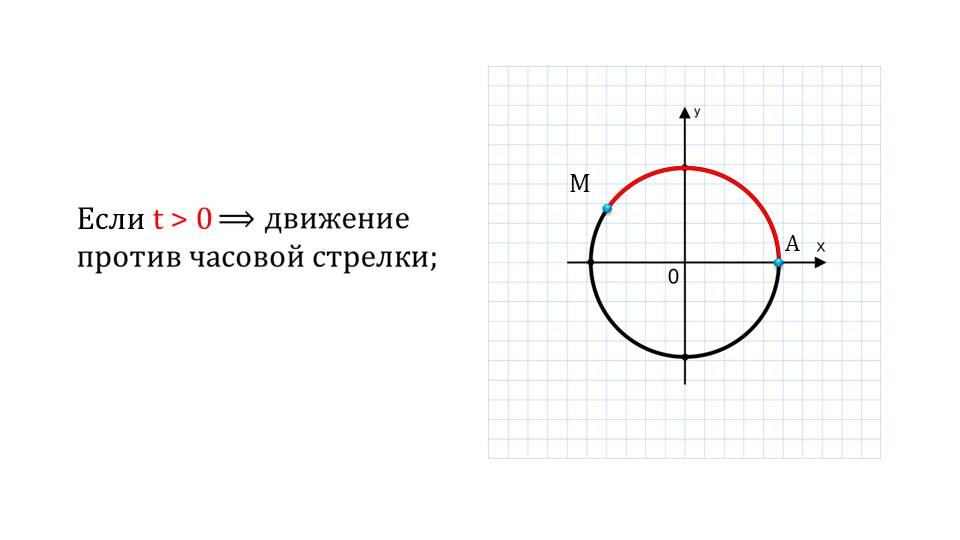
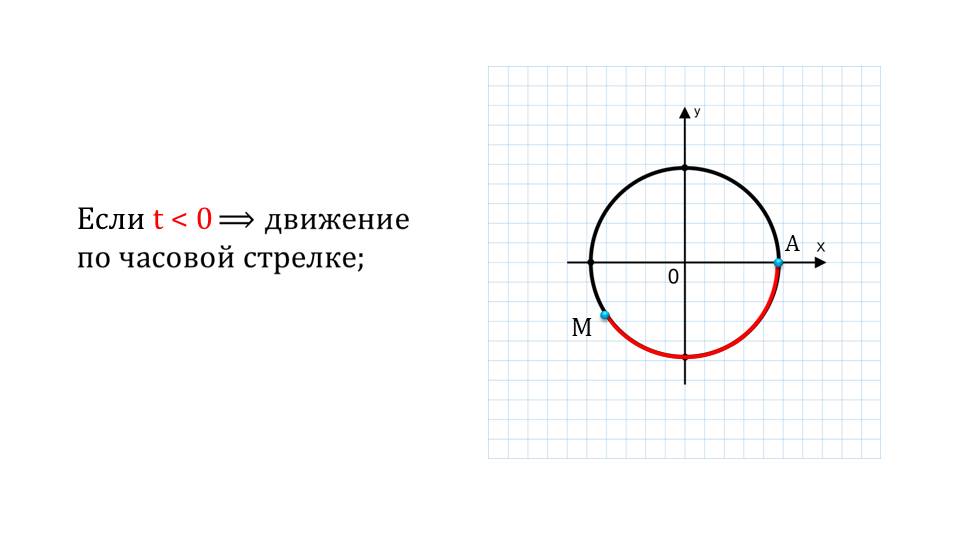
На следующем слайде показывается, каким образом будет меняться решение уравнения при знаке аргумента. Если аргумент будет больше нуля, то движение пойдет против часовой стрелки, если меньше – то по часовой стрелке. В случае равенства нулю решением будет являться начальная точка и движения не произойдет.
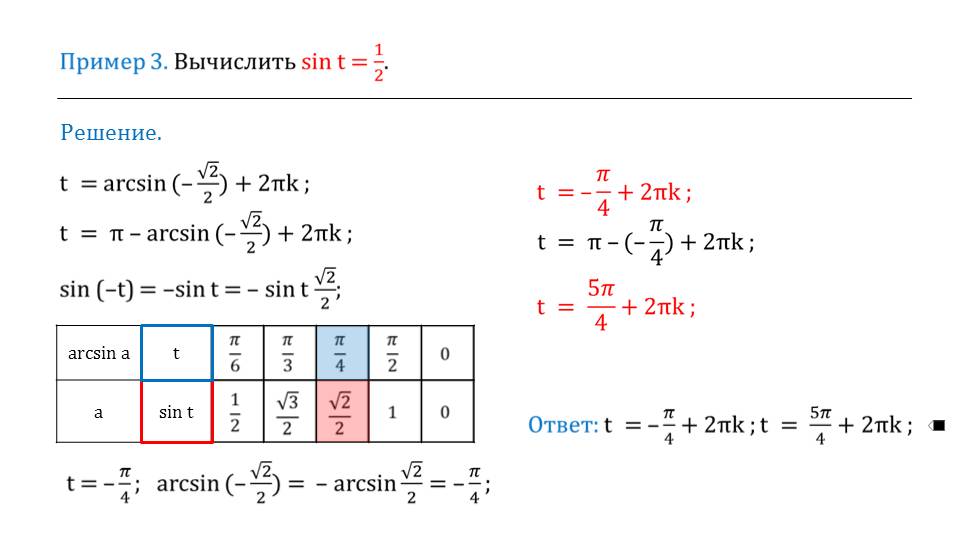

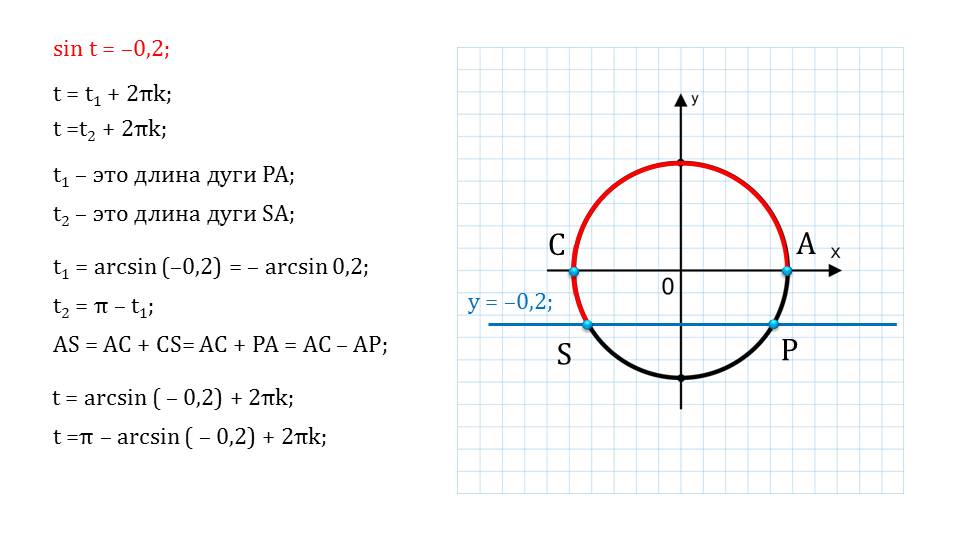
Далее приводится еще один пример, где аналогичным образом показывается геометрическое решение. Если переменная, стоящая под арксинусом, будет по модулю меньше либо равно единице, то арксинусом данного числа будет называться некоторое значение из определенного интервала, синус которого равен нулю.
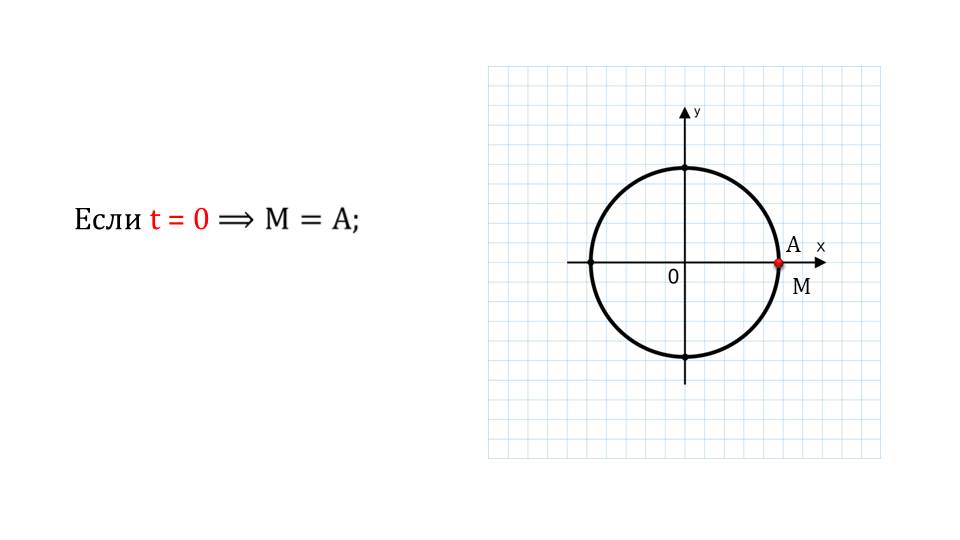
Этот отрезок, то есть интервал, обозначен красным цветом в определении. Для того чтобы найти решение уравнения sint = a при а по модулю меньше либо равно единице, необходимо знать общий вид решения, который выводится на слайде.

Решения некоторых часто встречаемых уравнений приводятся на следующем слайде. С левой стороны мы видим равенства 0, 1 и -1, а с правой стороны их решения, выделенные красным цветом.
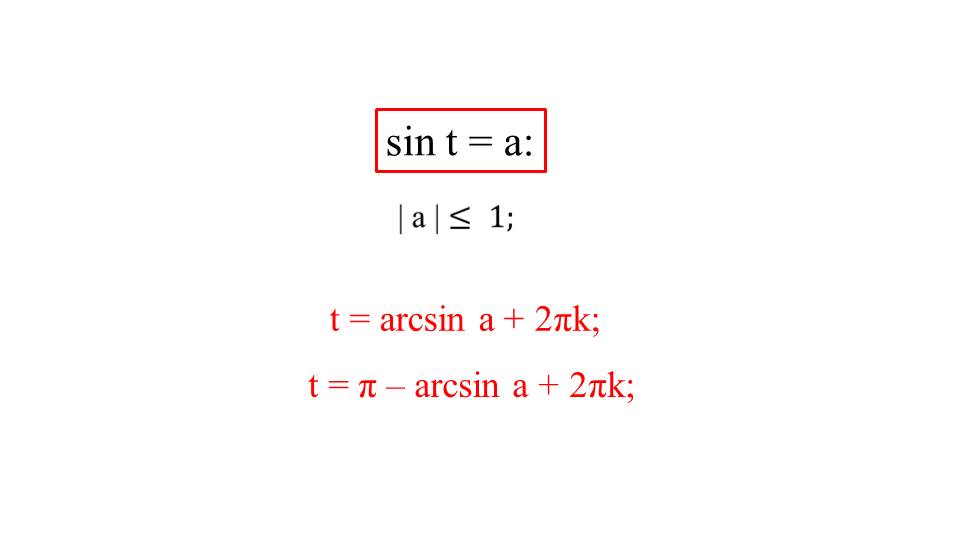
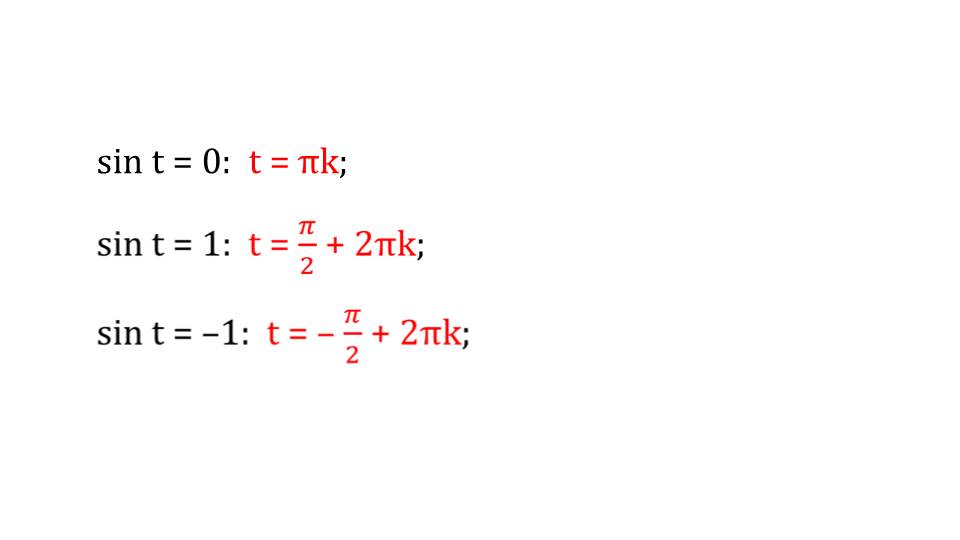
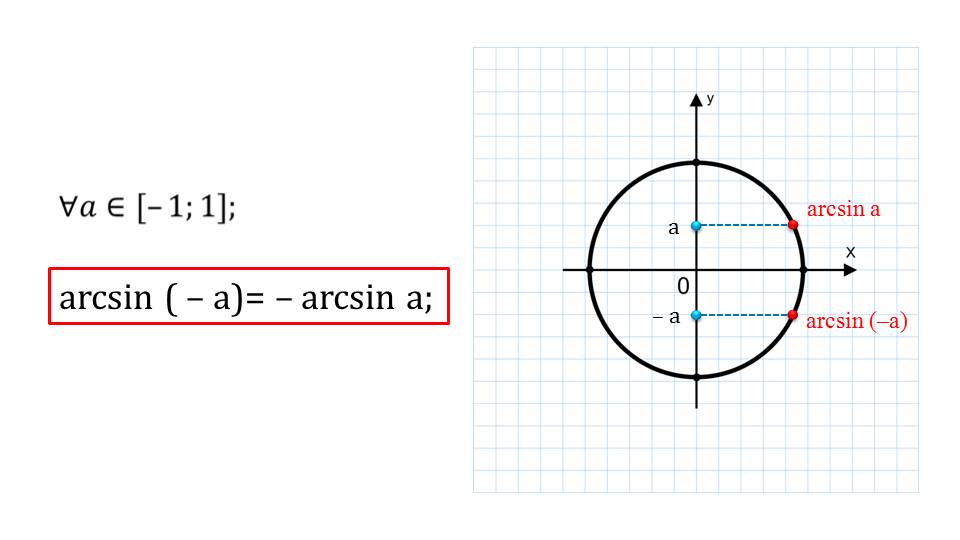
В случае принадлежности а от -1 до 1 выполняется некоторое правило: минус, стоящий при аргумента, можно вынести.
Далее предлагается рассмотреть примеры.
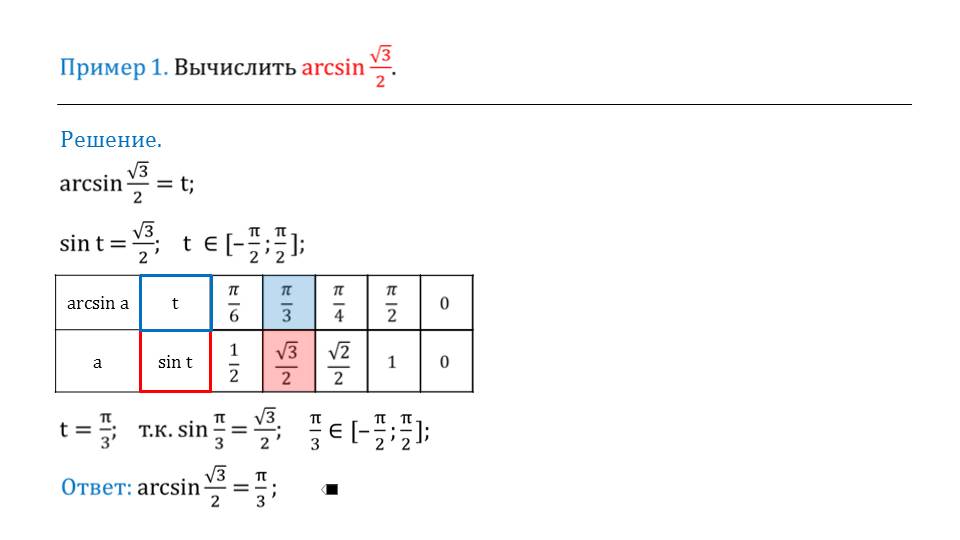
В первом из них предлагается найти арксинус некоторого числа, которое представляет собой дробь. Решение приводится поэтапно. При его выполнении мы обращаемся к таблице, с которой ранее школьники должны были иметь дело.
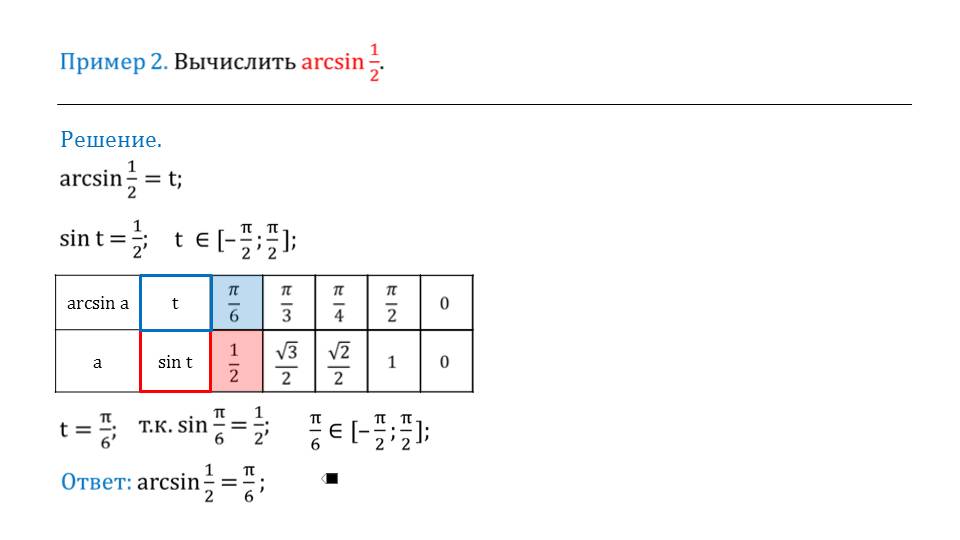

Все обоснования приведены понятным и подробным образом. Данный пример желательно рассмотреть вместе с учителем. Второй пример предлагает посчитать арксинус ½.

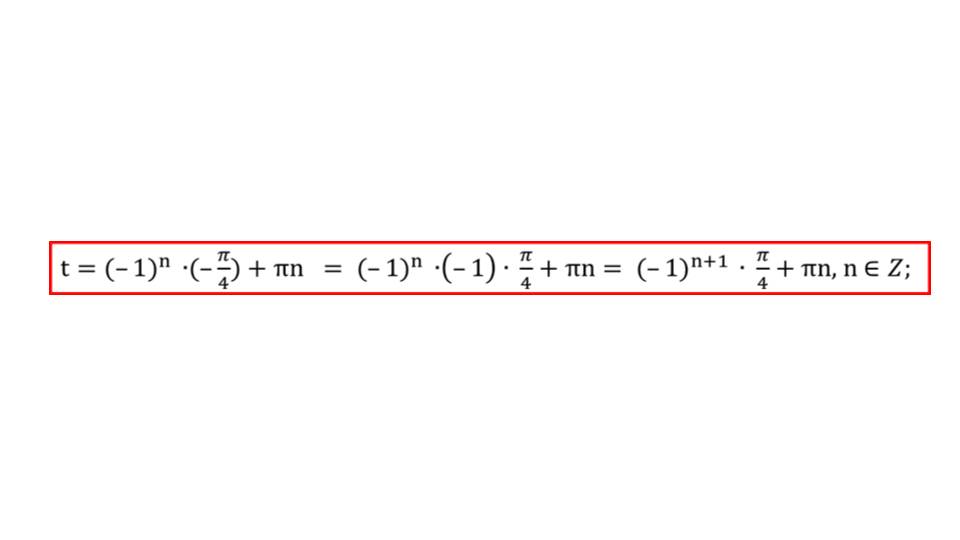
Прежде, чем показать слайд школьникам, можно предложить им решить пример самостоятельно. После чего, можно продемонстрировать им решение, с которым они могли бы сравнить ответ.
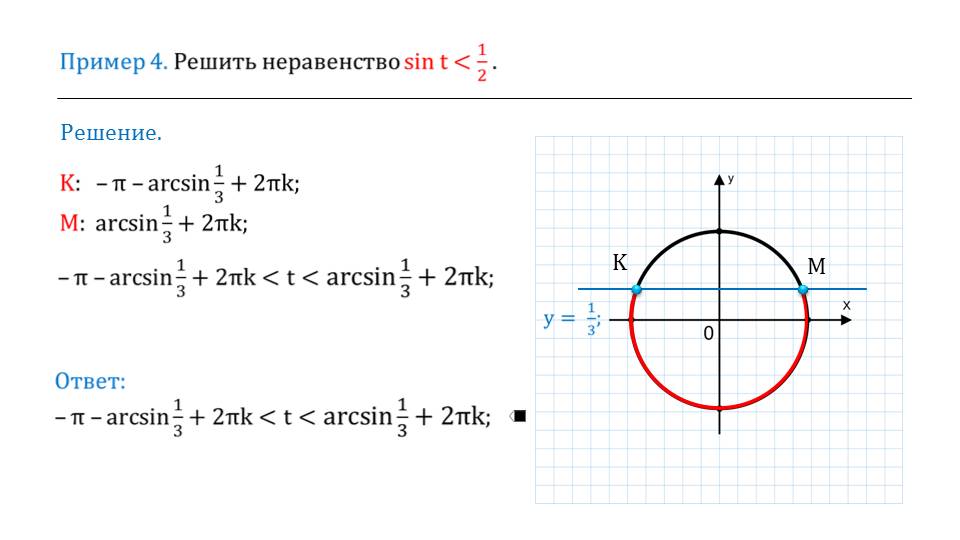

На следующем слайде приводятся свойства арксинуса, которые необходимо рассмотреть в ходе данного урока. Следующие примеры, которые рассматриваются в презентации, представляют собой решения неравенств. Их решения очень грамотно составлены и дополнены анимационными эффектами, с помощью которым станут ясны школьникам.

Последующие примеры достаточно объемны и сложно, однако, их рассмотрение является необходимым.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4277 |
| Номер материала | 807 |